顺时针打印矩阵题解（文末附完整代码，自己敲#include这句 和最后return 0 后面的空格中也有不能识别的字符 删掉就行了）

分析：

1.人为的感觉是螺旋形地打印数字，但是，计算机只能一行一行地打印数字，所以想到：

先创建二维数组（最好是变长数组）来存放这些数，然后再打印。

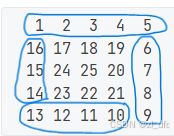
如上图：

上横：一圈螺旋之中，上面一行 的 所有数

右竖：一圈螺旋之中，右边一列 除去顶端之后 的 所有数

下横：一圈螺旋之中，下边一行 除去最右边之后 的 所有数

左竖：一圈螺旋之中，左边一列 除去首尾 的 所有数

2.所谓螺旋：先是“上横”这一行数，再是“右竖”这一列数，再是“下横”这一行数，再是“左竖”这一列数......如此循环，所以想到：分别设计好，上横、右竖、下横、左竖 的程序 ，再循环即可。 

---------------------------------------------------------------------------------------------------------------------------------

1.先把套路写好：

#include 
int main ()
{
   int n;
   scanf("%d", &n);
   int a[n][n];

  return 0;
}

​

2.数字从 1 开始直到 n*n ，我们就是把这些数 一个一个 放进二维数组， 所以把这当作

循环结束条件。当然，数组的行列下标也应该先准备好。不知道循环总次数，直接while循环

#include 
int main ()
{
   int n;
   scanf("%d", &n);
   int a[n][n];
   
  int num = 1;
  int hang = 0;
  int lie = 0;
  
  while(num <= n*n)
{

}


  return 0;
}

3.先是“上横”  

#include 
int main ()
{
   int n;
   scanf("%d", &n);
   int a[n][n];
   
  int num = 1;
  int hang = 0;
  int lie = 0;
  
  while(num <= n*n)
{

    //上横
   for(int i = lie; i <= n-1-lie; ++i)
    {
     a[hang][i] = num;
      num++;
    }
   //右竖
   //下横
   //左竖

  ++hang;
  ++lie;

}
  return 0;
}
​

1）首先我们要明白，螺旋一圈之后， 行数列数都要加一， 因为更向内蜷缩了

2）一圈螺旋之中填进“上横”中的数所在的行的位置相同，

所以数组的 行下标 是 hang）（螺旋一圈之后会自增1，正好符合要求

而一圈之中填进“上横”中的数所在的列的位置，

第一圈 列的起始位置是0，螺旋一圈后会更向内蜷缩了，即 会加 1，

所以数组的列下标 i 从 lie 开始， (因为lie初始值为0，螺旋一圈后会自增1，恰好满足我们的要求）

第一圈“上横” 列的结束位置是 n-1，螺旋一圈后会更向内，即 减 1，

所以 i <= n-1-lie  (因为lie初始值为0，螺旋一圈后会自增1，恰好满足我们的要求）

3）将 num 赋值到数组中相应的位置之后 num++，再赋值到下一个位置

4. 然后是“右竖”

#include 
int main ()
{
   int n;
   scanf("%d", &n);
   int a[n][n];
   
  int num = 1;
  int hang = 0;
  int lie = 0;
  
  while(num <= n*n)
{

    //上横
   for(int i = lie; i <= n-1-lie; ++i)
    {
     a[hang][i] = num;
      num++;
    }
   //右竖
   for(int i = hang+1; i <= n-1-hang; ++i)
    {
     a[i][n-1-lie] = num;
      num++;
    }
   //下横
   //左竖

  ++hang;
  ++lie;

}
  return 0;
}
​

1) “上横”中结余的 num 正好就是 “右竖” 中的 我们需要从上往下填入的第一个数（原因见上文“右竖”的定义），赋值之后， ++num;

2）一圈螺旋之中填进“右竖”中的数所在的列的位置不变

第一圈“右竖” 列的位置是 n-1，螺旋一圈后会更向内，即 减 1，

所以数组的列下标是 n-1-lie  (因为lie初始值为0，螺旋一圈后会自增1，恰好满足我们的要求）

而每一圈填进“右竖”中的数所在的行的位置，

需要行数加1（原因见上文“右竖”的定义），即数组的行下标 i 从 hang+1 开始，

第一圈“右竖” 行的结束位置是 n-1，螺旋一圈后会更向内，即 减 1，

所以 i <= n-1-hang  (因为hang初始值为0，螺旋一圈后会自增1，恰好满足我们的要求）

5.然后是下横

​

#include 
int main ()
{
   int n;
   scanf("%d", &n);
   int a[n][n];
   
  int num = 1;
  int hang = 0;
  int lie = 0;
  
  while(num <= n*n)
{

    //上横
   for(int i = lie; i <= n-1-lie; ++i)
    {
     a[hang][i] = num;
      num++;
    }
   //右竖
   for(int i = hang+1; i <= n-1-hang; ++i)
    {
     a[i][n-1-lie] = num;
      num++;
    }
   //下横
   for(int i = n-2-lie; i >= lie; --i)
    {
     a[n-1-hang][i] = num;
      num++;
    }
   //左竖

  ++hang;
  ++lie;

}
  return 0;
}

1) “右竖”中结余的 num 正好就是 “下横” 中的 我们需要从后向前填入的第一个数（原因见上文定义），赋值之后， ++num; 

2）一圈螺旋之中填进“下横”中的数所在的行的位置相同，

第一圈“下横” 行的位置是 n-1，螺旋一圈后会更向内，即 减 1，

数组的行下标 i 为 n-1-hang (因为hang初始值为0，螺旋一圈后会自增1，恰好满足我们的要求）

而一圈螺旋之中填进“下横”中的数所在的列的位置，

第一圈“下横” 列的起始位置是 n-2（原因见上文定义），螺旋一圈后会更向内，即 减 1，所以

 数组的列下标 i从 n-2-lie 开始(因为lie初始值为0，螺旋一圈后会自增1，恰好满足我们的要求）

第一圈“下横” 列的终止位置为 0， 螺旋一圈后会更向内，即 加 1，

所以 数组的列下标 i >= lie 开始(因为lie初始值为0，螺旋一圈后会自增1，恰好满足我们的要求）

5.然后是左竖

​

​

#include 
int main ()
{
   int n;
   scanf("%d", &n);
   int a[n][n];
   
  int num = 1;
  int hang = 0;
  int lie = 0;
  
  while(num <= n*n)
{

    //上横
   for(int i = lie; i <= n-1-lie; ++i)
    {
     a[hang][i] = num;
      num++;
    }
   //右竖
   for(int i = hang+1; i <= n-1-hang; ++i)
    {
     a[i][n-1-lie] = num;
      num++;
    }
   //下横
   for(int i = n-2-lie; i >= lie; --i)
    {
     a[n-1-hang][i] = num;
      num++;
    }
   //左竖
   for(int i = n-2-hang; i >= 1 + hang; --i)
    {
     a[i][lie] = num;
      num++;
    } 

  ++hang;
  ++lie;

}

  return 0;
}
​

1) “下横”中结余的 num 正好就是 “左竖” 中的 我们需要从下往上填入的第一个数（原因见上文定义），赋值之后， ++num; 

2）每一圈螺旋填进“左竖”中的数所在的列的位置相同，

第一圈螺旋“左竖” 列的下标是0，螺旋一圈后会更向内蜷缩，即 加 1，

所以数组的行下标 lie (因为lie初始值为0，螺旋一圈后会自增1，恰好满足我们的要求）

第一圈螺旋“左竖” 行的起始位置是 n-2（原因见上文定义），螺旋一圈后会更向内，即 减 1，所以

 数组的行下标 i 从 n-2-hang 开始(因为hang初始值为0，螺旋一圈后会自增1，恰好满足我们的要求）

第一圈“左竖” 行的终止位置为 1， 螺旋一圈后会更向内蜷缩，即 加 1，

所以 数组的行下标 i >= 1+hang 开始(因为hang初始值为0，螺旋一圈后会自增1，恰好满足我们的要求）

6.最后只需要按要求输出就好啦！！！！

#include 
int main ()
{
   int n;
   scanf("%d", &n);
   int a[n][n];
   
  int num = 1;
  int hang = 0;
  int lie = 0;
  
  while(num <= n*n)
{

    //上横
   for(int i = lie; i <= n-1-lie; ++i)
    {
     a[hang][i] = num;
      num++;
    }
   //右竖
   for(int i = hang+1; i <= n-1-hang; ++i)
    {
     a[i][n-1-lie] = num;
      num++;
    }
   //下横
   for(int i = n-2-lie; i >= lie; --i)
    {
     a[n-1-hang][i] = num;
      num++;
    }
   //左竖
   for(int i = n-2-hang; i >= 1 + hang; --i)
    {
     a[i][lie] = num;
      num++;
    } 

  ++hang;
  ++lie;

}
    for(int i = 0; i < n; ++i)
    {
        for(int j = 0; j < n; ++j)
        {
            printf("%3d", a[i][j]);
        }
        printf("\n");
    }

  return 0;
}
​​