程序员进阶-八大算法攻略
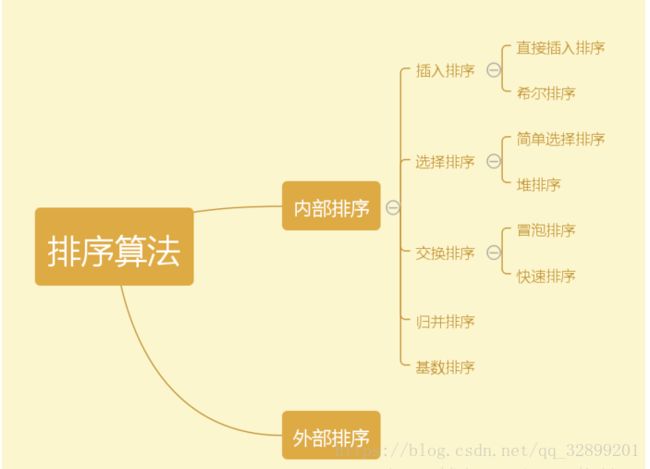
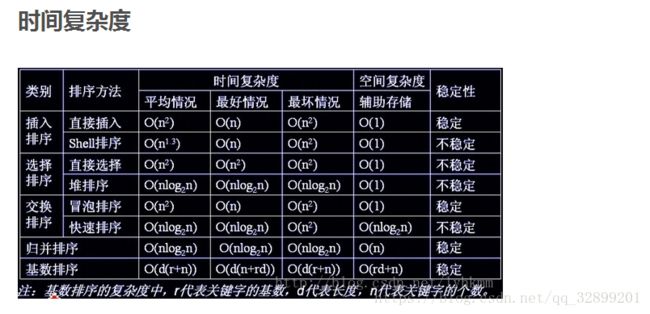
常见的八大排序算法,以及它们之间的关系如下所示:
一、插入排序-直接插入排序
1.算法思想:直接插入排序是一种简单插入排序,基本思想是:把n个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含1个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,将它插入到有序表中的适当位置,使之成为新的有序表,重复n-1次可完成排序过程 。
很简单吧,接下来,我们要将这个算法转化为编程语言。
假设有一组无序序列 R0, R1, ... , RN-1。
(1) 我们先将这个序列中下标为 0 的元素视为元素个数为 1 的有序序列。
(2) 然后,我们要依次把 R1, R2, ... , RN-1 插入到这个有序序列中。所以,我们需要一个外部循环,从下标 1 扫描到 N-1 。
(3) 接下来描述插入过程。假设这是要将 Ri 插入到前面有序的序列中。由前面所述,我们可知,插入Ri时,前 i-1 个数肯定已经是有序了。
所以我们需要将Ri 和R0 ~ Ri-1 进行比较,确定要插入的合适位置。这就需要一个内部循环,我们一般是从后往前比较,即从下标 i-1 开始向 0 进行扫描。
2.核心代码
public void insertSort(int[] list) {
// 打印第一个元素
System.out.format("i = %d:\t", 0);
printPart(list, 0, 0);
// 第1个数肯定是有序的,从第2个数开始遍历,依次插入有序序列
for (int i = 1; i < list.length; i++) {
int j = 0;
int temp = list[i]; // 取出第i个数,和前i-1个数比较后,插入合适位置
// 因为前i-1个数都是从小到大的有序序列,所以只要当前比较的数(list[j])比temp大,就把这个数后移一位
for (j = i - 1; j >= 0 && temp < list[j]; j--) {
list[j + 1] = list[j];
}
list[j + 1] = temp;
System.out.format("i = %d:\t", i);
printPart(list, 0, i);
}
}3.算法时间、空间复杂度、稳定性分析
二、插入排序-希尔排序
1.算法思想:把记录按步长 gap 分组,对每组记录采用直接插入排序方法进行排序。
随着步长逐渐减小,所分成的组包含的记录越来越多,当步长的值减小到 1 时,整个数据合成为一组,构成一组有序记录,则完成排序。
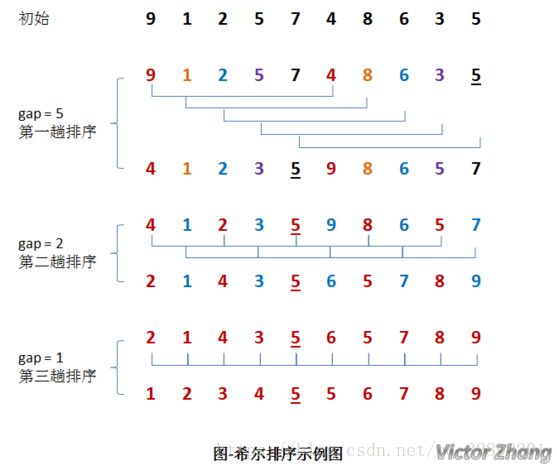
在上面这幅图中:
初始时,有一个大小为 10 的无序序列。
在第一趟排序中,我们不妨设 gap1 = N / 2 = 5,即相隔距离为 5 的元素组成一组,可以分为 5 组。
接下来,按照直接插入排序的方法对每个组进行排序。
在第二趟排序中,我们把上次的 gap 缩小一半,即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组,可以分为 2 组。
按照直接插入排序的方法对每个组进行排序。
在第三趟排序中,再次把 gap 缩小一半,即gap3 = gap2 / 2 = 1。 这样相隔距离为 1 的元素组成一组,即只有一组。
按照直接插入排序的方法对每个组进行排序。此时,排序已经结束。
2.核心代码
public void shellSort(int[] list) {
int gap = list.length / 2;
while (1 <= gap) {
// 把距离为 gap 的元素编为一个组,扫描所有组
for (int i = gap; i < list.length; i++) {
int j = 0;
int temp = list[i];
// 对距离为 gap 的元素组进行排序
for (j = i - gap; j >= 0 && temp < list[j]; j = j - gap) {
list[j + gap] = list[j];
}
list[j + gap] = temp;
}
System.out.format("gap = %d:\t", gap);
printAll(list);
gap = gap / 2; // 减小增量
}
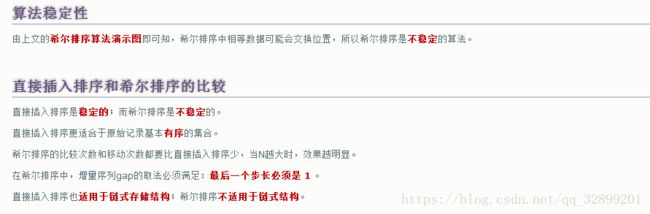
}3.算法时间、空间复杂度、稳定性分析
三、选择排序-简单选择排序
1.算法思想:
(1)从待排序序列中,找到关键字最小的元素;
(2)如果最小元素不是待排序序列的第一个元素,将其和第一个元素互换;
(3)从余下的 N - 1 个元素中,找出关键字最小的元素,重复(1)、(2)步,直到排序结束。
2.核心代码
public void selectionSort(int[] list) {
// 需要遍历获得最小值的次数
// 要注意一点,当要排序 N 个数,已经经过 N-1 次遍历后,已经是有序数列
for (int i = 0; i < list.length - 1; i++) {
int temp = 0;
int index = i; // 用来保存最小值得索引
// 寻找第i个小的数值
for (int j = i + 1; j < list.length; j++) {
if (list[index] > list[j]) {
index = j;
}
}
// 将找到的第i个小的数值放在第i个位置上
temp = list[index];
list[index] = list[i];
list[i] = temp;
System.out.format("第 %d 趟:\t", i + 1);
printAll(list);
}
}3.算法时间、空间复杂度、稳定性分析
四、选择排序-堆排序
1.算法思想:
首先,按堆的定义将数组R[0..n]调整为堆(这个过程称为创建初始堆),交换R[0]和R[n];
然后,将R[0..n-1]调整为堆,交换R[0]和R[n-1];
如此反复,直到交换了R[0]和R[1]为止。
以上思想可归纳为两个操作:
(1)根据初始数组去构造初始堆(构建一个完全二叉树,保证所有的父结点都比它的孩子结点数值大)。
(2)每次交换第一个和最后一个元素,输出最后一个元素(最大值),然后把剩下元素重新调整为大根堆。
当输出完最后一个元素后,这个数组已经是按照从小到大的顺序排列了。
2.核心代码
public void HeapAdjust(int[] array, int parent, int length) {
int temp = array[parent]; // temp保存当前父节点
int child = 2 * parent + 1; // 先获得左孩子
while (child < length) {
// 如果有右孩子结点,并且右孩子结点的值大于左孩子结点,则选取右孩子结点
if (child + 1 < length && array[child] < array[child + 1]) {
child++;
}
// 如果父结点的值已经大于孩子结点的值,则直接结束
if (temp >= array[child])
break;
// 把孩子结点的值赋给父结点
array[parent] = array[child];
// 选取孩子结点的左孩子结点,继续向下筛选
parent = child;
child = 2 * child + 1;
}
array[parent] = temp;
}
public void heapSort(int[] list) {
// 循环建立初始堆
for (int i = list.length / 2; i >= 0; i--) {
HeapAdjust(list, i, list.length);
}
// 进行n-1次循环,完成排序
for (int i = list.length - 1; i > 0; i--) {
// 最后一个元素和第一元素进行交换
int temp = list[i];
list[i] = list[0];
list[0] = temp;
// 筛选 R[0] 结点,得到i-1个结点的堆
HeapAdjust(list, 0, i);
System.out.format("第 %d 趟: \t", list.length - i);
printPart(list, 0, list.length - 1);
}
}3.算法时间、空间复杂度、稳定性分析
五、交换排序-冒泡排序
1.算法思想:假设有一个大小为 N 的无序序列。冒泡排序就是要每趟排序过程中通过两两比较,找到第 i 个小(大)的元素,将其往上排。
以上图为例,演示一下冒泡排序的实际流程:
假设有一个无序序列 { 4. 3. 1. 2, 5 }
第一趟排序:通过两两比较,找到第一小的数值 1 ,将其放在序列的第一位。
第二趟排序:通过两两比较,找到第二小的数值 2 ,将其放在序列的第二位。
第三趟排序:通过两两比较,找到第三小的数值 3 ,将其放在序列的第三位。
至此,所有元素已经有序,排序结束。
要将以上流程转化为代码,我们需要像机器一样去思考,不然编译器可看不懂。
假设要对一个大小为 N 的无序序列进行升序排序(即从小到大)。
(1) 每趟排序过程中需要通过比较找到第 i 个小的元素。
所以,我们需要一个外部循环,从数组首端(下标 0) 开始,一直扫描到倒数第二个元素(即下标 N - 2) ,剩下最后一个元素,必然为最大。
(2) 假设是第 i 趟排序,可知,前 i-1 个元素已经有序。现在要找第 i 个元素,只需从数组末端开始,扫描到第 i 个元素,将它们两两比较即可。
所以,需要一个内部循环,从数组末端开始(下标 N - 1),扫描到 (下标 i + 1)。
2.核心代码
public void bubbleSort(int[] list) {
int temp = 0; // 用来交换的临时数
// 要遍历的次数
for (int i = 0; i < list.length - 1; i++) {
// 从后向前依次的比较相邻两个数的大小,遍历一次后,把数组中第i小的数放在第i个位置上
for (int j = list.length - 1; j > i; j--) {
// 比较相邻的元素,如果前面的数大于后面的数,则交换
if (list[j - 1] > list[j]) {
temp = list[j - 1];
list[j - 1] = list[j];
list[j] = temp;
}
}
System.out.format("第 %d 趟:\t", i);
printAll(list);
}
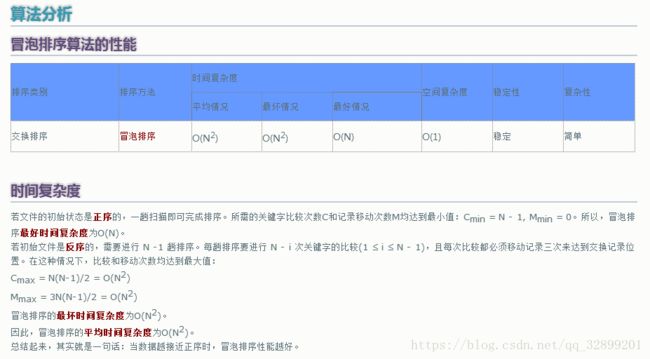
}3.算法时间、空间复杂度、稳定性分析
六、交换排序-快速排序
1.算法思想:
通过一趟排序将要排序的数据分割成独立的两部分:分割点左边都是比它小的数,右边都是比它大的数。
然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
详细的图解往往比大堆的文字更有说明力,所以直接上图:
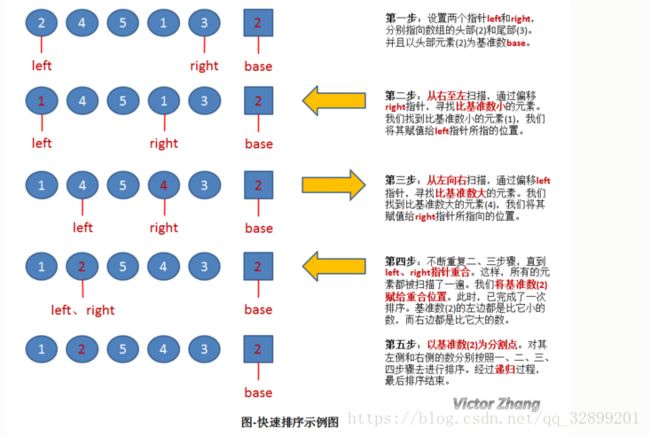
上图中,演示了快速排序的处理过程:
初始状态为一组无序的数组:2、4、5、1、3。
经过以上操作步骤后,完成了第一次的排序,得到新的数组:1、2、5、4、3。
新的数组中,以2为分割点,左边都是比2小的数,右边都是比2大的数。
因为2已经在数组中找到了合适的位置,所以不用再动。
2左边的数组只有一个元素1,所以显然不用再排序,位置也被确定。(注:这种情况时,left指针和right指针显然是重合的。因此在代码中,我们可以通过设置判定条件left必须小于right,如果不满足,则不用排序了)。
而对于2右边的数组5、4、3,设置left指向5,right指向3,开始继续重复图中的一、二、三、四步骤,对新的数组进行排序。
2.核心代码public int division(int[] list, int left, int right) {
// 以最左边的数(left)为基准
int base = list[left];
while (left < right) {
// 从序列右端开始,向左遍历,直到找到小于base的数
while (left < right && list[right] >= base)
right--;
// 找到了比base小的元素,将这个元素放到最左边的位置
list[left] = list[right];
// 从序列左端开始,向右遍历,直到找到大于base的数
while (left < right && list[left] <= base)
left++;
// 找到了比base大的元素,将这个元素放到最右边的位置
list[right] = list[left];
}
// 最后将base放到left位置。此时,left位置的左侧数值应该都比left小;
// 而left位置的右侧数值应该都比left大。
list[left] = base;
return left;
}
private void quickSort(int[] list, int left, int right) {
// 左下标一定小于右下标,否则就越界了
if (left < right) {
// 对数组进行分割,取出下次分割的基准标号
int base = division(list, left, right);
System.out.format("base = %d:\t", list[base]);
printPart(list, left, right);
// 对“基准标号“左侧的一组数值进行递归的切割,以至于将这些数值完整的排序
quickSort(list, left, base - 1);
// 对“基准标号“右侧的一组数值进行递归的切割,以至于将这些数值完整的排序
quickSort(list, base + 1, right);
}
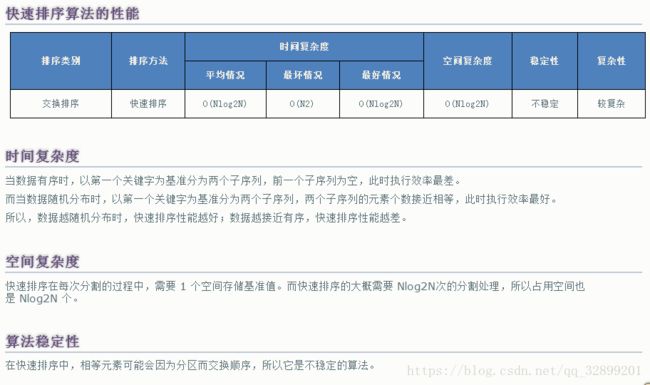
}3.算法时间、空间复杂度、稳定性分析
七、归并排序
1.算法思想:
将待排序序列R[0...n-1]看成是n个长度为1的有序序列,将相邻的有序表成对归并,得到n/2个长度为2的有序表;将这些有序序列再次归并,得到n/4个长度为4的有序序列;如此反复进行下去,最后得到一个长度为n的有序序列。
综上可知:
归并排序其实要做两件事:
(1)“分解”——将序列每次折半划分。
(2)“合并”——将划分后的序列段两两合并后排序。
2.核心代码
(1)如何合并
在每次合并过程中,都是对两个有序的序列段进行合并,然后排序。
这两个有序序列段分别为 R[low, mid] 和 R[mid+1, high]。
先将他们合并到一个局部的暂存数组R2中,带合并完成后再将R2复制回R中。
为了方便描述,我们称 R[low, mid] 第一段,R[mid+1, high] 为第二段。
每次从两个段中取出一个记录进行关键字的比较,将较小者放入R2中。最后将各段中余下的部分直接复制到R2中。
经过这样的过程,R2已经是一个有序的序列,再将其复制回R中,一次合并排序就完成了。
public void Merge(int[] array, int low, int mid, int high) {
int i = low; // i是第一段序列的下标
int j = mid + 1; // j是第二段序列的下标
int k = 0; // k是临时存放合并序列的下标
int[] array2 = new int[high - low + 1]; // array2是临时合并序列
// 扫描第一段和第二段序列,直到有一个扫描结束
while (i <= mid && j <= high) {
// 判断第一段和第二段取出的数哪个更小,将其存入合并序列,并继续向下扫描
if (array[i] <= array[j]) {
array2[k] = array[i];
i++;
k++;
} else {
array2[k] = array[j];
j++;
k++;
}
}
// 若第一段序列还没扫描完,将其全部复制到合并序列
while (i <= mid) {
array2[k] = array[i];
i++;
k++;
}
// 若第二段序列还没扫描完,将其全部复制到合并序列
while (j <= high) {
array2[k] = array[j];
j++;
k++;
}
// 将合并序列复制到原始序列中
for (k = 0, i = low; i <= high; i++, k++) {
array[i] = array2[k];
}
}(2)如何分解
在某趟归并中,设各子表的长度为gap,则归并前R[0...n-1]中共有n/gap个有序的子表:R[0...gap-1], R[gap...2*gap-1], ... , R[(n/gap)*gap ... n-1]。
调用Merge将相邻的子表归并时,必须对表的特殊情况进行特殊处理。
若子表个数为奇数,则最后一个子表无须和其他子表归并(即本趟处理轮空):若子表个数为偶数,则要注意到最后一对子表中后一个子表区间的上限为n-1。
public void MergePass(int[] array, int gap, int length) {
int i = 0;
// 归并gap长度的两个相邻子表
for (i = 0; i + 2 * gap - 1 < length; i = i + 2 * gap) {
Merge(array, i, i + gap - 1, i + 2 * gap - 1);
}
// 余下两个子表,后者长度小于gap
if (i + gap - 1 < length) {
Merge(array, i, i + gap - 1, length - 1);
}
}
public int[] sort(int[] list) {
for (int gap = 1; gap < list.length; gap = 2 * gap) {
MergePass(list, gap, list.length);
System.out.print("gap = " + gap + ":\t");
this.printAll(list);
}
return list;
}3.算法时间、空间复杂度、稳定性分析
八、基数排序
1.算法思想:
不妨通过一个具体的实例来展示一下,基数排序是如何进行的。
设有一个初始序列为: R {50, 123, 543, 187, 49, 30, 0, 2, 11, 100}。
我们知道,任何一个阿拉伯数,它的各个位数上的基数都是以0~9来表示的。
所以我们不妨把0~9视为10个桶。
我们先根据序列的个位数的数字来进行分类,将其分到指定的桶中。例如:R[0] = 50,个位数上是0,将这个数存入编号为0的桶中。
分类后,我们在从各个桶中,将这些数按照从编号0到编号9的顺序依次将所有数取出来。
这时,得到的序列就是个位数上呈递增趋势的序列。
按照个位数排序: {50, 30, 0, 100, 11, 2, 123, 543, 187, 49}。
接下来,可以对十位数、百位数也按照这种方法进行排序,最后就能得到排序完成的序列。