Winograd，GEMM算法综述（CNN中高效卷积实现）（上）

                       高效卷积实现算法和应用综述（上）

在下一篇文章会介绍Winograd算法的应用，在ICLR，CVPR，FPGA，FCCM等机器学习和FPGA领域的定会上的研究实现和新的突破。下一篇理论分析链接。https://blog.csdn.net/qq_32998593/article/details/86181663

摘要：

首先要说明的是，卷积是指ConvNet中默认的卷积，而不是数学意义上的卷积。其实，ConvNet 中的卷积对于与数学中的 cross correlation。

计算卷积的方法有很多种，常见的有以下几种方法：

滑窗：这种方法是最直观最简单的方法。 但是，该方法不容易实现大规模加速，因此，通常情况下不采用这种方法（但是也不是绝对不会用，在一些特定的条件下该方法反而是最高效的）。

im2col：目前几乎所有的主流计算框架包括 Caffe, MXNet 等都实现了该方法. 该方法把整个卷积过程转化成了GEMM过程，而GEMM在各种 BLAS 库中都是被极致优化的，一般来说，速度较快。

FFT：傅里叶变换和快速傅里叶变化是在经典图像处理里面经常使用的计算方法，但是，在 ConvNet中通常不采用，主要是因为在 ConvNet 中的卷积模板通常都比较小，例如 3×3 等，这种情况下，FFT 的时间开销反而更大，所以很少在CNN中利用FFT实现卷积。

Winograd： Winograd 是存在已久最近被重新发现的方法，在大部分场景中, Winograd方法都显示和较大的优势，目前cudnn中计算卷积就使用了该方法。

高效卷积算法之一：

1. BLAS简介

BLAS(Basic Linear Algebra Subprograms)是一组线性代数计算中通用的基本运算操作函数集合[1] 。BLAS库中函数根据运算对象的不同，BLAS库中函数根据运算对象的不同，分为3个level。

Level 1 函数处理单一向量的线性运算以及两个向量的二元运算。Level 1 函数最初出现在1979年公布的BLAS库中。

Level 2 函数处理 矩阵与向量的运算，同时也包含线性方程求解计算。 Level 2 函数公布于1988年。

Level 3 函数包含矩阵与矩阵运算。Level 3 函数发表于1990年。

PGEMM是Level 3中的库，其中函数的语法和描述为：

- Description: matrix matrix multiply

- Syntax: PGEMM( TRANSA, TRANSB, M, N, K, ALPHA, A, LDA, B, LDB, BETA, C, LDC)

- P: S(single float), D(double float), C(complex), Z(complex*16)

详情可以去BLAS的官方文档查询这个卷积实现算法。

向量和矩阵运算是数值计算的基础，BLAS库通常是一个软件计算效率的决定性因素。除了BLAS参考库以外，还有多种衍生版本和优化版本。这些BLAS库实现中，有些仅实现了其它编程语言的BLAS库接口，有些是基于BLAS参考库的Fortran语言代码翻译成其它编程语言，有些是通过二进制文件代码转化方法将BLAS参考库转换成其它变成语言代码，有些是在BLAS参考库的基础上，针对不同硬件(如CPU，GPU)架构特点做进一步优化。

几个比较著名的基于BLAS库开发的高级库包括：

Intel® Math Kernel Library

Intel® Math Kernel Library (Intel® MKL) accelerates math processing and neural network routines that increase application performance and reduce development time. Intel MKL includes highly vectorized and threaded Linear Algebra, Fast Fourier Transforms (FFT), Neural Network, Vector Math and Statistics functions. The easiest way to take advantage of all of that processing power is to use a carefully optimized math library. Even the best compiler can’t compete with the level of performance possible from a hand-optimized library. If your application already relies on the BLAS or LAPACK functionality, simply re-link with Intel MKL to get better performance on Intel and compatible architectures.

cuBLAS

The NVIDIA CUDA Basic Linear Algebra Subroutines (cuBLAS) library is a GPU-accelerated version of the complete standard BLAS library that delivers 6x to 17x faster performance than the latest MKL BLAS.

clBLAS

This repository houses the code for the OpenCL™ BLAS portion of clMath. The complete set of BLAS level 1, 2 & 3 routines is implemented.

2. GEMM分析

GEMM在深度学习中是十分重要的，全连接层以及卷积层基本上都是通过GEMM来实现的，而网络中大约90%的运算都是在这两层中。而一个良好的GEMM的实现可以充分利用系统的多级存储结构和程序执行的局部性来充分加速运算。

Matrix-Matrix multiplication中，BLAS的两个矩阵相乘的标准接口是：

dgemm( transa, transb, m, n, k, alpha, A, lda, B, ldb, beta, C, ldc)

这个接口的主要功能为计算：

而transa和transb可以分别指定矩阵A和矩阵B是否进行转置；A的计算维度为m×k，矩阵B的计算维度为k×n，矩阵C的计算维度为m×n；ldX表示矩阵X的行数（这个的参数，可能有的同学会说，不是跟m或者n或者k一样吗？其实不然，这个参数的功能是让这个接口能够使得A本身比计算维度大，只使用子矩阵来进行计算，m≤lda）。接下来开始对这个接口进行优化。

GEMM算法基础：

则根据矩阵相乘的定义，可得C=AB+C的计算公式为：

从而可将其实现为：

for i=0:m-1
    for j=0:n-1
        for p=0:k-1
            C(i,j):=A(i,p)*B(p,j)+C(i,j)
        endfor
    endfor
endfor

 可以看出，根据定义实现的算法计算复杂度为O(mnk)，也就是O(n^3)。

常规的卷积操作为：

3维卷积运算执行完毕，得一个2维的平面：

将卷积操作的3维立体变为二维矩阵乘法，可以调用BLAS中的GEMM库，按 [kernel_height, kernel_width, kernel_depth] ⇒ 将输入分成 3 维的 patch，并将其展成一维向量：

此时的卷积操作就可转化为矩阵乘法：

由于内存中二维数组是以行优先进行存储的，因此B[k][j]存在严重的cache命中率问题，解决这个问题的方法是也将B进行一次沿对角线进行翻转，使得最里面的计算变成row直接取出来。

从下图可以看出，一个CNN模型运算过程中，基本上的时间都来消耗在CONV操作上。（图像来自于贾扬清毕业论文，论文地址）

高效卷积算法之二：

Winograd算法简介

这个算法用更多的加法来代替乘法，在FPGA上，由于乘法的计算消耗更多的资源和时钟，往往是很慢的。一般的乘法需要借助FPGA中的DSP来计算，DSP的大小有18 bits X 25 bits的乘法，如果两个浮点数较大，则需要更多的乘法。采用Winograd卷积算法，借助LUT来计算乘法，会节省FPGA的资源，加快速度。

因此，我们可以在filter 维度较小情况下应用winograd 做卷积。

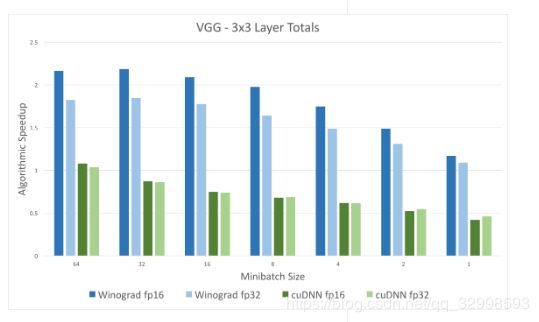
以下是一些实际运算中，采用该方法的性能对比结果：

从上面的对比可以看出，利用Winograd算法进行卷积，比NVIDIA的深度学习库cuDNN中的卷积计算快很多。其中cuDNN的卷积是GEMM算法实现。batch_size越大，加速效果越明显，因为越大的batch_size，计算的负载并不是线性的增加，开辟的内存地址和GPU的显存被充分计算应用，增加的一部分空间，平均到一个样本数上，计算时间更短，速度更明显。这个理论在Google的一篇论文上也具体介绍了batch_size的影响。（图片来自于Intel官方提供的对比，对比图像地址 ）

反过来看精度，Winograd算法的实现和直接卷积（原始的卷积实现）的效果差不多4X4，2X2的Winograd卷积核效果都不怎么掉。说明Winograd算法是一种高效的卷积算法。有值得发掘的价值。

在下一篇文章会介绍Winograd算法的应用，在ICLR，CVPR，FPGA，FCCM等机器学习和FPGA领域的定会上的研究实现和新的突破。请点击下一篇综述。https://blog.csdn.net/qq_32998593/article/details/86181663