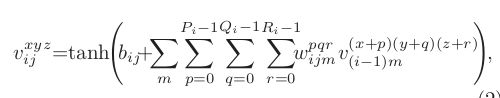深度学习之3D卷积神经网络

一、概述

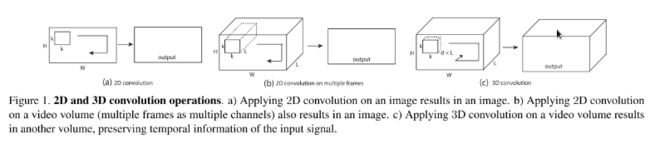
3D CNN主要运用在视频分类、动作识别等领域，它是在2D CNN的基础上改变而来。由于2D CNN不能很好的捕获时序上的信息，因此我们采用3D CNN，这样就能将视频中时序信息进行很好的利用。首先我们介绍一下2D CNN与3D CNN的区别。如图1所示，a)和b)分别为2D卷积用于单通道图像和多通道图像的情况（此处多通道图像可以指同一张图片的3个颜色通道，也指多张堆叠在一起的图片，即一小段视频），对于一个滤波器，输出为一张二维的特征图，多通道的信息被完全压缩了。而c)中的3D卷积的输出仍然为3D的特征图。也就是说采用2D CNN对视频进行操作的方式，一般都是对视频的每一帧图像分别利用CNN来进行识别，这种方式的识别没有考虑到时间维度的帧间运动信息，而使用3D CNN能更好的捕获视频中的时间和空间的特征信息。

                                                                                         图一 

 二、原理

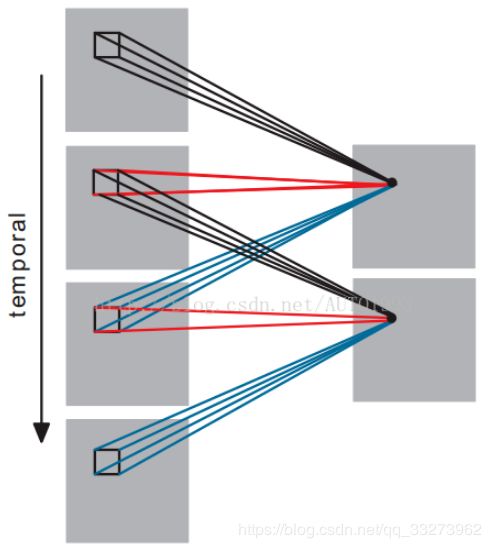
首先我们看一下3D CNN是如何对时间维度进行操作的，如图二所示，我们将时间维度看成是第三维，这里是对连续的四帧图像进行卷积操作，3D卷积是通过堆叠多个连续的帧组成一个立方体，然后在立方体中运用3D卷积核。在这个结构中，卷积层中每一个特征map都会与上一层中多个邻近的连续帧相连，因此捕捉运动信息。

                                                                                                   图二 

注：3D卷积核只能从cube中提取一种类型的特征，因为在整个cube中卷积核的权值都是一样的，也就是共享权值，都是同一个卷积核（图中同一个颜色的连接线表示相同的权值）。我们可以采用多种卷积核，以提取多种特征 。

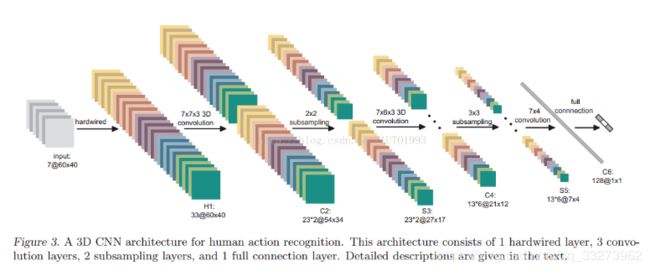
图三是3D卷积神经网络的整体架构

                                                                                                    图三 

input—>H1

      神经网络的输入为7张大小为60*40的连续帧，7张帧通过事先设定硬核（hardwired kernels）获得5种不同特征：灰度、x方向梯度、y方向梯度、x方向光流、y方向光流，前面三个通道的信息可以直接对每帧分别操作获取，后面的光流（x，y）则需要利用两帧的信息才能提取，因此H1层的特征maps数量：（7+7+7+6+6=33），特征maps的大小依然是60* 40。

H1—>C2

     用两个7*7*3的3D卷积核对5个channels分别进行卷积，获得两个系列，每个系列5个channels（7*  7表示空间维度，3表示时间维度，也就是每次操作3帧图像），同时，为了增加特征maps的个数，在这一层采用了两种不同的3D卷积核，因此C2层的特征maps数量为：（（（7-3）+1）*  3+（（6-3）+1）*  2）*  2=23*  2。这里右乘的2表示两种卷积核。特征maps的大小为：（（60-7）+1）*  （（40-7）+1）=54 * 34。然后为卷积结果加上偏置套一个tanh函数进行输出。（典型神经网。）

  C2—>S3

   2x2池化，下采样。下采样之后的特征maps数量保持不变，因此S3层的特征maps数量为：23 *2。特征maps的大小为：（（54 / 2） *  （34 /2）=27  *17

S3—>C4

   为了提取更多的图像特征，用三个7*6*3的3D卷积核分别对各个系列各个channels进行卷积，获得6个系列，每个系列依旧5个channels的大量maps。

我们知道，从输入的7帧图像获得了5个通道的信息，因此结合总图S3的上面一组特征maps的数量为（（7-3）+1） * 3+（（6-3）+1） * 2=23,可以获得各个通道在S3层的数量分布：

前面的乘3表示gray通道maps数量= gradient-x通道maps数量= gradient-y通道maps数量=（7-3）+1）=5；

后面的乘2表示optflow-x通道maps数量=optflow-y通道maps数量=（6-3）+1=4；

假设对总图S3的上面一组特征maps采用一种7 6 3的3D卷积核进行卷积就可以获得：

（（5-3）+1）* 3+（（4-3）+1）* 2=9+4=13；

三种不同的3D卷积核就可获得13* 3个特征maps，同理对总图S3的下面一组特征maps采用三种不同的卷积核进行卷积操作也可以获得13*3个特征maps，

因此C4层的特征maps数量：13* 3* 2=13* 6

C4层的特征maps的大小为：（（27-7）+1）* （（17-6）+1）=21*12

然后加偏置套tanh。

C4—>S5

3X3池化，下采样。此时每个maps的大小：7* 4。通道maps数量分布情况如下：

gray通道maps数量= gradient-x通道maps数量= gradient-y通道maps数量=3

optflow-x通道maps数量=optflow-y通道maps数量=2；

S5—>C6

      进行了两次3D卷积之后，时间上的维数已经被压缩得无法再次进行3D卷积（两个光流channels只有两个maps）。此时对各个maps用7*42D卷积核进行卷积，加偏置套tanh（烦死了！），获得C6层。C6层维度已经相当小，flatten为一列有128个节点的神经网络层。

C6—>output

      经典神经网络模型两层之间全链接，output的节点数目随标签而定。

三、应用

这里可以将3D卷积神经网络应用在卷积自编码器上，最近看了一篇3D CAE在高光谱图像上应用的文章：LEARNING SENSOR-SPECIFIC FEATURES FOR HYPERSPECTRAL IMAGES VIA 3-DIMENSIONAL CONVOLUTIONAL AUTOENCODER。这篇文章将高光谱图像的波段这一维转化成3D卷积神经网络的时间维，在卷积自编码器中使用3D卷积，得到了很好的效果，下面是其中卷积核和通道的变化表格。

 

参考：

https://blog.csdn.net/qq_25737169/article/details/75072014 

https://blog.csdn.net/AUTO1993/article/details/70948249

https://www.cnblogs.com/Ponys/p/3450177.html