[100天每天一个算法--第1天] 背包算法
其实PHP程序员需不需要学算法,要不要深挖算法,一直没个定论。博主本人准大四,在找实习的过程中逐渐发现学习算法的重要性,博主以前在学校的工作室老大说过一句话,熟悉算法,可以让你的天花板更高一些,所以便有了这个博客系列,每天一个算法来由简到难逐步提升自己的编程能力。
今天博主想讲一下背包算法.。
由一道题开始,情景如下:
0-1背包问题:
n个物品和1个背包,每个物品i对应的重量为wi,价值为vi,背包的容量为W。每个物品只有一件,要么装入,要么不装入,不可拆分。如何选取物品装入背包,使背包所装入的物品的总价值最大?要求算法输出最优值和最优解。
1)问题分析
在选择装入背包的物品时,对于物品i只有两种选择,即装入背包或不装入背包。不能将物品i装入背包多次,也不能只装入物品i的一部分。假设xi表示物品i被装入背包的情况,当xi=0时,表示物品没有被装入背包;当xi=1时,表示物品被装入背包。
2)算法思想及算法设计
算法思想:
根据问题分析,设计出如下的约束条件和目标函数
![[100天每天一个算法--第1天] 背包算法_第1张图片](http://img.e-com-net.com/image/info8/41b94f34c79248c08674bf71b37c96d0.jpg)
![[100天每天一个算法--第1天] 背包算法_第2张图片](http://img.e-com-net.com/image/info8/81ae074f6ae0489ca82f8af77637c404.jpg)
于是,问题归结为寻找一个满足约束条件,并使目标函数达到最大的解向量X=(x1,x2,x3,…xn)。
由于0-1背包问题的解是用向量(x1,x2,x3,…xn)来描述的。该问题可以看做是决策一个n元0-1向量(x1,x2,x3,…xn)。对于任意一个分量xi的决策是“决定xi=1或xi=0”,i=1,2,3…,n。对于xi-1决策后,序列(x1,x2,x3,…xn)已被确定,在决策xi时,问题处于下列两种状态之一:
(1)背包容量不足以装入物品i,则xi=0,装入背包的价值不增加
(2)背包容量足以装入物品i,则xi=1,装入背包的价值增加vi
在这两种情况下,装入背包的价值最大者应该是对xi决策后的价值
令C[i][j]表示子问题![[100天每天一个算法--第1天] 背包算法_第3张图片](http://img.e-com-net.com/image/info8/6b903c600b2a44a298663b04d3667e10.jpg) 的最优值,即
的最优值,即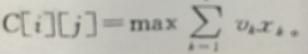 。那么,C[i-1][j-wixi]表示该问题的子问题
。那么,C[i-1][j-wixi]表示该问题的子问题![[100天每天一个算法--第1天] 背包算法_第4张图片](http://img.e-com-net.com/image/info8/0dc2521910974d68bea9e7a3d7e8c3aa.jpg) 的最优值。
的最优值。
经分析可得最优值的递归定义式为:
![[100天每天一个算法--第1天] 背包算法_第5张图片](http://img.e-com-net.com/image/info8/17d71dc8a5f14b6681e4e861150dad05.jpg)
算法设计:
1:采用数组w[n]来存放n个物品的重量;数组v[n]来存放n个物品的价值,背包容量为W,数组C[n+1][w+1]来存放每一次迭代的执行结果;数组x[n]用来存储所装入背包的物品状态。
2:初始化。按上面递归式初始化数组C
3:循环阶段。按上面递归式确定前i个物品能装入背包的情况下得到的最优值
3-1:i=1时,求出C[1][j],1≤j≦W.
3-2: i=2时,求出C[2][j],1≤j≤W
以此类推,直到。。。。
3-n: i=n时,求出C[n][W],1≤j≤W。此时,C[n][W]便是最优值。
4:确定装入背包的具体物品。从C[n][W]的值往前推,如果C[n][W]>C[n-1][W],则xn=1,前n-1个物品被装入容量W-wn的背包中,否则xn=0。以此类推。。。。
得到以下关系式:
xi=0, j=j 当C[i][j] = C[i-1][j]
Xi=1, j =j-wi 当C[i][j]>C[i-1][j]
按照式子,即可确定装入背包的具体物品
3)图解
物品重量:w1 =7 w2 =23 w3=25 w4 =24
物品价值:v1 =1 v2 =8 v3 =19 v4 =11
根据算法设计步骤,图解如下
采用二维数组C[5][53]来存放各个子问题的最优值,行i表示物品,列j表示背包容量,表中数据表示C[i][j]
(1)根据公式初始化第0行和第0列,如下图所示

(2)i=1时,求出C[1][j],1≤j≤W。
由于物品1的重量w1=7,价值等于v1=1,分两种情况讨论
1.如果j < wi,即j<7时,C[1][j] = C[0][j]
2.如果j ≥ w1,即j≥7时,C[1][j]=max{C[0][j],C[0][j-w1]+v1}=max{C[0][j]},C[0][j-7]+1}
i=1时的内容如下图

(3)i=2时,求出C[2][j],1≤j≤W。
由于物品2的重量w2=23,价值等于v2=8,分两种情况讨论
1.如果j < w2,即j<23时,C[2][j] = C[1][j]
2.如果j ≥ w2,即j≥23时,C[2][j]=max{C[1][j],C[1][j-w2]+v2}=max{C[1][j]},C[1][j-23]+8}
i=2时的内容如下图

(4)i=3时,求出C[3][j],1≤j≤W。
由于物品3的重量w3=25,价值等于v3=19,分两种情况讨论
1.如果j < w3,即j<25时,C[3][j] = C[2][j]
2.如果j ≥ w3,即j≥25时,C[3][j]=max{C[2][j],C[2][j-w3]+v3}=max{C[2][j]},C[2][j-25]+19}
i=3时的内容如下图

(5)i=4时,求出C[4][j],1≤j≤W。
由于物品4的重量w4=24,价值等于v4=11,分两种情况讨论
1.如果j < w4,即j<24时,C[4][j] = C[3][j]
2.如果j ≥ w4,即j≥24时,C[4][j]=max{C[3][j],C[3][j-w4]+v4}=max{C[4][j]},C[4][j-24]+11}
i=4时的内容如下图

最终,从图5可以看出,装入背包的物品的最大价值是30
(6)从C[n][W]的值往前推,最终可求出装入背包的具体物品,即问题的最优解,
初始时,j=W=52,i=4。
C[4][52]>C[3][52],第4个物品被装入背包,x4=1,j=j-24=28.
C[3][28]>C[2][28],第3个物品被装入背包,x3=1,j=j-25=3.
C[2][3]=C[1][3],第2个物品没有被装入背包,x2=0.
C[1][3]=C[0][3],第1个物品没有被装入背包,x1=0.
求得问题最优解为X=(x1,x2,x3,x4)=(0,0,1,1);
4)算法描述
/*
*背包算法类
*/
class bag {
private $n;//物品的数量
private $W;//背包总容量
private $w = array();//物品的重量数组
private $v = array();//物品的价值
public function __construct ($n,$W,$w,$v) {
//构造函数初始化基本数据
$this->n = $n;
$this->W = $W;
$this->w = $w;
$this->v = $v;
}
//背包算法
public function knapsack () {
$n = $this->n;
$w = $this->w;
$v = $this->v;
$W = $this->W;
$C[$n][$n] = [];
$x[$n] = [];
for ($i=0; $i<=$n; $i++) {
$C[$i][0] = 0; //初始化第0列
}
for ($i = 0; $i <= $W; $i++) {
$C[0][$i] = 0; //初始话第0行
}
for ($i = 1;$i <= $n;$i++) { //计算C[$i][$j]
for ($j=1; $j <= $W; $j++) {
if ($j < $w[$i-1]) {
$C[$i][$j] = $C[$i-1][$j];
} else {
$C[$i][$j] = max($C[$i-1][$j],$C[$i-1][$j-$w[$i-1]] + $v[$i-1]);
}
}
}
//构造最优解
$j = $W;
for ($i = $n;$i > 0; $i--) {
if ($C[$i][$j] > $C[$i-1][$j]) {
$x[$i] = 1;
$j -= $w[$i-1];
} else {
$x[$i] = 0;
}
}
ksort($x);
return $data = ['maxvalue' => $C[$n][$W], 'maxroad' => $x];//maxvalue为最大价值,maxroad为最优解
}
}5)算法分析验证
a.算法复杂度分析(时间复杂度、空间复杂度)
时间复杂度:在knapsack中,第三个循环是两层嵌套的for循环,为此,可选定语句 if ( j< j < w[$i-1] ) 作为基本语句,其运行时间为n × W,由此可见,时间复杂度为O(n×W)。
空间复杂度:与时间复杂度一样均为O(n×W)
b.算法正确性验证
浏览器输入代码地址 没有报错
6)算法实现和测试
a. 运行环境
php-5.6.27 Apache 2.4.23 windows系统
b. 输入数据
$weight = [7,23,25,24];//输入物品重量数组
$value = [1,8,19,11];//输入物品价值
$bag = new bag(4,52,$weight,$value); //实例化背包类
$data = $bag->knapsack();//调用背包算法
var_dump($data);//打印结果
c. 输出结果
array(2) {
["maxvalue"] => int(30)
["maxroad"] =>
array(4) {
[1] => int(0)
[2] => int(0)
[3] => int(1)
[4] => int(1)
}
}