Leetcode学习之栈、队列、堆（3）

开宗明义：本系列基于小象学院林沐老师课程《面试算法 LeetCode 刷题班》，刷题小白，旨在理解和交流，重在记录，望各位大牛指点！

---

Leetcode学习之栈、队列、堆（3）

---

---

1、STL优先级队列（二叉堆）

堆：通常可以被看做一棵树，它满足下列性质：

1. 堆中任意节点的值总是不大于(不小于)其子节点的值；
2. 堆总是一棵完全树。

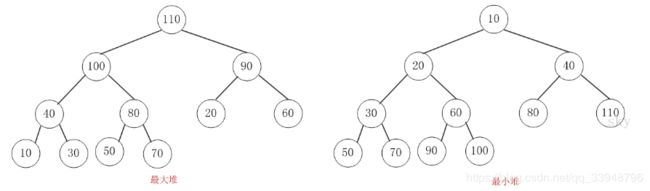
二叉堆：二叉堆是完全二元树或者是近似完全二元树，它分为两种：最大堆和最小堆。
最大堆：父结点的键值总是大于或等于任何一个子节点的键值；
最小堆：父结点的键值总是小于或等于任何一个子节点的键值。

二叉堆，也叫优先级队列，STL包含到 $\#include<queue>$中。
测试代码：

#include 
#include 
using namespace std;

//优先输出大数据
//priority_queue
//Type为数据类型， Container为保存数据的容器，Functional为元素比较方式。
//如果不写后两个参数，那么容器默认用的是vector，比较方式默认用operator<，也就是优先队列是大顶堆，队头元素最大。

int main() {
	priority_queue<int> big_heap;//默认构造的就为最大堆、

	//priority_queue, isgreater> small_heap;//最小堆构造方法
	priority_queue<int, std::vector<int>, std::less<int>> big_heap2;//最大堆构造方法

	if (big_heap.empty()) {
		printf("big_heap is empty!\n");
	}

	int test[] = { 6,10,1,7,99,4,33 };
	for (int i = 0; i < 7; i++) {
		big_heap.push(test[i]);//把元素push进入最大堆
	}
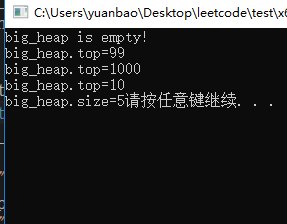
	printf("big_heap.top=%d\n", big_heap.top());//打印这个优先级队列的第一个元素，普通的queue是33,但是最大堆应为99
	big_heap.push(1000);
	printf("big_heap.top=%d\n", big_heap.top());//这时候应该1000
	for (int i = 0; i < 3; i++) {
		big_heap.pop();
	}
	printf("big_heap.top=%d\n", big_heap.top());//这时候应该10
	printf("big_heap.size=%d", big_heap.size());
	system("pause");
	return 0;
}

效果图：

---

2、求数组中第K大的数(Top K) Leetcode 215.

题目来源：$Leetcode215.KthLargestElementinanArray$
题目描述：已知一个未排序的数组，求这个数组中第K大的数字，如，array=[3,2,1,5,6,4],k=2,return 5。
思路：维护一个K大小的最小堆，堆中元素个数小于K时，新元素直接进入堆中；否则，当堆顶的元素小于新元素时，弹出堆顶，将新元素加入堆，注意啊：加入堆的话，会调整堆，因为这个堆只有k大小，进来一个就会出去一个。这样做的理由：使用的堆为最小堆，堆顶是堆中最小的元素，新元素都会保证比堆顶小，因为新元素比堆顶大的话，会进入堆，调整堆。所以堆中K个元素是已扫描的元素里最大的K个。堆顶即第K大的数。
设数组长度为$N$，求第$K$大的数，时间复杂度为：$N\ast logK$。

测试代码：

#include 
#include 
using namespace std;

class Solution {
public:
	//这边是重载
	template <class _Tp>
	struct greater : public binary_function<_Tp, _Tp, bool>
	{
		bool operator()(const _Tp& __x, const _Tp& __y) const { return __x > __y; }
	};

	int findKthLargest(vector<int>& number, int k) {
		priority_queue<int, vector<int>, greater<int>> Q;
		for (int i = 0; i < number.size(); i++) {//遍历number数组
			if (Q.size()<k) {//如果堆中元素个数小于K，直接push进入堆
				Q.push(number[i]);
			}
			else if (number[i] > Q.top()) {//如果堆顶比新元素小，弹出堆顶
				Q.pop();
				Q.push(number[i]);//push进入，代替新元素
			}
		}
		return Q.top();//返回堆顶
	}
};

int main() {
	vector<int> nums;
	nums.push_back(3);
	nums.push_back(2);
	nums.push_back(1);
	nums.push_back(5);
	nums.push_back(6);
	nums.push_back(4);
	Solution solve;
	printf("%d\n", solve.findKthLargest(nums, 2));
	system("pause");
	return 0;
}

效果图：

---

3、寻找中位数 Leetcode 295.

题目来源：$Leetcode295.FindMedianfromDataStream$
题目描述：设计一个数据结构，该数据结构动态维护一组数据，且支持如下操作：
1、添加元素：void addNum(int num)，将整型num添加至数据结构中。
2、返回数据的中位数：double findMedian()，返回其维护的数据的中位数。
其中，中位数的定义：
1.若数据个数为奇数，中位数是该组数排序后中间的数。如[1,2,3]->2。
2. 若数据个数为偶数，中位数是该组数排序后中间两个数字的平均值。如[1,2,3,4]->2.5。
要求描述：

思路：
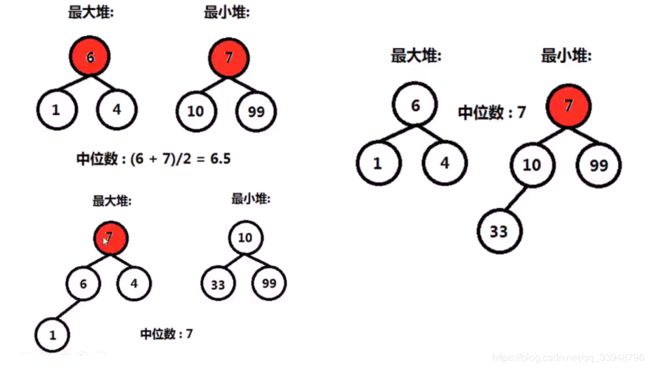
复杂度太高->巧用堆的性质：动态维护一个最大堆与最小堆，最大堆存储一半数据，最小堆存储一半的数据，维持的状态是：最大堆的堆顶比最小堆的堆顶小。
有三种情形：①偶数，最大堆与最小堆各一半；
②奇数，最大堆比最小堆多一个元素；
③奇数，最大堆比最小堆少一个元素；

测试代码：

#include 
#include 

using namespace std;

class Solution {
public:
	//这边是重载
	template <class _Tp>
	struct greater : public binary_function<_Tp, _Tp, bool>
	{
		bool operator()(const _Tp& __x, const _Tp& __y) const { return __x > __y; }
	};

	priority_queue<int, std::vector<int>, greater<int>> small_queue;//最小堆构造方法
	priority_queue<int, std::vector<int>, std::less<int>> big_queue;//最大堆构造方法

	void addNum(int num) {
		if (big_queue.empty()) {  
			big_queue.push(num);
			return;
		}
		if (big_queue.size() == small_queue.size()) {
			if (num < big_queue.top()) {
				big_queue.push(num);
			}
			else
			{
				small_queue.push(num);
			}
		}
		else if(big_queue.size() > small_queue.size())
		{
			if (num >big_queue.top()) {
				small_queue.push(num);
			}
			else
			{
				small_queue.push(big_queue.top());
				big_queue.pop();
				big_queue.push(num);
			}
		}
		else if (big_queue.size() < small_queue.size()) {
			if (num < small_queue.top()) {
				big_queue.push(num);
			}
			else
			{
				big_queue.push(small_queue.top());
				small_queue.pop();
				small_queue.push(num);
			}
		}
	}

	double findMedian() {
		if (big_queue.size() == small_queue.size()) {
			return (big_queue.top() + small_queue.top()) / 2;
		}
		else if (big_queue.size() > small_queue.size()) {
			return big_queue.top();
		}
		return small_queue.top();
	}
};

int main() {
	Solution solve;
	int test[] = { 6,10,1,7,99,4,33 };
	for (int i = 0; i < 7; i++) {
		solve.addNum(test[i]);
		printf("%1f\n", solve.findMedian());
	}
	system("pause");
	return 0;
}

效果图：