散列表的构造和哈希冲突
----------------------------该篇文章主要写了散列表的6中构造方法以及处理哈希冲突的两种方法----------------------------
一、散列表的构造
1.直接定址法:
直接定址法是根据关键字得到的某一线性函数值作为散列表地址。f(key) = a*key+b,(其中a,b都为常数)
这种方法比较简单,但也有缺陷,这种定址方法需要事先知道关键字的分布情况,且查找时比较适合在表小且连续的表中查找。
2.除留余数法:
除留余数法是经常用来构造散列表的一种方法。看名字很容易想到这种定址方法就是:用关键字除某一个数p得到的余数作为散列表的地址,f(key) = key % p,(这里的p就为表的大小)。
但是这里又引来问题了,很可能有好几个关键字都映射在一个地址上,比如:当表长p为5,关键字key有1,15,26,30等时,1和26就都映射在散列地址为1的位置上,这种情况就是哈西冲突(底下有讲^-^)。
所以,这里选取表的大小p就显得尤为重要。一般来讲,p都尽量取素数值,这样能降低哈希冲突的概率,注意,哈希冲突是不能被避免的,任意的散列表都有可能存在哈希冲突!!!
3.数字分析法:
假如我们现在需要对某一公司员工进行登记,用他们的电话当作关键字来存储,由于电话号码中只有后四位才是真正的用户,那么很可能前7位数字都是一样的。
130 **** 1212
130 **** 2291
137 **** 0912
137 **** 9238
137 **** 1832
所以,我们就用后四位当作散列地址进行存储。当然,这样也会出现冲突,我们就可以对抽取的数字进行左环移位、右环移位、反转后者将前两位与后两位叠加的方法(如:1832----18+32=50)
如果事先知道关键字分布且关键字的若干位分布均匀时,就可以选用此方法。
4.折叠法:
首先,我们将关键字均匀分割成位数相等的几组(最后一组假如位数不够也可以短一些),然后将这几组数进行相加,得到和以后,根据表的大小取后几位作为散列地址。
例如:现已知表长为3,有关键字:9876543210,我们将其分割称987,654,321,0四组,987+654+321+0=1962,我们就取962为散列地址。
这种方法事先不需要知道关键字的分布情况,且关键字位数较大时适合用折叠法。
5.平方取中法:
如现在有关键字1234,我们将1234取平方后得到1522756,我们就取中间的三位227作为其散列地址。如果关键字时4321, 4321^2=18671041,我们就可以取671或者710作为其散列地址。
用这种方法时事先不需要知道关键字的分布情况,且当关键字位数又不是很大!
6.随机数法:
随机数法需要用到随机数函数random,即 f(key) = random(key)
当关键字的长度不等时可以采用这种方法构造散列表。。
二、哈希冲突
1.哈希冲突---当不同的key值经过相同的哈希函数处理以后可能产生相同的哈希地址(也是上边讲的散列地址),我们称这种情况为哈希冲突/哈希碰撞。
2.哈希冲突的处理
(1)开放定址法-----闭散列方法
当发生哈希冲突后,就去寻找下一个空的散列地址,只要散列表足够大,这个空的位置一定能找到。
开放定址法处理哈希冲突的方法有两种:线性探测和二次探测
【线性探测】
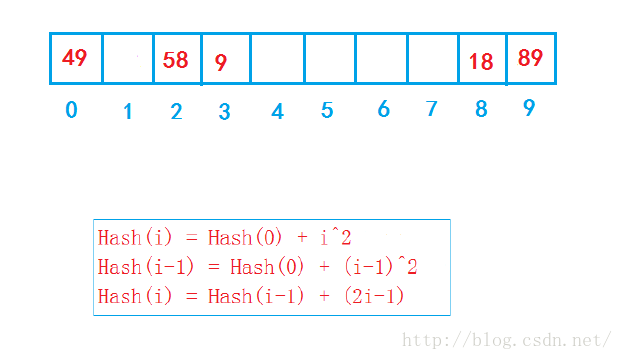
现将89,18,49,58,9插入到散列表中,假设表长度为10,当要插入49时,此时9这个位置已经存在89,那么就继续对下一个位置进行探测,当到表尾时还没有空位置,此时就返回表头继续找寻空位置。
Hash(key)+0, Hash(key)+1, Hash(key)+2 …… Hash(key)+i
这是这5个数插入表中的图:
【二次探测】
如果在上表中继续插入2,可是当插入2时,2的位置上已经有9,此时又会有冲突,我们又需要处理冲突,当数据个数多了以后,无论是插入还是查找效率都会降低。因此我们可以改进:
Hash(key)+0^2, Hash(key)+1^2, Hash(key)+2^2 …… Hash(key)+i^2,即每次查找的是距离上一个为i^2个距离的位置。
下图是89,18,49,58,9插入后的散列表
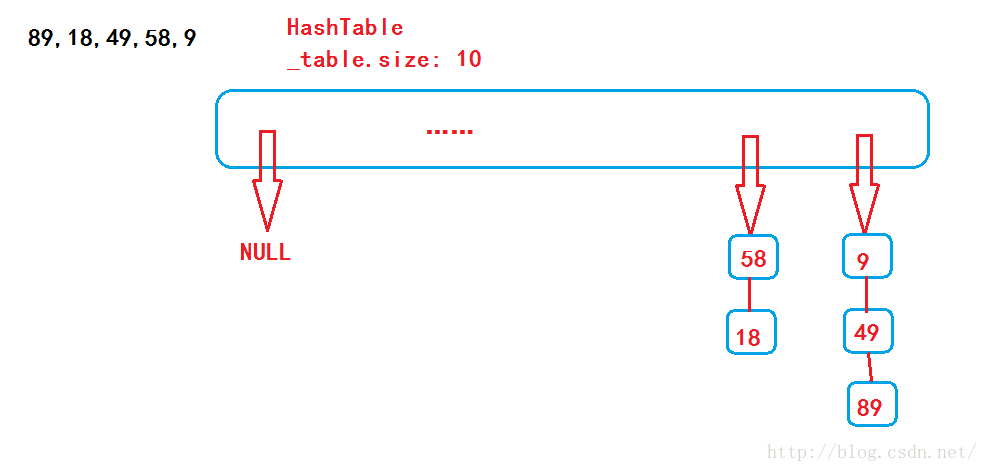
(2)开链法/拉链法(哈希桶)
当发生冲突时,该位置上的数据会用链表链起来,当表中的某些位置没有结点时,该位置就为NULL!!这种方法在实现时就需要多加一个next指针,使这些结点才能链起来。