深度学习总结三：特征处理流程

推荐1

步骤1：数据审查

观察数据集中趋势、离中趋势、分布形状、缺失、重复值、异常值、共线性（相关性）
判断共线性（相关性）的方法：
1.皮尔逊相关系数（连续性变量）:$$r_{pb}=\frac{{\sum }_{i=0}(x_i-x_{avr})(y_i-y_{avr})}{\sqrt{{\sum }_{i=0}(x_i-x_{avr}{)}^2(y_i-y_{avr}{)}^2}}$$

from scipy.stats import pearsonr
pearsonr([1,2,3,5,8], [0.11,0.12,0.13,0.15,0.18])
out(2):(1.0, 0.0)

$r_{pb}$=1，p=0 。
p值是该序列产生于一个不相关系统的概率，p值越高，我们越不能信任这个相关系数。上面测试显示这两个是正相关。
2.卡方检验（离散型变量）：
说明
3.互信息法:计算各个特征的信息增益
4.画多个散点图
判断异常值的方法(异常值是针对单变量说的)：

1. 业务理解
   打个比方，比如一个人数据里面，显示一个人的年龄是200岁，这显然不合常理，需要当作异常值。
2. 3倍标准差准则
   平均值的三倍标准差之外的值。

	ageMean = np.mean(data_train['age'])
	ageStd = np.std(data_train['age'])
	#round()方法返回浮点数x的四舍五入值
	ageUpLimit = round((ageMean + 3*ageStd), 2)
	ageDownLimit = round((ageMean - 3*ageStd), 2)

3. 箱型图检验
   令IQR = 上四分位数减去下四分位数,接着，如果一个数据的值-上4分位数 > 3 *IQR,就认为是一个极端异常的值; 如果一个数据的值-上4分位数 > 1.5 *IQR但是小于3倍的IQR，就认为是温和异常值。
   当然在实践过程中，并非真的要把图画出来，可以只要根据公式保留就好了。

	agePercentile = np.percentile(data_train['age'], [0,25,50,75,100])
	ageIQR = agePercentile[3] - agePercentile[1]
	ageUpLimit = agePercentile[3] + ageIQR * 1.5
	ageDownLimit = agePercentile[3] - ageIQR * 1.5

箱型图说明

	import matplotlib.pyplot as plt
	import numpy as np
	
	np.random.seed(1)
	all_data = [np.random.normal(0, std, size = 100)for std in range(1,4)]
	labels = ['x1', 'x2', 'x3']
	fig, axes = plt.subplots(nrows = 1, ncols = 2, figsize = (16,9))
	
	bplot1 = axes[0].boxplot(all_data, notch=True,vert=True,patch_artist=True, labels = labels)
	axes[0].set_title('Rectangular box plot')
	
	bplot2 = axes[1].boxplot(all_data, notch=True,vert=True,patch_artist=True, labels = labels)
	axes[1].set_title('Notched box plot')
	
	colors = ['pink', 'lightblue', 'lightgreen']
	for bplot in (bplot1, bplot2):
	    for patch, color in zip(bplot['boxes'], colors):
	        patch.set_facecolor(color)
	        
	for ax in axes:
	    ax.yaxis.grid(True)
	    ax.set_xlabel('Three separate sample')
	    ax.set_ylabel('Observed values')
	    
	plt.show()

步骤2：数据清洗

缺失值处理
1.使用均值、中位数、总数插补。用变量的集中趋势来代替。相当于”不求有功，但求无过“。
2.用最近邻插补，根据上一行和下一行的数据求平均作为这一行的值。
3.回归的方法。先用没有缺失的数据建立一个回归模型，再用这个回归模型来预测这个缺失值的值。
4.使用固定值。根据业务理解填充。例子：比如我有一份广州市的工资表，其中有一个缺失值，这时候我可以用广州市的月基本工资标准来填充。
5.插值法：拉格朗日插值法、牛顿插值法、Hermite插值法、分段插值法、样条插值法。
例如：

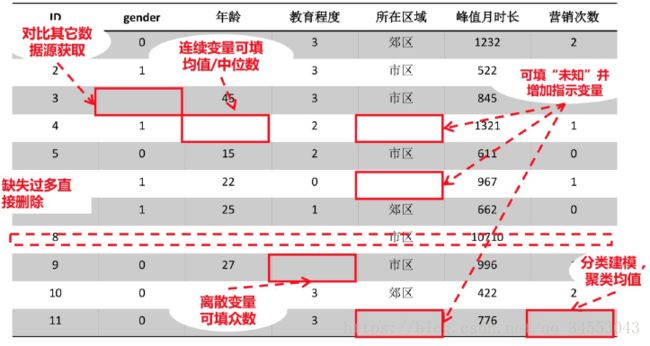
噪声值处理
没用的特征留保存在数据集中会变成噪声，导致模型过拟合。噪声处理可当做共线性处理。
不一致数据处理
异常值处理
1.数据量多的时候，删掉几个不影响的情况下可以选择删掉；
2.可以使用平滑的方法进行补全；
3.可以把异常值作为一种情况处理（不是很确定）
4.或者作为缺失值处理
重复值处理
共线性处理
共线性说明
主成分分析或者因子分析。不是直接删除共线的特征——一般两个特征有共线性，是把两个特征合成一个。直接丢掉可能会损失信息，所以一般是融合。例如：要衡量一个城市的经济实力，选取了这个城市的GDP和人均GDP，那么这两个变量根据经验是会存在共线性的，它们在某种程度上都代表了这个城市的经济水平，这时候通常就会融合成“经济水平”这个变量。最终的经济水平是由城市GDP指标和人均GDP指标线性组合而成的，比如经济水平 = 0.2 * Norm(GDP) + 0.8 * Norm(RGDP) 。要归一化消除量纲的影响。
融合的系数可以通过PCA计算出来。

步骤3：数据集成

实体识别
冗余属性识别
数据变化
简单函数变化
数据标准化
连续数据离散化
属性构造
小波变化
判断是否改变量纲和分布

步骤4：数据规约

步骤5：数据验证

相关性分析-xmind
正态性检验
一致性检验

步骤6：特征选择

分两种情况，小数据集和大数据集。在大数据量的情况下，将数据集分为训练集和测试集，然后在训练数据上进行学习，挑选不同的特征，选择在测试集上表现最好的。具体来说就两种方式，一种是逐步向前，一种是逐步向后。所谓逐步向前，是说一次丢一个特征进去，然后看测试结果有没有变得更好，如果没有，就不放；逐步向
后呢，就是先全部丢进去，然后一次删掉一个，看下有没有变差，如果变差了，这个特征就保留下来。要注意的是，这一步前提：做好了数据审查和清洗才可以做的。
小数据量的时候，比如一个抽样调查的问卷，样本比较少，如果划分成训练和测试集，会使
得模型训练的效果不好，这个时候就不适合刚才说的逐步法，这个时候一般是借助假设检验的方
法，看P值。检验的原假设是假设自变量和因变量没有关系。

sklearn中总结的衡量指标