多目标优化_学习笔记（三）MOEA/D

前言

本篇博客出于学习交流目的，主要是用来记录自己学习多目标优化中遇到的问题和心路历程，方便之后回顾。过程中可能引用其他大牛的博客，文末会给出相应链接，侵删！

REMARK：本人纯小白一枚，如有理解错误还望大家能够指出，相互交流。也是第一次以博客的形式记录，文笔烂到自己都看不下去，哈哈哈

---

笔记（二）记录基于Pareto支配的优化算法，在笔记（三）中记录在学习MOEA/D算法（包括对Tchebycheff聚合方法的理解，比较详细），MOEA/D也是我的直接目标，以为参考的那篇论文用到了这个论文的思想，因为对这个领域一点不了解，就有了前面两个笔记。（一些在第一篇提到的概念这篇就不再重复了）

正文

基于分解的多目标进化算法（MOEA/D）2007年由Qingfu Zhang等人提出。该算法将传统多目标问题转化成为多个单目标问题，对它们同时优化，该算法需要具备一定Pareto基础知识，可回顾多目标优化_学习笔记（一）。

MOEA/D特性：

1. 引入分解的概念，简单但是有效；
2. 由于算法将MOP问题分解成子问题（单维度）进行计算，适配度分配和多样性控制的难度都有所降低；
3. 相较NSGA-II和MOGLS算法MOEA/D具有更低的计算复杂度，但在许多场景下解得表现上更为出色；
4. 弥补传统不是基于分解的算法难以找到一个简单方法来利用标量（单维度）优化算法的缺点；

三种分解算法

一般将MOP多目标转换到一组标量优化问题常用的分解方法有权重求和法；切比雪夫聚合方法；边界交叉聚合方法。下面会一一解释这些方法，MOEA/D采用切比雪夫聚合方法，也可以只看这一部分。

---

A、权重求和法（Weighted Sum Approach ）
常用的权重求和公式为（最小化）：

mingws(x|λ⃗ )=∑i=1mλifi(x) m i n g w s ( x | λ → ) = ∑ i = 1 m λ i f i ( x )

s.t.x∈Ω s . t . x ∈ Ω

其中，待优化的目标分量有 m m 个， λ⃗ =(λ1，λ2，⋯，λm) λ → = ( λ 1 ， λ 2 ， ⋯ ， λ m ) 是的权值向量，每个权值分量 λi λ i 分别对应第 i i 个目标分量；限制条件 λi≥0 λ i ≥ 0 && ∑mi=1λi=1 ∑ i = 1 m λ i = 1 （如二维坐标，保证等高线斜率为 [−0，−∞] [ − 0 ， − ∞ ] ）。 文章给出了利用线性加权法求Pareto解得图例，可以看下链接中的图例，有助于理解等高线（等值线）概念。 利用这个方法可将多目标问题转换成单个数值目标函数，但在寻找非凸解得问题上难度大。

B、切比雪夫聚合方法（Tchebycheff Approach）

mingte(x|λ,z∗)=max{λi(fi(x)−z∗i)} m i n g t e ( x | λ , z ∗ ) = m a x { λ i ( f i ( x ) − z i ∗ ) }

s.t.x∈Ω s . t . x ∈ Ω

其中， z∗=(z∗1，⋯，z∗i) z ∗ = ( z 1 ∗ ， ⋯ ， z i ∗ ) T T ，对于每一个目标分量 i i ， z∗i=min{fi(x)|x∈Ω} z i ∗ = m i n { f i ( x ) | x ∈ Ω } ，即每个目标分量最小值组成的坐标。

下面给出图例用于理解这个公式，首先感谢两篇博客，通过他们的分享给了我很大的启发，但是由于有些理解上的不同，下面给出我自己的理解，如有错误还请大家指正。

Chithonhttp://blog.csdn.net/qithon/article/details/72885053#comments
jinTesterhttp://blog.csdn.net/jinjiahao5299/article/details/76045936

针对我的理解和前人给出的图例我重新画了一个图，帮助理解。

以二目标最小优化问题为例，我们令 f′i(x)=fi(x)−z∗i f i ′ ( x ) = f i ( x ) − z i ∗ ，如图所示坐标系从 fi f i 变换到 f′i f i ′ ，这个过程对应定义很容易理解，之后的操作都针对这个变换后的坐标系;那么公式变为 mingte(x|λ)=max{λif′i(x)} m i n g t e ( x | λ ) = m a x { λ i f i ′ ( x ) } ，可以看出这个公式和线性加权的很像，只是线性加权是求和，而切比雪夫方法是比较最大值。

现在我们给定一个 λ⃗  λ → ，如图紫线所示；我们的目标是要找到Pareto前沿面PF（红线）上的个体（点），给定 λ⃗  λ → 之后，对位于 λ⃗  λ → 上方的个体衡有 f′1λ1>f′2λ2 f 1 ′ λ 1 > f 2 ′ λ 2 ，即 mingte(x|λ,z∗)=f′1λ1 m i n g t e ( x | λ , z ∗ ) = f 1 ′ λ 1 ，无论 f′2 f 2 ′ 取值如何变化，只要 f′1 f 1 ′ 不变，结果大小都一样，所以等高线是平行于 f′2 f 2 ′ 的一条直线，同理可推位 λ⃗  λ → 下方等高线是平行于 f′1 f 1 ′ 的一条直线，两条直线组合成为等高线（橙色），且等高线上的个体评估值与等高线交于 λ⃗  λ → 的点取值相同。

下面是收敛过程，上面已经讲解了等高线为什么是由两条垂直的线组成，同样可以用来说明收敛过程，在位于 λ⃗  λ → 上方的个体，如果出现新的个体 f′1 f 1 ′ 小于等高线值，则等高线向下移动（注意两条线同时移动）；同理，位于 λ⃗  λ → 下方的个体，如果出现新的个体 f′2 f 2 ′ 小于等高线值，则等高线向左移动（注意两条线同时移动），直到搜索到Pareto前沿。

当我们对 λ⃗  λ → 取不同值（如 λ′→ λ ′ → ），就可以得到其他Pareto解。

文中还提到了一个权重切比雪夫聚合方法，就是结合两种方法并加了个参数 ρ ρ 控制两种方法的比例。思想比较简单直接给公式：

mingte(x|λ,z∗)=max{λi(fi(x)−z∗i)}+ρ∑j=1m(fj(x)−z∗j) m i n g t e ( x | λ , z ∗ ) = m a x { λ i ( f i ( x ) − z i ∗ ) } + ρ ∑ j = 1 m ( f j ( x ) − z j ∗ )

s.t.x∈Ω s . t . x ∈ Ω

Chithon的博客中提到标准Tchebycheff Approach得到的解不均匀，Yutao Qi等人于2014年提出一种解决方法(MOEA/D with Adaptive Weight Adjustment)，

λ∗=(1λ1∑mi=11λi,....,1λm∑mi=11λi) λ ∗ = ( 1 λ 1 ∑ i = 1 m 1 λ i , . . . . , 1 λ m ∑ i = 1 m 1 λ i )

通过这个参照向量的转换即可得到分布均匀的解。

C、边界交叉聚合方法（penalty-based boundary intersection (PBI) approach）
最初的边界交叉方法给出公式如下：

mingbi(x|λ,z∗)=d m i n g b i ( x | λ , z ∗ ) = d

s.t.x∈Ω s . t . x ∈ Ω

z∗−F(x)=dλ z ∗ − F ( x ) = d λ

给个文中的图例，其中， λ,z∗ λ , z ∗ 和上个方法切比雪夫中的定义一致（ 最大优化问题，只是的 z∗ z ∗ 最大最小变了一下），约束条件 z∗−F(x)=dλ z ∗ − F ( x ) = d λ ，需要保证 F(x) F ( x ) 与 λ λ 在同一直线上，这个限制条件不太现实，所以做出来改进。其中， d d 为标量，表示 F(x) F ( x ) 在 λ λ 方向上的距离，越小表示越优。

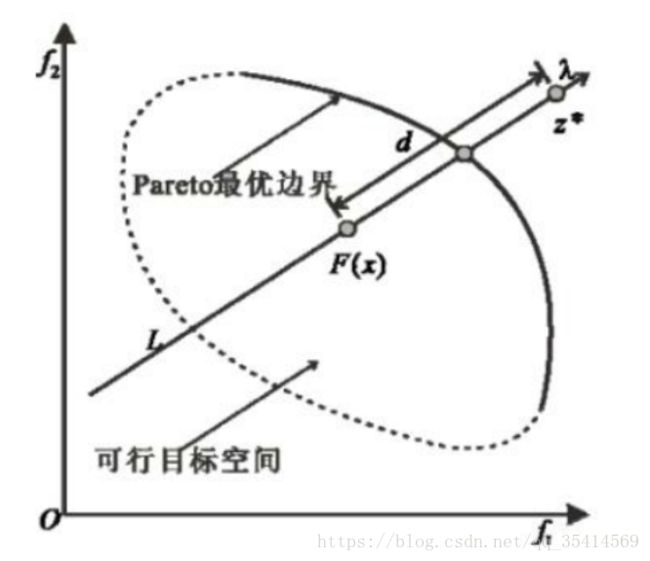
>>> penalty-basedboundary intersection approach
基于惩罚的边界交叉方法：

mingbip(x|λ,z∗)=d1+θd2 m i n g b i p ( x | λ , z ∗ ) = d 1 + θ d 2

s.t.x∈Ω s . t . x ∈ Ω

d1=∣∣(z∗−F(x))Tλ∣∣|λ| d 1 = | ( z ∗ − F ( x ) ) T λ | | λ |

d2=|F(x)−(z∗−d1λ)| d 2 = | F ( x ) − ( z ∗ − d 1 λ ) |

作为对上一个算法的改进，改为添加惩罚函数进行处理约束。 θ>0 θ > 0 是一个预设参数，通常取0.5。 d1 d 1 为标量，表示 F(x) F ( x ) 在 λ λ 方向上投影的距离； d2 d 2 为惩罚值（标量），表示 F(x) F ( x ) 在 λ λ 方向上 垂直投影的距离，偏离 λ λ 越远，惩罚值越大。

在超过两个目标时，PBI方法比切比雪夫聚合方法能够获得的最优解分布更加均匀，尤其是在目标较少的情况下，这种现象更加明显。

整体框架

下面是中午原文中的算法流程图，我们按这个思路理解。


算法主要思想在于，若 λj λ j 与 λj λ j 相邻，那么 gte(x∣λj,z∗) g t e ( x ∣ λ j , z ∗ ) 与 gte(x∣λj,z∗) g t e ( x ∣ λ j , z ∗ ) 也应该非常相近。

算法细节上的理解
输入输出很好理解，我们直接看算法步骤 ↓

Step1：初始化
1)计算权重向量之间的欧式距离，对于每个权重向量 λi λ i 得到离它最近的T个权重向量存在 B(i) B ( i ) （相邻集合）中，画了一个简要图，便于理解，注意 λi λ i 的取值范围 ∑mi=1λi=1 ∑ i = 1 m λ i = 1 (这里 m=2 m = 2 )，所以向量终端一定在橙线（ y=−x+1 y = − x + 1 ）上，所以欧式距离越小，表示越相邻；

2)随机生成初始种群 x1,⋯,xN x 1 , ⋯ , x N ；

3)初始化 z∗→=(z1,⋯,zm)T z ∗ → = ( z 1 , ⋯ , z m ) T ， zi=min{fi(x1),fi(x2),⋯fi(xN)} z i = m i n { f i ( x 1 ) , f i ( x 2 ) , ⋯ f i ( x N ) } ,即每个目标分量上的最大值或最小值（视优化问题而定，这里是最小化优化）；

4)创建一个外部种群（EP）用于存储过程优秀个体，初始为空。

Step2：种群更新
对于每个 i i 都做以下操作:

1)从邻集 B(i) B ( i ) 中随机取两个序号 k,l k , l 利用基因重组遗传算子让 xk x k 和 xl x l 产生新解 y y ；

2)对 y y 运用基于测试你问题的修复和改进启发产生 y, y , ;

对0/1背包问题
在随机生成解得同时，我们有可能获得一个没有完全符合解约束的解，这时候需要进行修复

k=argminj∈Jg(y)−g(yj−)∑i∈Iwij k = a r g m i n j ∈ J g ( y ) − g ( y j − ) ∑ i ∈ I w i j

可利用上式修复， g g 为目标函数，如果分母影响最大同时又对分子影响最小的y存在，那么我们将这个y从解中去掉，反复循环，可知当前解符合要求。

3)更新 z∗→ z ∗ → ，判断 y, y , 是否可能替换原有极值；

4)更新领域解 B(i) B ( i ) ，对于领域中每个权值向量 λj λ j ，如果得到优化，则更新；

5)更新外部种群EP，从EP中移除所有被 F(y,) F ( y , ) 支配的解，如果不存在这的解，则将 F(y,) F ( y , ) 加入EP中。

Step3：条件终止
根据停止条件停止，停止并输出EP，否则重复步骤2。

结论

MOEA/D相比于NSGA-II和MOGLS有较低的计算复杂度，同时解得质量又很高；可以解决不连续优化问题；对T参数不敏感，且计算成本是线性增长。——中文原文

---

最后任然要感谢以下博客对我的帮助
多目标优化系列（三）MOEA/D
多目标优化算法的理解：线性加权法
多目标进化算法(MOEA)概述
多目标优化问题中常见分解方法的理解

MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition
中文链接：https://wenku.baidu.com/view/d163a04d915f804d2a16c102.html