数学建模 | MATLAB学习 | 插值 一维插值函数、三次样条插值

1.一维插值函数

Matlab中有现成的一维插值函数interp1，语法为

 y=interp1(x0,y0,x,'method')

x0,y0是已知的数据向量，其中x应以升序或者降序排列（所有的插值方法要求x0是单调的），x1是插值点的自变量坐标向量；

其中method指定插值的方法，默认为线性插值。其值可为

 'nearest'   最近项插值 'linear'    线性插值 'spline'    立方样条插值 'cubic'    立方插值

当x0为等距时可以用快速插值法，使用快速插值法的格式为'*nearest'、'*linear'、'*spline'、'*cubic'。

实例：

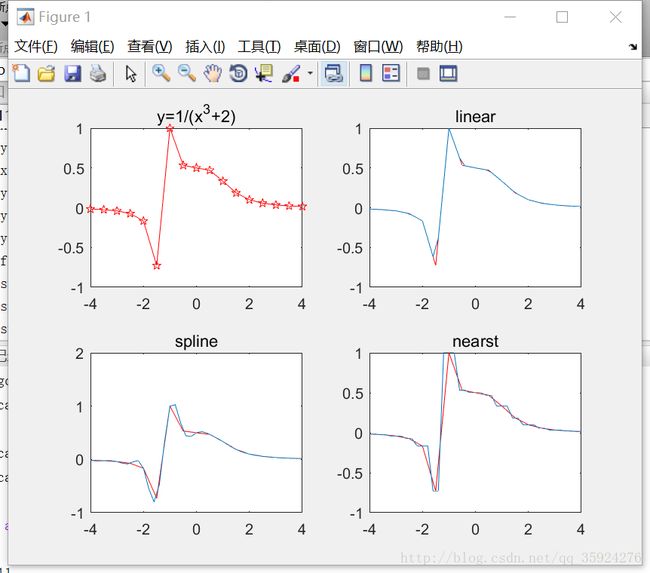
y=1/（x^3+2）  -4<=x<=4  用13个节点作三种插值，并比较结果。

在MATLAB中新建脚本，代码如下：

x0=-4:0.5:4;
y0=1./(2+x0.^3);
x=-4:0.2:4;
y1=interp1(x0,y0,x,'linear');
y2=interp1(x0,y0,x,'spline');
y3=interp1(x0,y0,x,'nearst');
subplot(2,2,1),plot(x0,y0,'r-p');title('y=1/(x^3+2)');%suplot一个窗口显示多个图形，并排版
subplot(2,2,2),plot(x0,y0,'r-',x,y1);title('linear');
subplot(2,2,3),plot(x0,y0,'r-',x,y2);title('spline');
subplot(2,2,4),plot(x0,y0,'r-',x,y3);title('nearst');

保存并运行，得到如下：

2.三次样条插值

 在Matlab中数据点称之为断点。如果三次样条插值没有边界条件，最常用的方法，就是采用非扭结（not-a-knot）条件。这个条件强迫第1个和第2个三次多项式的三阶导数相等。对最后一个和倒数第2个三次多项式也做同样地处理。

 

Matlab中三次样条插值spline有如下函数

 y=interp1(x0,y0,x,'spline')；

 y=spline(x0,y0,x)；

 pp=csape(x0,y0,conds)；

 pp=csape(x0,y0,conds,valconds)；y=ppval(pp,x)；

其中x0,y0是已知数据点，x是插值点，y是插值点的函数值。

 

对于三次样条插值，提倡使用函数csape，csape的返回值是pp形式，要求插值点的函数值，必须调用函数ppval。

pp=csape(x0,y0)使用默认的边界条件，即Lagrange边界条件。

pp=csape(x0,y0,conds,valconds)中的conds指定插值的边界条件，其值可为

'complete'    边界为一阶导数，一阶导数的值在valconds参数中给出，若忽略valconds参数，则按缺省情况处理。

'not-a-knot'   非扭结条件。

'periodic'     周期条件。

'second'      边界为二阶导数，二阶导数的值在valconds参数中给出，若忽略valconds参数，二阶导数的缺省值为[0, 0]。

'variational'   设置边界的二阶导数值为[0,0]。

对于一些特殊的边界条件，可以通过conds的一个矩阵来表示，conds元素的取值为0，1，2。

conds(i)=j的含义是给定端点的阶导数，即conds的第一个元素表示左边界的条件，第二个元素表示右边界的条件，conds=[2,1]表示左边界是二阶导数，右边界是一阶导数，对应的值由valconds给出。

详细情况请使用帮助doccsape。

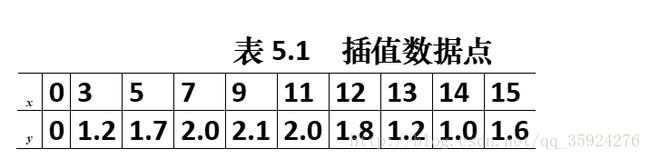
实例1 ：

x0=[0   3   5   7   9   11   12   13   14  15];
y0=[0  1.2  1.7  2.0  2.1  2.0  1.8  1.2   1.0  1.6];
x=0:0.1:15;
y1=interp1(x0,y0,x);
y2=interp1(x0,y0,x,'spline');
pp1=csape(x0,y0);
y3=ppval(pp1,x);
pp2=csape(x0,y0,'second');
y4=ppval(pp2,x);
[x',y1',y2',y3',y4']
subplot(1,3,1)
plot(x0,y0,'+',x,y1)
title('Piecewise linear')
subplot(1,3,2)
plot(x0,y0,'+',x,y2)
title('Spline1')
subplot(1,3,3)
plot(x0,y0,'+',x,y3)
title('Spline2')
dx=diff(x);
dy=diff(y3);
dy_dx=dy./dx;
dy_dx0=dy_dx(1)
ytemp=y3(131:151);
ymin=min(ytemp);
index=find(y3==ymin);
xmin=x(index);
[xmin,ymin]

实例2：

代码如下：

x0=0.15:0.01:0.18;
y0=[3.5	1.5	2.5	2.8];
pp=csape(x0,y0)   %默认的边界条件，Lagrange边界条件
format long g
xishu=pp.coefs   %显示每个区间上三次多项式的系数
s=quadl(@(t)ppval(pp,t),0.15,0.18)  %求积分
format  %恢复短小数的显示格式

程序运行后得到：

xishu =

         -616666.666666667                     33500         -473.333333333334                       3.5
         -616666.666666667                     15000          11.6666666666671                       1.5
         -616666.666666668         -3499.99999999999          126.666666666667                       2.5


s =

                  0.068625