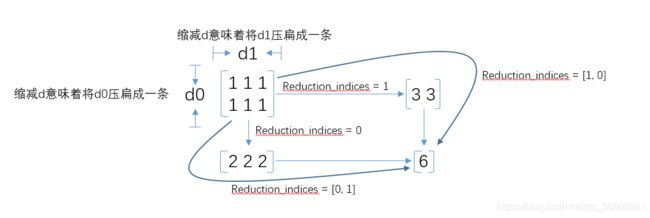
tensorflow中reduction_indices参数的降维作用

最近在学习TensorFlow，在看莫烦的网课，对如下代码中loss函数产生了疑问。

import tensorflow as tf
import numpy as np


def addlayer(inputs, insize, outsize, activation_function=None):
    Weights = tf.Variable(tf.random_normal([insize, outsize]))  # 定义权值矩阵，一般初始值为随机数比赋全0要好
    biases = tf.Variable(tf.zeros(outsize) + 0.1)  # 在机器学习中，biases的推荐值不为0，所以我们这里是在0向量的基础上又加了0.1
    Wx_plus_b = tf.matmul(inputs, Weights) + biases  # 此处矩阵乘的顺序一定要注意！！！
    if activation_function is None:  # 注意此处使用is
        output = Wx_plus_b
    else:
        output = activation_function(Wx_plus_b)
    return outpu

x_data = np.linspace(-1, 1, 300, dtype=np.float32)[:, np.newaxis]
noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32)
y_data = np.square(x_data) - 0.5 + noise

xs = tf.placeholder(tf.float32, [None, 1])  # 输入只有一个特征
ys = tf.placeholder(tf.float32, [None, 1])

l1 = addlayer(xs, 1, 10, activation_function=tf.nn.relu)  # 隐层的输入为1（特征数），输出定义为10个神经元
prediction = addlayer(l1, 10, 1, None)  # 输出层为1，不需要激活函数

loss = tf.reduce_mean(tf.reduce_sum(tf.square(prediction-ys), reduction_indices=[1]))
# tf.reduce_sum()这一步相当于降维了（原来的二维数组变为了一维数组），，最后可以求一维数组的平均值
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
for i in range(1000):
    sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
    if i % 100 == 0:
        print(sess.run(loss, feed_dict={xs: x_data, ys: y_data}))

这其中，我对 loss = tf.reduce_mean(tf.reduce_sum(tf.square(prediction-ys) 不是很懂，特别是tf.reduce_sum()函数。于是我在写了一个小例子就一目了然了。

a=np.linspace(0,4,5)[:,np.newaxis]
b=np.linspace(1,5,5)[:,np.newaxis]
c=tf.square(b-a)
d = tf.reduce_sum(c, reduction_indices=[1])
e=tf.reduce_mean(d）
with tf.Session() as sess:
    print("c:",sess.run(c),"d:",sess.run(d)，"e:",sess.run(e))

上面的代码中[:,np.newaxis]表示的是一个升维的过程，此例中是将一个一位数组升维到一个行扩展的二维数组，即a=[[0],[1],[2],[3],[4]]。原来1行1列的一维数组变成了4行1列的矩阵。
上面小例子的结果为：
c: [[1.]
[1.]
[1.]
[1.]
[1.]]

d: [1. 1. 1. 1. 1.]

e: 1.0

上面小例子的 c 为5行1列的二维矩阵变成了 d（一维数组）。即 tf.reduce_sum(c, reduction_indices=[1]) 表示的是将列的维度降维（将各列对应元素相加）。
若tf.reduce_sum(c, reduction_indices=[0])，将各行对应元素相加，直接输出 [5] 。 如下图：