泊松融合-Possion Blending

  最近事情比较多，很多之前捣鼓过的东西也没有去进行一个很好的整理，马上又要进入毕业开题的节奏，机器学习也没有一个很好的掌握，泊松融合是之前很久研究了一段时间，说句实话，里面的数学确实复杂，我没有深入，再加之最后我跑的结果实在是太慢，最近小波多聚焦融合的代码也实现，后面会更新。

主要参考博客1：http://eric-yuan.me/poisson-blending/
主要参考博客2:http://blog.csdn.net/hjimce/article/details/45716603
主要参考博客3:http://blog.csdn.net/wd1603926823/article/details/49867069
主要参考博客4：http://blog.csdn.net/baimafujinji/article/details/46787837

关于图像融合
  作为图像融合方法，我们的目标是将源图像中的对象或纹理无缝融合到目标图像中，这里是一个例子：

我们打算把第一张图像中的狗（或熊？），第二张图像中的两个孩子放入第三张图像中的区域。最简单的方法是将第一张和第二张图像的像素复制并粘贴到第三张图像中，结果如下所示：

奇怪的是，在这些地区我们可以看到非常明显的差异，因为这三个来源的水的颜色是不同的，即使背景相匹配，我们也可以看到这些地区之间的接缝。为什么？

  我们的人的视觉比图像的整体强度对梯度更敏感，也就是说，我们不知道每个像素的确切值，但是如果值在某处变化，我们可以很容易地知道它的变化，事实上，导致我们的目标：克隆到另一个图像的像素，但让颜色不会突然改变，即最大限度地保留源区域的梯度。这个结果比上面的要好得多：

泊松混合概述
泊松混合是梯度域图像处理方法之一，也许下面的图片可以很好的
解释：

• v - 图像中某个区域的渐变（作为矢量）
• g - 选定区域的来源（狗熊，儿童…）
• f * - 域S中存在的已知函数（上面第三个源中的水）
• f - 存在于域Ω中的未知函数
• Ω - 现在放在域S上的区域g（目标背景）
• ∂Ω - 源区域和目标区域之间的边界

所以其实我们要做的只不过是给定矢量场v，找出优化的未知区域f的值。

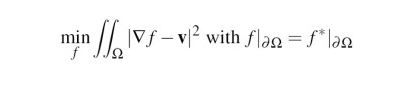
其解是泊松方程的解:


其中div v = ∂v/∂x+∂v/∂y， 是梯度场的发散性质，Δ是拉普拉斯算子：

将拉普拉斯算子应用于泊松方程，我们可以得到：

div G = -4 f(x,y) + f(x-1,y) + f(x,y-1) + f(x+1,y) + f(x,y+1)

1-D EXAMPLE

假设我们要将左图像（4，3，5，4）的红色部分复制到右图像中。
  首先，我们得到了上左图的渐变（梯度），如图中红色条形上方数值所示，现在我们将这些像素移动到右手边的图像上，而不会突然改变值，所以我们要：

我们可以发现，上面的矩阵是核（-2 4 -2）的卷积，因为每个像素值都受到两个相邻像素的影响，这与2D情况下的拉普拉斯算子非常相似，每个像素值都受到影响由四个相邻的像素（上，下，左，右）来确定。

2-D EXAMPLE

假设我们要将一些像素复制到上面图像的白色区域（红色像素是边界像素），我们通过使用与1D情况相同的方程来进行：

Ax = b
其中 A是一个N×N矩阵，N是我们要复制的像素的数量，在这种情况下，N = 10。

for i=1:row number
    for j=1:col number
        if(i==j)
            matrix(i, j)=-4
        elif(adjacent(pixel(j), pixel(i)))
            matrix(i, j)=1
        else
            matrix(i, j)=0
        end
    end
end

所以在这种情况下矩阵是这样的：

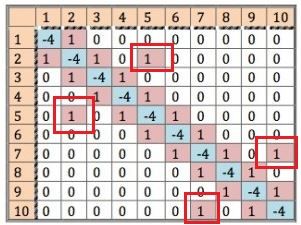
(备注：)我个人觉得有上述代码的不出来我圈出来的四个红色方框的值，可能是我理解有问题，有明白的朋友望告知。

在这个等式中，b是一个N元素矢量，并且由下式创建：

b[i] = div ( G( Source(x,y) ) ) + Neighbor(target i) ; i=1..N
div v 可以用本文前面的公式计算，Neighbour意味着像素i的4个邻居属于边界，例如：
Neighbor(pixel 1) are pixels left, up, right;
Neighbor(pixel 8) are pixels left, up;
Neighbor(pixel 5) is pixels up.

如果我们知道矩阵A和向量b，就可以计算向量x，它是目标图像内像素的值。

x = A \ b（’\’表示矩阵左除）
或者x = A -1 * b

这篇文章基本上就是第一篇博客抄录过来的，里面还提到关于泊松方程快速解法的相关知识，我也没去研究，不做详细说明。
博主链接已给出，快速解法链接如下：
点我开始跳转

3.Code

测试代码如下：

// Poisson Blending
// Using stupid way (just solving Ax = b)
// Author: Eric Yuan
// Blog: http://eric-yuan.me
// You are free to use the following code for ANY purpose.
// 
// You can improve it by using advanced methods, 
// About solving discrete Poisson Equation using Jacobi, SOR, Conjugate Gradients, and FFT
// see here: http://www.cs.berkeley.edu/~demmel/cs267/lecture24/lecture24.html
// 

#include "opencv2/core/core.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include 
#include 
#include 

using namespace cv;
using namespace std;

#define elif else if
#define ATD at


// calculate horizontal gradient, img(i, j + 1) - img(i, j)
Mat 
    getGradientXp(Mat &img){
        int height = img.rows;
        int width = img.cols;
        Mat cat = repeat(img, 1, 2);

        Rect roi = Rect(1, 0, width, height);
        Mat roimat = cat(roi);
        return roimat - img;
}

// calculate vertical gradient, img(i + 1, j) - img(i, j)
Mat 
    getGradientYp(Mat &img){
        int height = img.rows;
        int width = img.cols;
        Mat cat = repeat(img, 2, 1);

        Rect roi = Rect(0, 1, width, height);
        Mat roimat = cat(roi);
        return roimat - img;
}

// calculate horizontal gradient, img(i, j - 1) - img(i, j)
Mat 
    getGradientXn(Mat &img){
        int height = img.rows;
        int width = img.cols;
        Mat cat = repeat(img, 1, 2);

        Rect roi = Rect(width - 1, 0, width, height);
        Mat roimat = cat(roi);
        return roimat - img;
}

// calculate vertical gradient, img(i - 1, j) - img(i, j)
Mat 
    getGradientYn(Mat &img){
        int height = img.rows;
        int width = img.cols;
        Mat cat = repeat(img, 2, 1);

        Rect roi = Rect(0, height - 1, width, height);
        Mat roimat = cat(roi);
        return roimat - img;
}

int
    getLabel(int i, int j, int height, int width){
        return i * width + j;
}

// get Matrix A.
Mat
    getA(int height, int width){

        Mat A = Mat::eye(height * width, height * width, CV_64FC1);
        A *= -4;
        Mat M = Mat::zeros(height, width, CV_64FC1);
        Mat temp = Mat::ones(height, width - 2, CV_64FC1);
        Rect roi = Rect(1, 0, width - 2, height);
        Mat roimat = M(roi);
        temp.copyTo(roimat);
        temp = Mat::ones(height - 2, width, CV_64FC1);
        roi = Rect(0, 1, width, height - 2);
        roimat = M(roi);
        temp.copyTo(roimat);
        temp = Mat::ones(height - 2, width - 2, CV_64FC1);
        temp *= 2;
        roi = Rect(1, 1, width - 2, height - 2);
        roimat = M(roi);
        temp.copyTo(roimat);

        for(int i=0; ifor(int j=0; jint label = getLabel(i, j, height, width);
                if(M.ATD(i, j) == 0){
                    if(i == 0)  A.ATD(getLabel(i + 1, j, height, width), label) = 1;
                    elif(i == height - 1)   A.ATD(getLabel(i - 1, j, height, width), label) = 1;
                    if(j == 0)  A.ATD(getLabel(i, j + 1, height, width), label) = 1;
                    elif(j == width - 1)   A.ATD(getLabel(i, j - 1, height, width), label) = 1;
                }elif(M.ATD(i, j) == 1){
                    if(i == 0){
                        A.ATD(getLabel(i + 1, j, height, width), label) = 1;
                        A.ATD(getLabel(i, j - 1, height, width), label) = 1;
                        A.ATD(getLabel(i, j + 1, height, width), label) = 1;
                    }elif(i == height - 1){
                        A.ATD(getLabel(i - 1, j, height, width), label) = 1;
                        A.ATD(getLabel(i, j - 1, height, width), label) = 1;
                        A.ATD(getLabel(i, j + 1, height, width), label) = 1;
                    }
                    if(j == 0){
                        A.ATD(getLabel(i, j + 1, height, width), label) = 1;
                        A.ATD(getLabel(i - 1, j, height, width), label) = 1;
                        A.ATD(getLabel(i + 1, j, height, width), label) = 1;
                    }elif(j == width - 1){
                        A.ATD(getLabel(i, j - 1, height, width), label) = 1;
                        A.ATD(getLabel(i - 1, j, height, width), label) = 1;
                        A.ATD(getLabel(i + 1, j, height, width), label) = 1;
                    }
                }else{
                    A.ATD(getLabel(i, j - 1, height, width), label) = 1;
                    A.ATD(getLabel(i, j + 1, height, width), label) = 1;
                    A.ATD(getLabel(i - 1, j, height, width), label) = 1;
                    A.ATD(getLabel(i + 1, j, height, width), label) = 1;
                }
            }
        }
        return A;
}

// Get the following Laplacian matrix
// 0  1  0
// 1 -4  1
// 0  1  0
Mat
    getLaplacian(){
        Mat laplacian = Mat::zeros(3, 3, CV_64FC1);
        laplacian.ATD(0, 1) = 1.0;
        laplacian.ATD(1, 0) = 1.0;
        laplacian.ATD(1, 2) = 1.0;
        laplacian.ATD(2, 1) = 1.0;
        laplacian.ATD(1, 1) = -4.0; 
        return laplacian;
}

// Calculate b
// using convolution.
Mat
    getB1(Mat &img1, Mat &img2, int posX, int posY, Rect ROI){
        Mat Lap;
        filter2D(img1, Lap, -1, getLaplacian());
        int roiheight = ROI.height;
        int roiwidth = ROI.width;
        Mat B = Mat::zeros(roiheight * roiwidth, 1, CV_64FC1);
        for(int i=0; ifor(int j=0; jdouble temp = 0.0;
                temp += Lap.ATD(i + ROI.y, j + ROI.x);
                if(i == 0)              temp -= img2.ATD(i - 1 + posY, j + posX);
                if(i == roiheight - 1)  temp -= img2.ATD(i + 1 + posY, j + posX);
                if(j == 0)              temp -= img2.ATD(i + posY, j - 1 + posX);
                if(j == roiwidth - 1)   temp -= img2.ATD(i + posY, j + 1 + posX);
                B.ATD(getLabel(i, j, roiheight, roiwidth), 0) = temp;
            }
        }
        return B;
}

// Calculate b
// using getGradient functions.
Mat
    getB2(Mat &img1, Mat &img2, int posX, int posY, Rect ROI){
        Mat grad = getGradientXp(img1) + getGradientYp(img1) + getGradientXn(img1) + getGradientYn(img1);
        int roiheight = ROI.height;
        int roiwidth = ROI.width;
        Mat B = Mat::zeros(roiheight * roiwidth, 1, CV_64FC1);
        for(int i=0; ifor(int j=0; jdouble temp = 0.0;
                temp += grad.ATD(i + ROI.y, j + ROI.x);
                if(i == 0)              temp -= img2.ATD(i - 1 + posY, j + posX);
                if(i == roiheight - 1)  temp -= img2.ATD(i + 1 + posY, j + posX);
                if(j == 0)              temp -= img2.ATD(i + posY, j - 1 + posX);
                if(j == roiwidth - 1)   temp -= img2.ATD(i + posY, j + 1 + posX);
                B.ATD(getLabel(i, j, roiheight, roiwidth), 0) = temp;
            }
        }
        return B;
}

// Solve equation and reshape it back to the right height and width.
Mat
    getResult(Mat &A, Mat &B, Rect &ROI){
        Mat result;
        solve(A, B, result);
        result = result.reshape(0, ROI.height);
        return  result;
}



// img1: 3-channel image, we wanna move something in it into img2.
// img2: 3-channel image, dst image.
// ROI: the position and size of the block we want to move in img1.
// posX, posY: where we want to move the block to in img2

Mat
    poisson_blending(Mat &img1, Mat &img2, Rect ROI, int posX, int posY){

        int roiheight = ROI.height;
        int roiwidth = ROI.width;
        Mat A = getA(roiheight, roiwidth);

        // we must do the poisson blending to each channel.
        vector rgb1;
        split(img1, rgb1);
        vector rgb2;
        split(img2, rgb2);

        vector result;
        Mat merged, res, Br, Bg, Bb;
        // For calculating B, you can use either getB1() or getB2()
        Br = getB1(rgb1[0], rgb2[0], posX, posY, ROI);
        //Br = getB2(rgb1[0], rgb2[0], posX, posY, ROI);
        res = getResult(A, Br, ROI);
        result.push_back(res);
        cout<<"R channel finished..."<1], rgb2[1], posX, posY, ROI);
        //Bg = getB2(rgb1[1], rgb2[1], posX, posY, ROI);
        res = getResult(A, Bg, ROI);
        result.push_back(res);
        cout<<"G channel finished..."<2], rgb2[2], posX, posY, ROI);
        //Bb = getB2(rgb1[2], rgb2[2], posX, posY, ROI);
        res = getResult(A, Bb, ROI);
        result.push_back(res);
        cout<<"B channel finished..."<// merge the 3 gray images into a 3-channel image 
        merge(result,merged);
        return merged; 
}

int 
    main(int argc, char** argv)
{
    long start, end;
    start = clock();

    Mat img1, img2;
    Mat in1 = imread("girl.jpg");
    Mat in2 = imread("ocean.jpg");
    imshow("src", in1);
    imshow("dst", in2);
    in1.convertTo(img1, CV_64FC3);
    in2.convertTo(img2, CV_64FC3);

    Rect rc = Rect(92, 40, 55, 90);
    Mat result = poisson_blending(img1, img2, rc, 184, 220);
    result.convertTo(result, CV_8UC1);
    Rect rc2 = Rect(184, 220, 55, 90);
    Mat roimat = in2(rc2);
    result.copyTo(roimat);

    end = clock();
    cout<<"used time: "<<((double)(end - start)) / CLOCKS_PER_SEC<<" second"<"roi", result);
    imshow("result", in2);

    waitKey(0);
    return 0;
}

opencv3已经有相应封装好的类直接调用就好

#include

using namespace cv;
int main()
{
  Mat src = imread("images/015-CT.png");
  Mat dst = imread("images/015-MR-T2.png");
  if(src.empty()||dst.empty())
  {
    return 0;
  }

  Mat src_mask = 255 * Mat::ones(src.rows, src.cols, src.depth());

  Point center(dst.cols / 2, dst.rows / 2);


  Mat normal_clone;
  Mat mixed_clone;

  seamlessClone(src, dst, src_mask, center, normal_clone, NORMAL_CLONE);
  seamlessClone(src, dst, src_mask, center, mixed_clone, MIXED_CLONE);

  imshow("normal_clone",normal_clone);
  imshow("mixed_clone",mixed_clone);
  waitKey(0);
  return 1;
}

关于最后的效果，并没有论文中展示的那么好
可能与我选取的图片也有关系以及对opencv代码的
理解，不过不得不承认opencv的代码优化确实做的好
，非常的快。