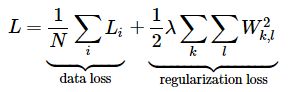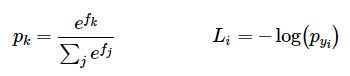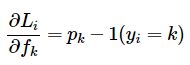python实现循环神经网络RNN
目录
python实现循环神经网络
1 生成一些数据
2 定义激活函数
3 训练Softmax线性分类器
3.1 初始化参数
3.2 计算得分
3.3 计算损失
3.4 用反向传播计算分析梯度
3.5 执行参数更新
3.6 测试训练正确率
4 训练神经网络
4.1 用sigmoid非线性训练网络
4.2 用ReLU非线性训练网络
5 完整代码
python实现循环神经网络
1 生成一些数据
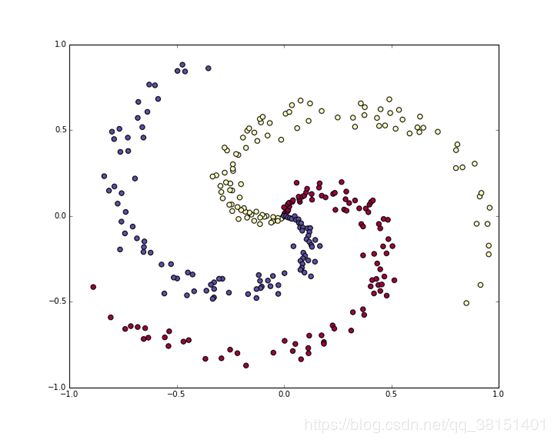
让我们生成一个不易线性分离的分类数据集。我们最喜欢的例子是螺旋数据集,可以按如下方式生成
| #玩具螺旋数据由三个类别(蓝色,红色,黄色)组成,这些类别不是线性可分的。 N = 100 # number of points per class D = 2 # dimensionality K = 3 # number of classes X = np.zeros((N*K,D)) # data matrix (each row = single example) y = np.zeros(N*K, dtype='uint8') # class labels for j in range(K): ix = range(N*j,N*(j+1)) r = np.linspace(0.0,1,N) # radius t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] y[ix] = j # lets visualize the data: plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral) plt.show() |
2 定义激活函数
sigmoid函数“压缩”输入位于0和1之间。不幸的是,这意味着对于sigmoid输出接近0或1的输入,相对于这些输入的梯度接近于零。这导致梯度消失的现象,其中梯度下降接近于零,并且网络不能很好地学习。
另一方面,relu函数(max(0,x))不会随输入大小而饱和。
| #sigmoid函数“压缩”输入位于0和1之间。不幸的是,这意味着对于sigmoid输出接近0或1的输入,相对于这些输入的梯度接近于零。 #这导致梯度消失的现象,其中梯度下降接近于零,并且网络不能很好地学习。 def sigmoid(x): x = 1/(1+np.exp(-x)) return x
def sigmoid_grad(x): return (x)*(1-x)
#relu函数(max(0,x))不会随输入大小而饱和 def relu(x): return np.maximum(0,x) |
3 训练Softmax线性分类器
我们构建一个非常简单的神经网络,有三层(两个隐藏层),您可以换掉ReLU / sigmoid非线性。
定义函数:
| def three_layer_net(NONLINEARITY,X,y, model, step_size, reg): |
3.1 初始化参数
Softmax分类器具有线性分数函数并使用交叉熵损失。线性分类器的参数由权重矩阵W和b每个类的偏置向量组成。
| #parameter initialization h= model['h'] h2= model['h2'] W1= model['W1'] W2= model['W2'] W3= model['W3'] b1= model['b1'] b2= model['b2'] b3= model['b3']
# some hyperparameter # 梯度下降 num_examples = X.shape[0] plot_array_1=[] plot_array_2=[] |
3.2 计算得分
由于这是一个线性分类器,我们可以非常简单地与单个矩阵乘法并行计算所有类别得分:
| for i in range(50000): #前向传播 if NONLINEARITY== 'RELU': hidden_layer = relu(np.dot(X, W1) + b1) hidden_layer2 = relu(np.dot(hidden_layer, W2) + b2) scores = np.dot(hidden_layer2, W3) + b3
elif NONLINEARITY == 'SIGM': hidden_layer = sigmoid(np.dot(X, W1) + b1) hidden_layer2 = sigmoid(np.dot(hidden_layer, W2) + b2) scores = np.dot(hidden_layer2, W3) + b3 |
在这个例子中,我们有300个2-D点,所以在这个乘法之后,数组scores将具有[300 x 3]的大小,其中每行给出对应于3个类(蓝色,红色,黄色)的类分数。
3.3 计算损失
我们需要的第二个关键因素是损失函数,它是一个可微目标,可以量化我们对计算出的班级分数的不满意程度。直观地说,我们希望正确的类比其他类得分更高。在这种情况下,损失应该很低,否则损失应该很高。有很多方法可以量化这种直觉,但是在这个例子中,让我们使用与Softmax分类器相关的交叉熵损失。回想一下,如果f是单个例子的类分数数组(例如这里的3个数数组),那么Softmax分类器计算该例子的损失为:
我们可以看到Softmax分类器将f的每个元素解释为持有这三个类的(非规范化)对数概率。我们将这些取幂得到(非标准化的)概率,然后将它们标准化得到概率。因此,log中的表达式是正确类的归一化概率。注意这个表达式的工作原理:这个量总是在0和1之间。当正确类的概率非常小(接近于0)时,损失将趋于(正)无穷大。相反,当正确的类概率趋近于1时,损失将趋近于零,因为log(1)=0。因此,当正确的类概率高时,Li的表达式值是低的,当正确的类概率低时,Li的表达式值是非常高的。
完整的Softmax分类器损失被定义为训练实例和正则化之间的平均交叉熵损失:
给定我们上面计算的分数数组,我们可以计算损失。首先,得到概率的方法很简单:
- 计算损失:
| #计算损失 #probs大小为[300 x 3] 的数组,其中每行现在包含类概率 exp_scores = np.exp(scores) probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K] |
- 我们现在有一个probs大小为[300 x 3] 的数组,其中每行现在包含类概率。特别是,因为我们已将它们标准化,现在每一行总和为一。我们现在可以在每个示例中查询分配给正确类的对数概率:
| corect_logprobs = -np.log(probs[range(num_examples),y]) data_loss = np.sum(corect_logprobs)/num_examples |
- 该数组correct_logprobs是一维数组,仅包含为每个示例分配给正确类的概率。那么完全损失就是这些对数概率的平均值和正则化损失的和:
| reg_loss = 0.5*reg*np.sum(W1*W1) + 0.5*reg*np.sum(W2*W2)+ 0.5*reg*np.sum(W3*W3) loss = data_loss + reg_loss |
3.4 用反向传播计算分析梯度
我们有一种估算损失的方法,现在我们要把它最小化。我们用梯度下降法。也就是说,我们从随机参数开始,计算损失函数相对于参数的梯度,这样我们就知道应该如何改变参数来减少损失。让我们引入中间变量p,它是(标准化)概率的一个向量。
利用链式法则求得:
假设我们计算的概率是p =[0.2, 0.3, 0.5],正确的类是中间类(概率为0.3)。根据这个推导,得分的梯度为df =[0.2, -0.7, 0.5]. 增加的第一个和最后一个元素得分向量f(错误的分数类),会增加损失(由于积极迹象+ 0.2 + 0.5)不好,因此需增加损失损失,而增加正确的班级分数对损失有负面影响。
| # compute the gradient on scores dscores = probs dscores[range(num_examples),y] -= 1 dscores /= num_examples |
反向传播:
| # BACKPROP HERE dW3 = (hidden_layer2.T).dot(dscores) db3 = np.sum(dscores, axis=0, keepdims=True)
if NONLINEARITY == 'RELU':
#backprop ReLU nonlinearity here dhidden2 = np.dot(dscores, W3.T) dhidden2[hidden_layer2 <= 0] = 0 dW2 = np.dot( hidden_layer.T, dhidden2) plot_array_2.append(np.sum(np.abs(dW2))/np.sum(np.abs(dW2.shape))) db2 = np.sum(dhidden2, axis=0) dhidden = np.dot(dhidden2, W2.T) dhidden[hidden_layer <= 0] = 0
elif NONLINEARITY == 'SIGM':
#backprop sigmoid nonlinearity here dhidden2 = dscores.dot(W3.T)*sigmoid_grad(hidden_layer2) dW2 = (hidden_layer.T).dot(dhidden2) plot_array_2.append(np.sum(np.abs(dW2))/np.sum(np.abs(dW2.shape))) db2 = np.sum(dhidden2, axis=0) dhidden = dhidden2.dot(W2.T)*sigmoid_grad(hidden_layer)
dW1 = np.dot(X.T, dhidden) plot_array_1.append(np.sum(np.abs(dW1))/np.sum(np.abs(dW1.shape))) db1 = np.sum(dhidden, axis=0)
# add regularization dW3+= reg * W3 dW2 += reg * W2 dW1 += reg * W1
#option to return loss, grads -- uncomment next comment grads={} grads['W1']=dW1 grads['W2']=dW2 grads['W3']=dW3 grads['b1']=db1 grads['b2']=db2 grads['b3']=db3 #return loss, grads |
3.5 执行参数更新
现在我们已经计算了梯度我们知道了每个参数如何影响损失函数。我们现在将在负梯度方向进行参数更新,以减少损耗:
| # update W1 += -step_size * dW1 b1 += -step_size * db1 W2 += -step_size * dW2 b2 += -step_size * db2 W3 += -step_size * dW3 b3 += -step_size * db3 |
3.6 测试训练正确率
| # evaluate training set accuracy if NONLINEARITY == 'RELU': hidden_layer = relu(np.dot(X, W1) + b1) hidden_layer2 = relu(np.dot(hidden_layer, W2) + b2) elif NONLINEARITY == 'SIGM': hidden_layer = sigmoid(np.dot(X, W1) + b1) hidden_layer2 = sigmoid(np.dot(hidden_layer, W2) + b2) scores = np.dot(hidden_layer2, W3) + b3 predicted_class = np.argmax(scores, axis=1) print ('training accuracy: %.2f' % (np.mean(predicted_class == y))) |
4 训练神经网络
4.1 用sigmoid非线性训练网络
| N = 100 # number of points per class D = 2 # dimensionality K = 3 # number of classes h=50 h2=50 num_train_examples = X.shape[0]
model={} model['h'] = h # size of hidden layer 1 model['h2']= h2# size of hidden layer 2 model['W1']= 0.1 * np.random.randn(D,h) model['b1'] = np.zeros((1,h)) model['W2'] = 0.1 * np.random.randn(h,h2) model['b2']= np.zeros((1,h2)) model['W3'] = 0.1 * np.random.randn(h2,K) model['b3'] = np.zeros((1,K))
(sigm_array_1, sigm_array_2, s_W1, s_W2,s_W3, s_b1, s_b2,s_b3) = three_layer_net('SIGM', X,y,model, step_size=1e-1, reg=1e-3) |
运行结果:
iteration 0: loss 1.130914
iteration 1000: loss 1.099443
iteration 2000: loss 0.961015
iteration 3000: loss 0.828722
iteration 4000: loss 0.814054
iteration 5000: loss 0.80992
...
iteration 45000: loss 0.471655
iteration 46000: loss 0.470753
iteration 47000: loss 0.469861
iteration 48000: loss 0.468986
iteration 49000: loss 0.468135
training accuracy: 0.96
4.2 用ReLU非线性训练网络
| N = 100 # number of points per class D = 2 # dimensionality K = 3 # number of classes h=50 h2=50 num_train_examples = X.shape[0]
model={} model['h'] = h # size of hidden layer 1 model['h2']= h2# size of hidden layer 2 model['W1']= 0.1 * np.random.randn(D,h) model['b1'] = np.zeros((1,h)) model['W2'] = 0.1 * np.random.randn(h,h2) model['b2']= np.zeros((1,h2)) model['W3'] = 0.1 * np.random.randn(h2,K) model['b3'] = np.zeros((1,K))
(relu_array_1, relu_array_2, r_W1, r_W2,r_W3, r_b1, r_b2,r_b3) = three_layer_net('RELU', X,y,model, step_size=1e-1, reg=1e-3)
|
运行结果:
iteration 0: loss 1.115254
iteration 1000: loss 0.341567
iteration 2000: loss 0.154439
iteration 3000: loss 0.134785
iteration 4000: loss 0.129502
iteration 5000: loss 0.126574
...
iteration 45000: loss 0.112814
iteration 46000: loss 0.112758
iteration 47000: loss 0.112705
iteration 48000: loss 0.112652
iteration 49000: loss 0.112601
training accuracy: 0.99
5 完整代码
| #coding=utf-8 # Setup import numpy as np import matplotlib.pyplot as plt
#sigmoid函数“压缩”输入位于0和1之间。不幸的是,这意味着对于sigmoid输出接近0或1的输入,相对于这些输入的梯度接近于零。 #这导致梯度消失的现象,其中梯度下降接近于零,并且网络不能很好地学习。 def sigmoid(x): x = 1/(1+np.exp(-x)) return x
def sigmoid_grad(x): return (x)*(1-x)
#relu函数(max(0,x))不会随输入大小而饱和 def relu(x): return np.maximum(0,x)
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots plt.rcParams['image.interpolation'] = 'nearest' plt.rcParams['image.cmap'] = 'gray'
# 生成一些数据 # 让我们生成一个不易线性分离的分类数据集。我们最喜欢的例子是螺旋数据集,可以按如下方式生成: #玩具螺旋数据由三个类别(蓝色,红色,黄色)组成,这些类别不是线性可分的。 N = 100 # number of points per class D = 2 # dimensionality K = 3 # number of classes X = np.zeros((N*K,D)) # data matrix (each row = single example) y = np.zeros(N*K, dtype='uint8') # class labels for j in range(K): ix = range(N*j,N*(j+1)) r = np.linspace(0.0,1,N) # radius t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] y[ix] = j # lets visualize the data: plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral) plt.show()
#定义sigmoid和relu函数
#我们构建一个非常简单的神经网络,有三层(两个隐藏层),您可以换掉ReLU / sigmoid非线性。 def three_layer_net(NONLINEARITY,X,y, model, step_size, reg): #NONLINEARITY:表示使用哪种激活函数 #parameter initialization
h= model['h'] h2= model['h2'] W1= model['W1'] W2= model['W2'] W3= model['W3'] b1= model['b1'] b2= model['b2'] b3= model['b3']
# some hyperparameters
# 梯度下降 num_examples = X.shape[0] plot_array_1=[] plot_array_2=[] for i in range(50000): #前向传播 if NONLINEARITY== 'RELU': hidden_layer = relu(np.dot(X, W1) + b1) hidden_layer2 = relu(np.dot(hidden_layer, W2) + b2) scores = np.dot(hidden_layer2, W3) + b3
elif NONLINEARITY == 'SIGM': hidden_layer = sigmoid(np.dot(X, W1) + b1) hidden_layer2 = sigmoid(np.dot(hidden_layer, W2) + b2) scores = np.dot(hidden_layer2, W3) + b3
#计算损失 #probs大小为[300 x 3] 的数组,其中每行现在包含类概率 exp_scores = np.exp(scores) probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]
# compute the loss: average cross-entropy loss and regularization #数组correct_logprobs是一维数组,仅包含为每个示例分配给正确类的概率。那么完全损失就是这些对数概率和正则化损失的平均值 corect_logprobs = -np.log(probs[range(num_examples),y]) data_loss = np.sum(corect_logprobs)/num_examples reg_loss = 0.5*reg*np.sum(W1*W1) + 0.5*reg*np.sum(W2*W2)+ 0.5*reg*np.sum(W3*W3) loss = data_loss + reg_loss if i % 1000 == 0: print ("iteration %d: loss %f" % (i, loss))
# compute the gradient on scores dscores = probs dscores[range(num_examples),y] -= 1 dscores /= num_examples
# BACKPROP HERE dW3 = (hidden_layer2.T).dot(dscores) db3 = np.sum(dscores, axis=0, keepdims=True)
if NONLINEARITY == 'RELU':
#backprop ReLU nonlinearity here dhidden2 = np.dot(dscores, W3.T) dhidden2[hidden_layer2 <= 0] = 0 dW2 = np.dot( hidden_layer.T, dhidden2) plot_array_2.append(np.sum(np.abs(dW2))/np.sum(np.abs(dW2.shape))) db2 = np.sum(dhidden2, axis=0) dhidden = np.dot(dhidden2, W2.T) dhidden[hidden_layer <= 0] = 0
elif NONLINEARITY == 'SIGM':
#backprop sigmoid nonlinearity here dhidden2 = dscores.dot(W3.T)*sigmoid_grad(hidden_layer2) dW2 = (hidden_layer.T).dot(dhidden2) plot_array_2.append(np.sum(np.abs(dW2))/np.sum(np.abs(dW2.shape))) db2 = np.sum(dhidden2, axis=0) dhidden = dhidden2.dot(W2.T)*sigmoid_grad(hidden_layer)
dW1 = np.dot(X.T, dhidden) plot_array_1.append(np.sum(np.abs(dW1))/np.sum(np.abs(dW1.shape))) db1 = np.sum(dhidden, axis=0)
# add regularization dW3+= reg * W3 dW2 += reg * W2 dW1 += reg * W1
#option to return loss, grads -- uncomment next comment grads={} grads['W1']=dW1 grads['W2']=dW2 grads['W3']=dW3 grads['b1']=db1 grads['b2']=db2 grads['b3']=db3 #return loss, grads
# update W1 += -step_size * dW1 b1 += -step_size * db1 W2 += -step_size * dW2 b2 += -step_size * db2 W3 += -step_size * dW3 b3 += -step_size * db3 # evaluate training set accuracy if NONLINEARITY == 'RELU': hidden_layer = relu(np.dot(X, W1) + b1) hidden_layer2 = relu(np.dot(hidden_layer, W2) + b2) elif NONLINEARITY == 'SIGM': hidden_layer = sigmoid(np.dot(X, W1) + b1) hidden_layer2 = sigmoid(np.dot(hidden_layer, W2) + b2) scores = np.dot(hidden_layer2, W3) + b3 predicted_class = np.argmax(scores, axis=1) print ('training accuracy: %.2f' % (np.mean(predicted_class == y))) #return cost, grads return plot_array_1, plot_array_2, W1, W2, W3, b1, b2, b3
#用sigmoid非线性训练网络 N = 100 # number of points per class D = 2 # dimensionality K = 3 # number of classes h=50 h2=50 # num_train_examples = X.shape[0] # # model={} # model['h'] = h # size of hidden layer 1 # model['h2']= h2# size of hidden layer 2 # model['W1']= 0.1 * np.random.randn(D,h) # model['b1'] = np.zeros((1,h)) # model['W2'] = 0.1 * np.random.randn(h,h2) # model['b2']= np.zeros((1,h2)) # model['W3'] = 0.1 * np.random.randn(h2,K) # model['b3'] = np.zeros((1,K)) # # (sigm_array_1, sigm_array_2, s_W1, s_W2,s_W3, s_b1, s_b2,s_b3) = three_layer_net('SIGM', X,y,model, step_size=1e-1, reg=1e-3)
#用ReLU非线性训练网络 #Re-initialize model, train relu net model={} model['h'] = h # size of hidden layer 1 model['h2']= h2# size of hidden layer 2 model['W1']= 0.1 * np.random.randn(D,h) model['b1'] = np.zeros((1,h)) model['W2'] = 0.1 * np.random.randn(h,h2) model['b2']= np.zeros((1,h2)) model['W3'] = 0.1 * np.random.randn(h2,K) model['b3'] = np.zeros((1,K))
(relu_array_1, relu_array_2, r_W1, r_W2,r_W3, r_b1, r_b2,r_b3) = three_layer_net('RELU', X,y,model, step_size=1e-1, reg=1e-3)
|