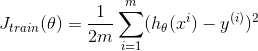机器学习5 正则化逻辑回归 和高偏差 高方差

part 1 数据导入以及可视化

fprintf("Loading and Visualizing Data....\n");
load('ex5data1.mat');
m=size(X,1);
plot(X,y,'rx','Markersize',10,'LineWidth',1.5);
xlabel("Change in Water level(x)");
ylabel("Water flowing out of the dam (y)");

part2 正则化逻辑回归损失函数

#对于2维向量，初始化的theta是和特征维数一样的
theta=[1;1];
J=linearRegCostFunction([one(m,1) X],y, theta,1);

定义函数linearRegCostFunction

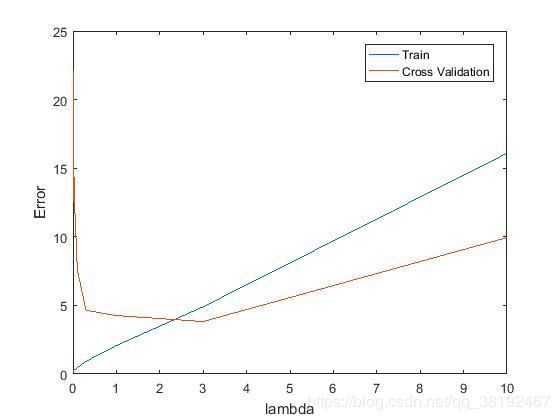
逻辑回归函数正则化的函数公式定义如下：

其中是正则化参数，帮助防止过拟合，正则化就是给损失函数一个惩罚；

function [J,grad]=linearRegCostFunction(X,Y,theta,lambda)
m=length(y);   #number of training examples
J=0;
grad=zeros[size(theta)]

theta_1=[0;theta(2:end)];
J=sum((X*theta-y).^2)/2*m+lambda/(2*m)*theta_1'*theta_1;
grad=(X'*(X*theta-y))/m+lamda/m*theta_1; 
end

part3 线性回归正则化梯度

求出当前梯度的值大小

theata=[1;1]

[J,grad]=linearRegCostFunction([ones(m,1) X],y ,theta,lambda);

part4 训练线性回归方程

#train linear regression with lambda=0
lambda=0;
[theta]=trainLinearReg([ones(m,1) X],y,lambda);
#画图如下
plot(X,y,'rx','MarkerSizer',10,'LineWithd',1.5);
xlabel("Change in water level (x)");
ylabel("Water flowing out of the dam (y)");
hold on ;
plot(X,[ones(m,1) X]*theta,'--','LineWitdh',2);
hold off;

function [theta]=trainLinearReg(X,y,lambda);
%Initialize the Theta
initial_theta=zeros(size(X,2),1);
%create 'short hand' for the cost function to minimized
costFunction=@(t) linearRegCostFunction(X,y,t,lambda);
%Now ,costFunction is a function that takes in only one argument
options=optimset('MaxIter',200,'GradObj','on');
%Minmize using fuming
theta=fmincg(costFunction,initial_theta,options);
end

最后得出训练出来的曲线，如下图：

从图可以看书这是一个高偏差的假设方程，一点都不够复杂来拟合我们都曲线，因此我们需要一个高方差的模型来拟合我们的训练数据。

在下一个部分我们会画出训练和测试的学习曲线来诊断我们的高偏差问题；

为了画出我们需要的学习曲线，我们需要训练和交叉验证集的误差在不同的训练样本下。为了获得不同的训练样本集合

我们采用下面的办法：X(1:i,:) and y(1:i)

你可以用trainLinearReg function 去寻找theta参数。需要格外注意的是，lambda 是不需要在学习曲线中，在学习得到了我们想要的参数 theta ，我们就应该计算训练误差和交叉验证集的误差，你应当使用下面的公式：

         

训练误差和交叉验证误差中是不需要包涵正则化！当你计算训练误差时，要确定在训练集合X(1:n,:) and y(1:n)

然而在交叉验证误差训练中，你应当计算在整个交叉验证集上面，你应该把计算好的errors 保存在error_train and error_val

function [error_train,error_val]=learningCurve(X,y,Xval,yval,lambda)
%需要注意的是Xval ,yval是整个交叉验证集的数据，在学习曲线中是始终不改变的
m=size(X,1); #number of training examples

error_train=zeros(m,1);
error_val=zeros(m,1);

for i=1:m
    theta=trainLinearReg(X(1:i,:),y(1:i),lambda);
    error_train(i)=linearRegCostFunction(X(1:i,:),y(1:i),theta,0);
    error_val(i)=linearRegCostFunction(Xval,yval,theta,0);
end
end
 

画出学习曲线图

lambda=0;
[error_train,error_val]=learningCure([oens(m,1) X],y,[ones(size(Xval,1)) Xval],yval,lambda);
plot(1:m,error_train,1:m,error_val);
title("Learning cure for linear regression");
legend("Train","Cross Validation");
xlabel("Number of training examples");
ylabel("Error")
axis([0 13 0 150]);

结论：你可以注意到训练误差和交叉验证误差都比较高随着训练样本的增多，这就是高偏差的问题。这个线性回归问题太简单了，不能够很好的去拟合我们的训练数据。下面我们会介绍多项式回归模型去更好的拟合我们的训练数据。

part5 特征映射和多项式回归

p = 8;

% Map X onto Polynomial Features and Normalize
X_poly = polyFeatures(X, p);
[X_poly, mu, sigma] = featureNormalize(X_poly);  % Normalize
X_poly = [ones(m, 1), X_poly];                   % Add Ones

% Map X_poly_test and normalize (using mu and sigma)
X_poly_test = polyFeatures(Xtest, p);
X_poly_test = bsxfun(@minus, X_poly_test, mu);
X_poly_test = bsxfun(@rdivide, X_poly_test, sigma);
X_poly_test = [ones(size(X_poly_test, 1), 1), X_poly_test];         % Add Ones

% Map X_poly_val and normalize (using mu and sigma)
X_poly_val = polyFeatures(Xval, p);
X_poly_val = bsxfun(@minus, X_poly_val, mu);
X_poly_val = bsxfun(@rdivide, X_poly_val, sigma);
X_poly_val = [ones(size(X_poly_val, 1), 1), X_poly_val]; 

part 6:学习曲线对多项式回归

lambda=0;
[theta]=trainLinearReg(X_poly,y,lambda);
figure(1)
plot(X,y,'rx','MarkerSize',10,'LineWidth',1.5);
plotFit(min(X,max(X),mu, sigma,theta,p);
xlabel("Change in water level (x)");
ylabel("Water flowing out of the dam (y)");
title("Polynomial Regression Fit (lambda=0)");

figure(2)
[error_train,error_val]=learningCurve(X_poly,y,X_poly_val,yval,lambda);
plot(1:m,error_train,1:m,error_val);
title("Polynomial Regression Learning Curve lambda=0");
xlabel("Number of training examples");
ylabel("Error");
axis([0 13 0 100]);
legend('Train','Cross Validation';)

不难看出这次曲线能够很好的拟合训练数据，并且在训练集上的误差很小，然而这也表明多项式回归模型出现了过拟合的问题

为了去更好的去理解lambda=0的情况，你可以看到，训练误差很小，但是在交叉验证集上误差却很大。它们两之间出现了一个很大间隔，说明了出现了高方差的问题，解决高方差的问题，你需要加入正则化到模型中，在下面的过程中，我们会选择不同的lambda去怎样历届正则化在模型中的作用。

我们分别画出lambda=1和lambda=100情况下，数据的拟合情况：

可以看出曲线比较合适的拟合我们的训练参数，既没有高偏差，也没出现高方差，出现一个很好的平衡在高偏差和高方差之间

下面来看一下学习曲线：

可以发现比lambda=0情况下，训练集误差与交叉验证集之间的误差间隔比较小，说明达到了你比较好的平衡。

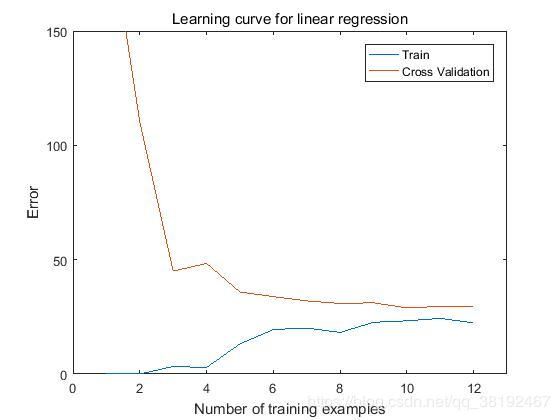
下面来看一下lambda=100情况下，拟合曲线与学习曲线是怎样的情况：

可以发现太大的lambda对训练数据拟合很不好，

下面我们会选取不同的lambda来拟合一个更好的模型；

[lambda_vec, error_train, error_val] = ...
    validationCurve(X_poly, y, X_poly_val, yval);

close all;
plot(lambda_vec, error_train, lambda_vec, error_val);
legend('Train', 'Cross Validation');
xlabel('lambda');
ylabel('Error');

function [lambda_vec, error_train, error_val] =validationCurve(X, y, Xval, yval)
lambda_vec = [0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]';
% You need to return these variables correctly.
error_train = zeros(length(lambda_vec), 1);
error_val = zeros(length(lambda_vec), 1);
for i = 1:length(lambda_vec)
      lambda = lambda_vec(i);
      theta = trainLinearReg(X, y,lambda);  % 用训练集训练出参数
      error_train(i) = linearRegCostFunction(X, y,theta,0);
      error_val(i) = linearRegCostFunction(Xval, yval,theta,0);           
end
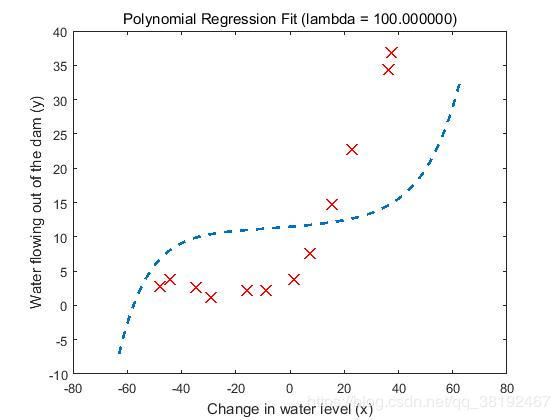
end

可以看出我们在lambda=3的情况下，可以发现训练误差和交叉验证误差之间的间隔比较小；

从而确定最好的lamba 参数就在3附近；