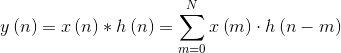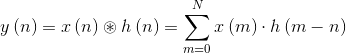目标跟踪整理（1）之MOSSE

之前读过一遍MOSSE了，读完还是有一种懵懵的感觉。最近还需要入基于相关滤波的目标跟踪的坑，所以又屁颠屁颠跑来深入理解一下，毕竟是相关滤波的始祖啊。

Visual Object Tracking using Adaptive Correlation Filter

 

一、补充知识：

１、复共轭：实部相等，虚部互为相反数（真的连这个都快记不清了。。。）

2、离散傅里叶变换（DFT），是傅里叶变换在时域和频域上都呈现离散的形式，将时域信号的采样变换为在离散时间傅里叶变换（DTFT）频域的采样。在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT，也应当将其看作经过周期延拓成为周期信号再作变换。在实际应用中通常采用快速傅里叶变换（FFT）以高效计算DFT。

二、卷积与相关：

１、卷积：

2、相关：

3、数学关系：

频域关系：

卷积：;  相关：

其中表示元素相乘，表示复共轭

４、物理关系：

卷积操作需要将其中一个信号进行反转，再平移、相乘再相加。而相关操作则不需要反转，相关是直接进行平移然后元素相乘再相加的。

三、基于相关滤波的跟踪器：

１、计算输入图像的２Ｄ傅里叶变换：

2、计算滤波器的２Ｄ傅里叶变换：

3.1 preprocessing

作者在这里说应用FFT算法会出现的一个问题是图像和滤波器被转化到一个环面的拓扑结构上，换句话说，图像的左边缘与右边缘被连接在了一起。上边缘和下边缘被连接到了一起，进行卷积操作时，图像在环形空间中旋转而不是像在空间域中一样。

是因为在做FFT之前需要现将图像和滤波器都进行周期性延拓

作者采用了三种方法来缓解这个现象所带来的问题：

１、采用对数函数将像素值进行里转换，据说是可以helps with low cintrast lighting situations

2、像素值归一化

３、加余弦窗

３.2　MOSSE filters

开始时需要一系列的训练图像和训练的输出，其中一般为峰值在目标中心的２ＤGaussian

训练一般是在傅里叶域进行的，有：

/   这里的除法为按元素除法

训练时的优化函数为：

   需要求解的为：

           (5)

作者观察了一下这个解，发现该解的分子为为输入与期望输出的乘积，而分母是输入的能量谱。而且从该公式可以看出ＵＭＡＣＥ这个跟踪器是MOSSE的一种特殊情况（没有看过UMACE不知道说的是啥意思），反正就是MOSSE更好。

3.3　与ASEF相比：

１、当训练样本只有一个时，求解的滤波器为精确滤波器，此时滤波器可从下式求解：

　　　（7）

但是只有一个训练样本容易过拟合，故：

２、ASEF采用平均的方法，即

但是它在小样本时特别是样本本身的频谱能量不高时表现不好(分母太小)，而此时ＭOSSE则更加稳定

３、其次针对样本本身的频谱能量不高的问题，作者认为可以采用正则化的方法缓解，即（5）式的分母更正为：

　　作者解释说这相当于在训练时候加了白噪声，使得滤波器更加稳定。

3.4　Filter initialization and online updates

１、训练集是在第一帧中采用随机放射变换产生了跟踪窗口的８个小绕动。

模型更新updates：

２、ASEF的更新策略为：

　　　　（9）

对该更新策略的理解：

加号后面一项比较好理解，把上一帧的滤波器以一定的权重加到该帧的滤波器中，加号前面的那一项可以结合（７）式去理解，即第一项是根据该帧求得的滤波器的解乘以权重

３、MOSSE的更新策略：

                                                            (10)

                    (11)

                    (12)

看完ASEF的更新策略再看MOSSE的更新策略有点懵圈：、都是怎么初始化的呢？根据第一帧（5）式的分子分母初始化？

这样分别更新分子分母，再相除得到更新后的滤波器与ASEF的更新相比优点在哪里呢？文章好像也没有再进行进一步的讨论，、初始化的问题留到阅读完代码吧。

3.5　failture detection and PSR

衡量峰值强度的一个简单方法为 peak to sidelobe ratio（PSR）峰值旁瓣比。计算相关输出g的PSR：根据峰值周围11×11的窗口分别计算峰值（即最大值）和剩下的像素的值。

其中是峰值，和是旁瓣的均值和标准差。

PSR:20-60时峰值较稳定，7左右时跟踪失败或者已经发生遮挡

遗留问题：Ａi和Ｂi的初始化、PSR计算方法、附录Ａ的推导也还没搞懂。。。