02-线性结构2 一元多项式的乘法与加法运算-中国大学MOOC-陈越、何钦铭-数据结构-2017秋

题目介绍

设计函数分别求两个一元多项式的乘积与和。

输入格式:

输入分2行，每行分别先给出多项式非零项的个数，再以指数递降方式输入一个多项式非零项系数和指数（绝对值均为不超过1000的整数）。数字间以空格分隔。

输出格式:

输出分2行，分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。数字间以空格分隔，但结尾不能有多余空格。零多项式应输出0 0。

---

输入样例

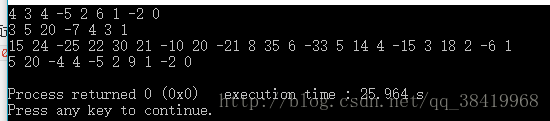
4 3 4 -5 2  6 1  -2 0
3 5 20  -7 4  3 1

输出样例

15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0

---

我的代码如下：

#include <stdio.h>
#include <stdlib.h>


typedef struct PolyNode *Polynomial;
struct PolyNode{
    int coef;
    int expon;
    Polynomial link;
};
Polynomial ReadPoly();
Polynomial Add(Polynomial P1,Polynomial P2);
Polynomial Mult(Polynomial P1,Polynomial P2);
void PrintPoly(Polynomial P);
void Attach(int c,int e,Polynomial *pRear);
int main()
{
    Polynomial P1,P2,PP,PS;
    P1 = ReadPoly();
    P2 = ReadPoly();
    PP = Mult(P1,P2);
    PrintPoly(PP);
    PS = Add(P1,P2);
    PrintPoly(PS);

    return 0;
}

Polynomial ReadPoly()
{
    Polynomial p,Rear,t;
    int N,c,e;
    scanf("%d",&N);
//    链表头空结点
    p = (Polynomial)malloc(sizeof(struct PolyNode));
    p->link = NULL;
    Rear = p;
    while(N--)
    {
        scanf("%d %d",&c,&e);
        if(abs(c) <= 1000 && abs(e) <= 1000)
            Attach(c,e,&Rear);
    }
//    删除临时生成的头结点
    t = p;
    p = p->link;
    free(t);
    return p;
}

Polynomial Add(Polynomial P1,Polynomial P2)
{
    Polynomial p1,p2,P,p,t;
    int sum;
    p1 = P1;
    p2 = P2;
    P = (Polynomial)malloc(sizeof(struct PolyNode));
    P->link = NULL;
    p = P;
    while(1)
    {
        if(p1 != NULL&&p2 != NULL)
        {
            if(p1->expon == p2->expon)
            {
                sum = p1->coef + p2->coef;
                if(sum != 0)
                Attach(sum,p1->expon,&p);
                p1 = p1->link;
                p2 = p2->link;

            }
            else if(p1->expon > p2->expon)
            {
                Attach(p1->coef,p1->expon,&p);
                p1 = p1->link;
            }
            else
            {
                Attach(p2->coef,p2->expon,&p);
                p2 = p2->link;
            }
        }
        else if(p1 != NULL)
        {
            Attach(p1->coef,p1->expon,&p);
            p1 = p1->link;
        }
        else if(p2 != NULL)
        {
            Attach(p2->coef,p2->expon,&p);
            p2 = p2->link;
        }
        else
            break;
    }
    p->link = NULL;
    t = P;
    P = P->link;
    free(t);
    return P;
}

Polynomial Mult(Polynomial P1,Polynomial P2)
{
    Polynomial p1,p2,P,p,t,t1;
    int c,e;
    p1 = P1;
    p2 = P2;
    P = (Polynomial)malloc(sizeof(struct PolyNode));
    P->link = NULL;
    p = P;
    if(P1 == NULL || P2 == NULL)
        return NULL;
    while(p2 != NULL)
    {
        Attach(p1->coef*p2->coef,p1->expon+p2->expon,&p);
        p2 = p2->link;
    }
    p1 = p1->link;
    while( p1 != NULL)
    {
        p2 = P2;
        p = P;
        while(p2 != NULL)
        {
            c = p1->coef * p2->coef;
            e = p1->expon + p2->expon;
            while(p->link != NULL && p->link->expon > e)
                p = p->link;
            if(p->link != NULL && p->link->expon == e)
            {
                if((p->link->coef + c) != 0)
                {
                    p->link->coef += c;
                }
                else
                {
                    t = p->link;
                    p->link = t->link;
                    free(t);
                }
            }
            else
            {
                t = (Polynomial)malloc(sizeof(struct PolyNode));
                t->coef = c;
                t->expon = e;
                t->link = p->link;
                p->link = t;
                p = p->link;
            }
            p2 = p2->link;
        }
        p1 = p1->link;
    }
    t1 = P;
    P = P->link;
    free(t1);
    return P;
}

void PrintPoly(Polynomial P)
{
    int flag = 0;
    if(P == NULL)
    {
        printf("0 0\n");
        return ;
    }
    while(P != NULL)
    {
        if(!flag)
            flag = 1;
        else
            printf(" ");
        printf("%d %d",P->coef,P->expon);
        P = P->link;
    }
    printf("\n");
}
void Attach(int c,int e,Polynomial *pRear)
{
    Polynomial p;
    p = (Polynomial)malloc(sizeof(struct PolyNode));
    p->coef = c;
    p->expon = e;
    p->link = NULL;
    (*pRear)->link = p;
    *pRear = p;

}

---

运行结果：

在PAT中运行结果：

---

结论：
认真看mooc上的视频跟代码，一般情况下都能编出来。