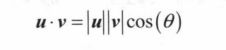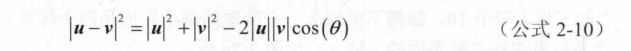深度学习和计算机视觉中的基础数学知识（一）
2.1 线性变换与非线性变换
2-1叫相加性，2-2叫齐性
2.1.2 旋转、缩放与矩阵乘法
旋转坐标
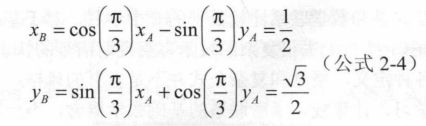
矩阵形式
缩放坐标的矩阵形式（B → \to →C）
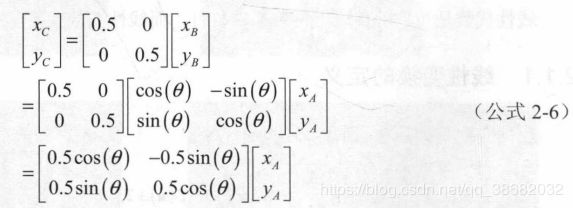
2.1.3 点积和投影
点积定义： 两个向量对应元素两两相乘，并求和
从矩阵角度看，相当于 u v T u v^T uvT， u 乘 v 的 转 置 u乘v的转置 u乘v的转置
（内积是点积的推广，点积是欧几里得空间的标准内积）
-
向量长度的运算
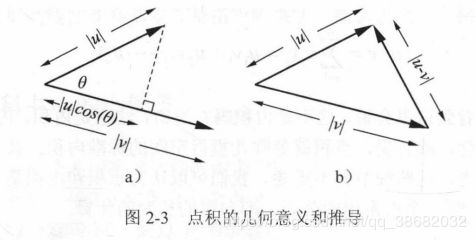
投影 ：一个向量在另一个向量方向上的分量的长度
点积的几何意义：一个向量在另一个向量方向的投影的长度与另一个向量的长度相乘（比如图中， 2 × 3 = 6 2\times 3=6 2×3=6） -
投影长度的计算
具有交换性，（可以u投v ✖ v，也可以 v 投 u✖u，不影响结果） -
余弦相似度的推导
在机器学习中经常用到。
2.1.4 矩阵乘法的几何意义(1)
1.从投影的角度理解
矩阵 T ∈ R m × n \boldsymbol T \in \mathbb R^{m\times n} T∈Rm×n,乘以向量 ( x 1 , x 2 , . . . , x n ) (x_1,x_2,...,x_n) (x1,x2,...,xn)
分解为 矩阵的每一行向量 与 待乘向量 点积结果 形成新向量
等于 x x x 在 a i , ∗ a_{i,*} ai,∗上的投影
如果a看成一个坐标轴的单位向量，那么x在a上的投影就是，x在坐标轴上投影的长度
(因为a是单位向量（长度为1），所以投影长度乘1长度没有变。）
乘法的最终结果，是x在以每个a为坐标轴单位向量的新坐标系下的坐标。
-举前面的例子（旋转缩放中，）
变换后的坐标轴的单位向量。
图左： 向量在新坐标系（虚线）的投影。
图右：新坐标系取代老坐标系，得到新的坐标。
2.坐标映射角度理解
坐标系的轴不正交，甚至向量长度不为1，就难以想象矩阵乘法的结果。
（正交在本节的解释：任意坐标轴方向上的向量，在其他坐标轴方向上的投影长度都是0）
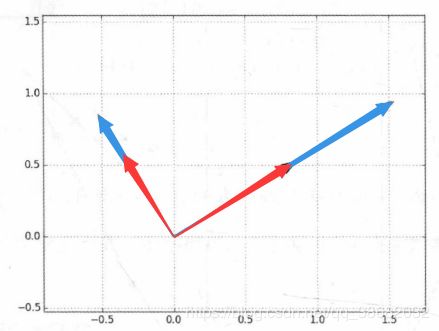
比如下面这个例子。
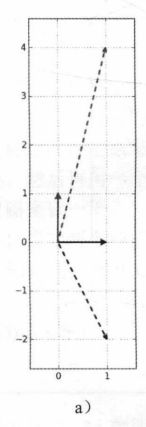
a）中（1，1）在两个行向量（1，4）和（2，-1）上的投影还能理解
b）第一眼看不出来什么东西 （至少博主没看出来），因为参考坐标系变换了，而平时人们想象的都是笛卡尔坐标系。
笛卡尔坐标系（Cartesian coordinates）就是直角坐标系和斜坐标系的统称。
相交于原点的两条数轴，构成了平面放射坐标系。如两条数轴上的度量单位相等，则称此放射坐标系为笛卡尔坐标系。两条数轴互相垂直的笛卡尔坐标系，称为笛卡尔直角坐标系，否则称为笛卡尔斜角坐标系。
我们先研究一下，坐标轴单位向量的变化（1，0），（0，1）与旋转矩阵相乘之后
结论：第i维度的单位向量，在矩阵乘法变换之后，就是第i列向量
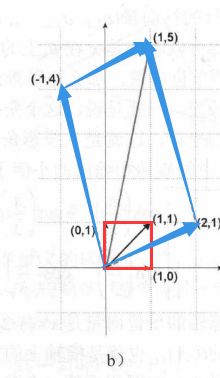
原来的红色矩形被拉伸成蓝色的平行四边形了，也就得到了(1,1)变换后的结果(1,5)
重新看投影角度的例子。（蓝色，新的坐标轴单位向量，红色是老的坐标轴单位向量）
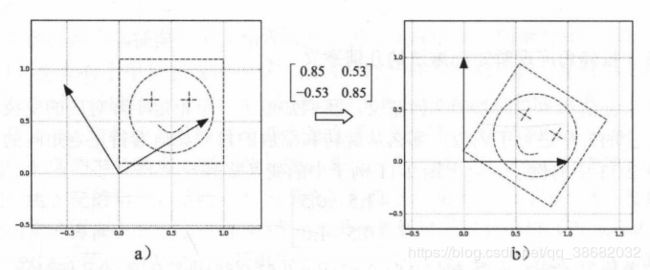
都是例子（在矩形里加了一个笑脸，更加直观）
矩阵相加，实现平移
上图如果是一个回归问题，矩阵乘法不能单独解决问题，必须加上一个矩阵，成为偏置（bias）
y = A x + b \boldsymbol{y=Ax+b} y=Ax+b,就叫做仿射变换，（就是一个线性变换加一个平移变换）
2.1.5 本征向量和本征值 (特征向量，特征值）
本征向量在变换后，方向没有改变。（或者相反, λ < 0 \lambda<0 λ<0）
- 例子
单位坐标轴的变换
上个例子是非对称矩阵，机器学习中常用的是对称矩阵，尤其是其中的正定矩阵。
正定矩阵定义：（x 为任意非0 向量， A 对称矩阵）
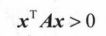
向量与正定矩阵相乘后的变换结果不会 到与自身垂直平面的另一侧（夹角不超过90度）。
对称矩阵：元素以主对角线为对称轴对应相等的矩阵。
两个特征向量相互垂直。
红色变换前，蓝色变换后。
如果在原坐标系画单位长度为半径的圆，在变换后就变成了椭圆。
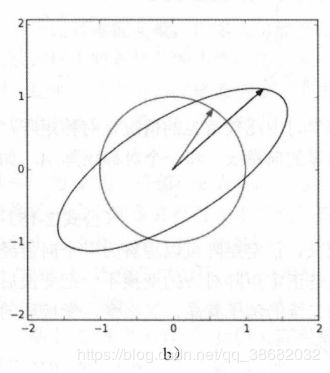
特征值和特征向量刚好是椭圆长短轴的一半长度和方向 （PCA的底层思想）
矩阵变化的前后可以在空间里找到一组正交的向量，在变换前后方向不变，空间只是在这组方向上进行伸缩。
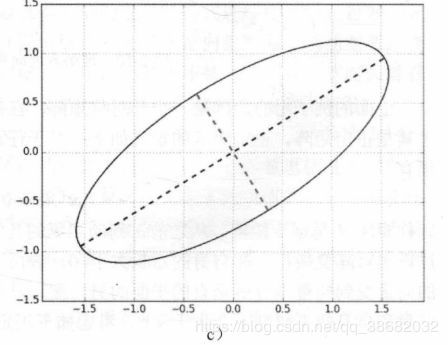
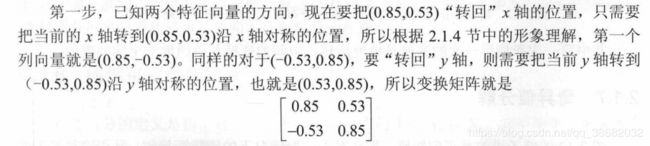
2.1.6 矩阵乘法的几何意义（2）
- 从旋转和拉伸的角度理解
变换矩阵：
接下来把 变换分解为3个步骤
第一次变换，把两个特征向量作为的新的单位坐标轴向量。
第二次变换，沿着轴进行缩放。
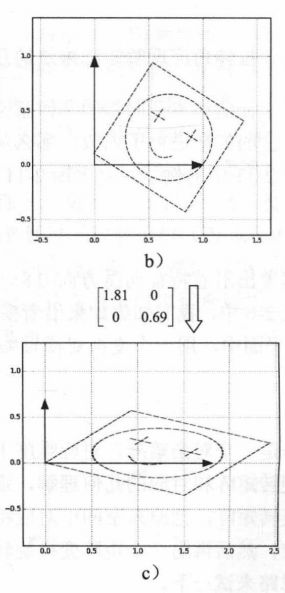
第三步，把坐标轴转回原来的位置（乘以一个转置）。
下图为三步整体图。
2.1.7 奇异值分解
（把上节正定矩阵分解的例子推广到一般情况）
∑ \sum ∑表示一个对角矩阵。 U , V U,V U,V为正交矩阵。
2.1.8 线性可分性和维度
2.1.9 非线性变换
