正则化公式以及L1正则化产生稀疏阵的原因

• 范数的公式

范数是衡量某个向量空间（或矩阵）中的每个向量以长度或大小。范数的一般化定义：对实数p>=1， 范数定义如下：

L1范数
当p=1时，是L1范数，其表示某个向量中所有元素绝对值的和。
L2范数
当p=2时，是L2范数， 表示某个向量中所有元素平方和再开根， 也就是欧几里得距离公式。

• 实际应用与选择

下面以sklearn里逻辑回归算法为例，具体看下两者的不同

创建逻辑回归模型时，有个参数 penalty ，其取值有‘l1’或‘l2’，实际上就是指定前面介绍的正则项的形式。

L1 范数是指向量中各个元素绝对值之和，也叫“稀疏规则算子”（Lasso regularization）。范数作为正则项，会让模型参数θ稀疏化， 既让模型参数向量里为0的元素尽量多。在支持向量机（support vector machine）学习过程中，实际是一种对于成本函数(cost function)求解最优，得出稀疏解。

L2 范数作为正则项式让模型参数尽量小，但不会为0，尽量让每个特征对预测值都有一些小的贡献，得出稠密解。
在梯度下降算法的迭代过程中，实际上是在成本函数的等高线上跳跃，并最终收敛在误差最小的点上（此处为未加正则项之前的成本误差）。而正则项的本质就是惩罚。 模型在训练的过程中，如果没有遵守正则项所表达的规则，那么成本会变大，即受到了惩罚，从而往正则项所表达的规则处收敛。 成本函数在这两项规则的综合作用下，正则化后的模型参数应该收敛在误差等值线与正则项等值线相切的点上。

作为推论， L1 范数作为正则项由以下几个用途：

• 特征选择： 它会让模型参数向量里的元素为0的点尽量多。 因此可以排除掉那些对预测值没有什么影响的特征，从而简化问题。所以 L1 范数解决过拟合措施实际上是减少特征数量。
• 可解释性： 模型参数向量稀疏化后，只会留下那些对预测值有重要影响的特征。 这样我们就容易解释模型的因果关系。 比如针对某个癌症的筛查，如果有100个特征，那么我们无从解释到底哪些特征对阳性成关键作用。 稀疏化后，只留下几个关键特征，就更容易看到因果关系

由此可见， L1 范数作为正则项，更多的是一个分析工具，而适合用来对模型求解。因为它会把不重要的特征直接去除。 大部分情况下，我们解决过拟合问题，还是选择 L2 单数作为正则项， 这也是 sklearn 里的默认值。

• L1正则化会产生稀疏阵的原因

上面提到,L1会让模型参数θ稀疏化，为什么会有这种效果，可以参考下面两种解释。

首先看下稀疏阵的定义：

对于一个矩阵而言，若数值为零的元素远远多于非零元素的个数，且非零元素分布没有规律时，这样的矩阵被称作稀疏矩阵；与之相反，若非零元素数目占据绝大多数时，这样的矩阵被称作稠密矩阵。

稀疏矩阵在工程应用中经常被使用，尤其是在通信编码和机器学习中。若编码矩阵或特征表达矩阵是稀疏矩阵时，其计算速度会大大提升。对于机器学习而言，稀疏矩阵应用非常广，比如在数据特征表示、自然语言处理等领域。

L1正则化导致稀疏阵产生的两种解释

第一种解释：

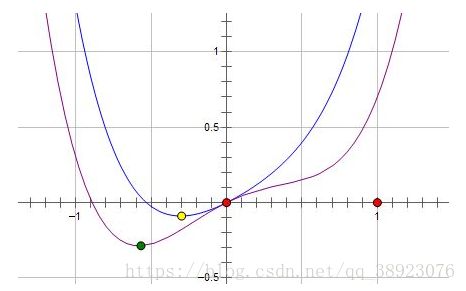
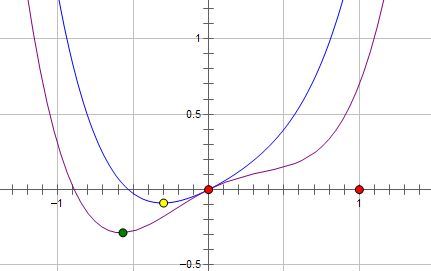
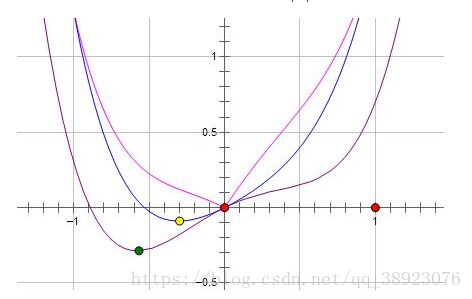
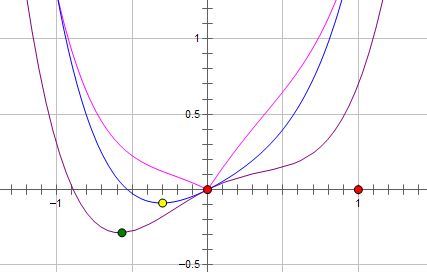
假设费用函数 L 与某个参数 x 的关系如图所示：

 

则最优的 x 在绿点处，x 非零。

现在施加 L2 regularization，新的费用函数（）如图中蓝线所示：

最优的 x 在黄点处，x 的绝对值减小了，但依然非零。

而如果施加 L1 regularization，则新的费用函数（）如图中粉线所示：

最优的 x 就变成了 0。这里利用的就是绝对值函数的尖峰。

两种 regularization 能不能把最优的 x 变成 0，取决于原先的费用函数在 0 点处的导数。
如果本来导数不为 0，那么施加 L2 regularization 后导数依然不为 0，最优的 x 也不会变成 0。
而施加 L1 regularization 时，只要 regularization 项的系数 C 大于原先费用函数在 0 点处的导数的绝对值，x = 0 就会变成一个极小值点。

上面只分析了一个参数 x。事实上 L1 regularization 会使得许多参数的最优值变成 0，这样模型就稀疏了。

 

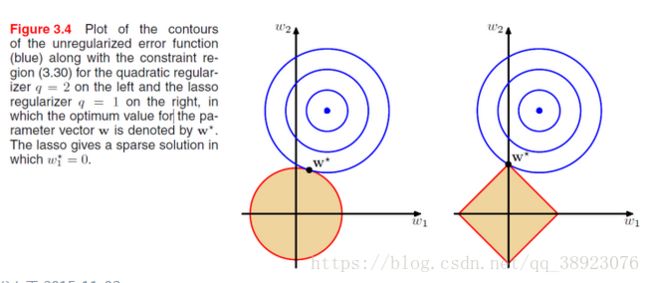
第二种解释

目标是把  的解限制在黄色区域内，同时使得经验损失尽可能小。

参考链接：https://www.zhihu.com/question/37096933/answer/70426653

                  http://ihoge.cn/2018/Logistic-regression.html