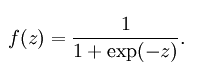基于Tensorflow框架-------深度学习实战(一)LeNet模型完全解析

本文适合理论和原理都了解的学者，当然对于小白也可以共同学习，只不过无法讲的那么详细。机器学习届的"Hello World"就是MNIST数据集，因为笔者的电脑原因，配置不高，所有打算用MNIST作为模型框架的敲门砖。

首先用卷积神经网络训练MNIST数据集，我们这里直接上经典的模型LeNet结构。

 

 

这是LeNet模型的基本结构，现在进行分解：

首先导入数据，这里使用的是MNIST数据集，对数据的导入使用给定的数据导入方法以及相关的包，代码如下：

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import time

紧接着声明输入图片的数据和类别：

注意：mnist数据集里面的图片的大小是28*28，原图模型里面的是32*32，所以我们需要根据我们实际的数据集进行写模型。

x=tf.placeholder('float',[None,784])
y_=tf.placeholder('float',[None,10])

注意：有些人可能不明白这里的784是什么意思，首先一张mnist图片是28*28的，那么784个字节代表了一张图片的所有信息，而我们这里是将784变成一行向量，则代表一行是一张图片。

这里的MNIST数据集是以[None,784]的数据格式存放的，而对于卷积神经网络来说，需要把图像的位置信息进行保存，因此这里将一维的数组重新转换为二维图像数组矩阵:

x_image=tf.reshape(x,[-1,28,28,1])

这里表示的是将一行的图片数据展开，形成28*28*1的三维矩阵。

根据LeNet的模型可以看到

第一层C1：滤波器个数为6，滤波器大小为5*5，单通道，偏执值为6个，进行卷积时步长为1且填充。实现如下：

filter1 = tf.Variable(tf.truncated_normal([5,5,1,6]))
bias1 = tf.Variable(tf.truncated_normal([6]))
conv1 = tf.nn.conv2d(x_image,filter1,strides=[1,1,1,1],padding='SAME')
h_conv1 = tf.nn.sigmoid(conv1+bias1)

这里的具体意思我就不说了，因为大家原理都清楚，我就简单的说一下，这里filter1定义的是6个5*5*1的三维随机数组，偏置值也是6个。最后通过sigmoid函数求得第一个卷积层输出结果。

第一层的运算后，其变化为：

C1
输入大小：28*28
核大小：5*5
核数目：6
输出大小：28*28*6
训练参数数目：(5*5+1)*6=156
连接数：(5*5+1)*6*(32-2-2)*(32-2-2)=122304

 

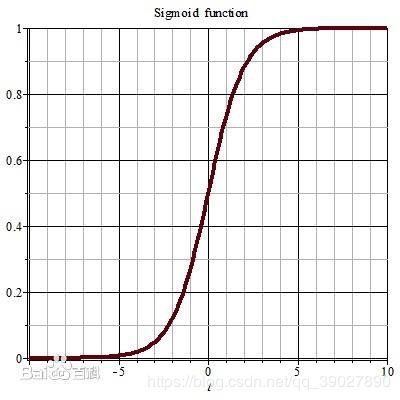
这里补充一下关于sigmoid激活函数的印象，看下数学公式大家应该能想起来：

第二层S2是在第一层卷积层之后的一个池化层，这里使用的是maxPooling，对于2*2大小的框进行最大特征取值。

maxPool2=tf.nn.max_pool(h_conv1,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

这是定义了一个2*2大小，步长为2，填充的池化层，经过这层运算后，图片的大小变为

S2
输入大小：28*28*6
核大小：2*2
核数目：1
输出大小：14*14*6
训练参数数目：2*6=12，2=(w,b)
连接数：(2*2+1)*1*14*14*6 = 5880

第三层C3:依旧是卷积层，滤波器大小为5*5，6个通道，个数为16，偏执值也为16，卷积时的步长为1且不填充。其后的池化层将特征进行再一次压缩，代码如下：

filter2 = tf.Variable(tf.truncated_normal([5,5,6,16]))
bias2 = tf.Variable(tf.truncated_normal([16]))
conv2 = tf.nn.conv2d(maxPool2,filter2,strides=[1,1,1,1],padding='VALID')
h_conv2 = tf.nn.sigmoid(conv2+bias2)

C3
输入大小：14*14*6
核大小：5*5
核数目：16
输出大小：10*10*16
训练参数数目：6*(3*5*5+1) + 6*(4*5*5+1) + 3*(4*5*5+1) + 1*(6*5*5+1)=1516
连接数：(6*(3*5*5+1) + 6*(4*5*5+1) + 3*(4*5*5+1) + 1*(6*5*5+1))*10*10=151600

 

第四层S4:池化器大小为2*2，步长为2，填充，代码如下：

maxPool3 = tf.nn.max_pool(h_conv2,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

S4
输入大小：10*10*16
核大小：2*2
核数目：1
输出大小：5*5*16
训练参数数目：2*16=32
连接数：(2*2+1)*1*5*5*16=2000

 

第五层C5：也是卷积层，滤波器的大小为5*5，16个通道数，个数为120个，偏置值为120，运行卷积的步长为1，不填充，代码如下：

filter3 = tf.Variable(tf.truncated_normal([5,5,16,120]))
bias3 = tf.Variable(tf.truncated_normal([120]))
conv3 = tf.nn.conv2d(maxPool3,filter3,strides=[1,1,1,1],padding='VALID')
h_conv3 = tf.nn.sigmoid(conv3+bias3)

C5
输入大小：5*5*16
核大小：5*5
核数目：120
输出大小：120*1*1
训练参数数目：(5*5*16+1)*120*1*1=48120（因为是全连接）
连接数：(5*5*16+1)*120*1*1=48120

第六层F6：全连接层，全连接层的作用在整个卷积神经网络中起到“分类器”的作用。如果说卷积层，池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的“分布式特征表达”映射到样本标记空间的作用。全连接层的滤波器大小为7*7，120个通道，个数为80。偏置值为80个。

代码如下：

#全连接层
#权值参数
W_fc1 = tf.Variable(tf.truncated_normal([1*1*120*80]))
#偏置值
b_fc1 = Varibale(tf.truncated_normal([80]))
#将卷积的输出展开
h_pool2_flat = tf.reshape(h_conv3,[-1,1*1*120])
#神经网络计算，并添加sigmoid函数
h_fc1 = tf.nn.sigmoid(tf.matmul(h_pool2_flat,W_fc1)+b_fc1)

F6
输入大小：120
输出大小：84
训练参数数目：(120+1)*84=10164
连接数：(120+1)*84=10164

 

最后一层输出层F7：最后一层的道理相比大家都知道，这里对全连接后的数据进行重新展开，将二维数据重新展开成一维数组之后计算每一行的元素个数。最后一个输出层在使用了softmax进行概率的计算。代码如下：

#输出层，使用softmax函数进行多分类
W_fc2 = tf.Variable(tf.truncated_normal([80,10]))
b_fc2 = tf.Variable(tf.truncated_normal([10]))
y_conv = tf.nn.softmax(tf.matmul(h_fc1,W_fc2)+b_fc2)

 

F7

输入大小：84

输出大小为：10

训练参数数目：(84+1)*10=850

连接数：(84+1)*10=850

最后是交叉熵作为损失函数，使用梯度下降算法(学习率是0.001)来对模型进行训练。代码如下：

cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
#使用GDO优化算法来调参
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(cross_entropy)

以上就是完整的模型解析，下面贴出相应的完整的代码：

#-*-coding:utf-8-*-
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import time

x=tf.placeholder('float',[None,784])
y_=tf.placeholder('float',[None,10])

x_image=tf.reshape(x,[-1,28,28,1])

#C1:第一层卷积层，初始化卷积核参数，偏执值，该卷积层5*5大小，一个通道，共有6个不同卷积核
filter1 = tf.Variable(tf.truncated_normal([5,5,1,6]))
bias1 = tf.Variable(tf.truncated_normal([6]))
conv1 = tf.nn.conv2d(x_image,filter1,strides=[1,1,1,1],padding='SAME')
h_conv1 = tf.nn.sigmoid(conv1+bias1)

#S2
maxPool2=tf.nn.max_pool(h_conv1,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

#C3:
filter2 = tf.Variable(tf.truncated_normal([5,5,6,16]))
bias2 = tf.Variable(tf.truncated_normal([16]))
conv2 = tf.nn.conv2d(maxPool2,filter2,strides=[1,1,1,1],padding='VALID')
h_conv2 = tf.nn.sigmoid(conv2+bias2)

#S4
maxPool3 = tf.nn.max_pool(h_conv2,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

#C5
filter3 = tf.Variable(tf.truncated_normal([5,5,16,120]))
bias3 = tf.Variable(tf.truncated_normal([120]))
conv3 = tf.nn.conv2d(maxPool3,filter3,strides=[1,1,1,1],padding='VALID')
h_conv3 = tf.nn.sigmoid(conv3+bias3)


#全连接层
#权值参数
W_fc1 = tf.Variable(tf.truncated_normal([1*1*120,80]))
#偏置值
b_fc1 = tf.Variable(tf.truncated_normal([80]))
#将卷积的输出展开
h_pool2_flat = tf.reshape(h_conv3,[-1,1*1*120])
#神经网络计算，并添加sigmoid函数
h_fc1 = tf.nn.sigmoid(tf.matmul(h_pool2_flat,W_fc1)+b_fc1)

#输出层，使用softmax函数进行多分类
W_fc2 = tf.Variable(tf.truncated_normal([80,10]))
b_fc2 = tf.Variable(tf.truncated_normal([10]))
y_conv = tf.nn.softmax(tf.matmul(h_fc1,W_fc2)+b_fc2)

cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
#使用GDO优化算法来调参
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(cross_entropy)
sess = tf.InteractiveSession()

#测试正确率
correct_prediction =  tf.equal(tf.argmax(y_conv,1),tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction,"float"))

#所有变量进行初始化
sess.run(tf.initialize_all_variables())

#获取mnist数据
mnist_data_set = input_data.read_data_sets('mnist_data',one_hot=True)

#进行训练
start_time = time.time()
for i in range(20000):
    #获取训练数据
    batch_xs, batch_ys = mnist_data_set.train.next_batch(200)

    #每迭代100个batch,对当前训练数据进行测试，输出当前预测准确率
    if i%2 == 0:
        train_accuray = accuracy.eval(feed_dict={x:batch_xs,y_:batch_ys})
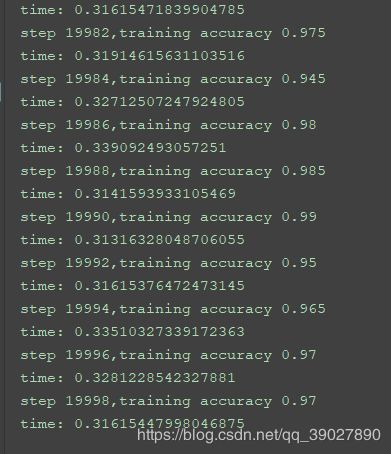
        print("step %d,training accuracy %g"%(i,train_accuray))
        #计算间隔时间
        end_time = time.time()
        print('time:',(end_time-start_time))
        start_time = end_time
    #训练数据
    train_step.run(feed_dict={x:batch_xs,y_:batch_ys})

#关闭会话
sess.close()

经过20000次的训练后，在训练集上的准确率为0.99：

以上这是最粗鲁的代码写法，这么写的目的只是为了让大家更好的理解，接下来我们要进行程序的重构--模块化设计

首先使用ReLU激活函数代替sigmoid函数，从数学的上看，非线性的sigmoid函数对中央区的信号增益较大，对两侧区的信号增益较小，在信号的特征空间映射上，有很好的效果。但是由于sigmoid函左右两端在很大程度上接近极值，容易饱和，因此在进行计算时当传递的数值过小或者过大时会使得神经元梯度接近于0，这使得在模型计算时会多次计算接近于0的梯度，从而导致花费了学习时间却使得权重没有更新。

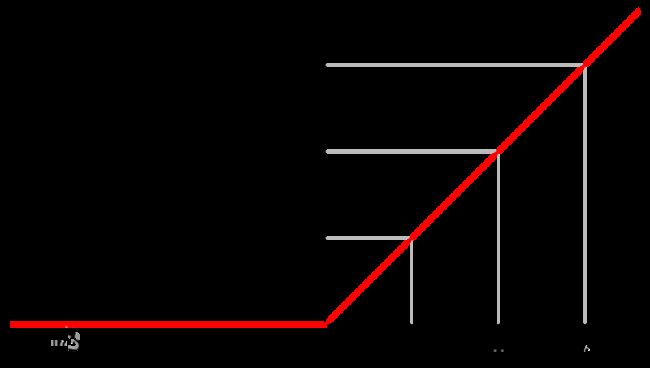
为了克服sigmoid函数容易产生提取梯度迟缓这一弊端，导出了一种新的激活函数ReLU函数，函数如图：

 

ReLU主要有以下几个优点：

收敛快：对于SGD的收敛有巨大的加速作用，可以看到对于达到阈值的数据其激活力度是随数值的加大而增大，且呈现一个线性关系。

计算简单：ReLU的算法较为简单，单纯一个值的输入输出不需要进行一系列的复杂计算，从而获得激活值。

不易过拟合：使用ReLU进行模型计算时，一部分神经元在计算时如果有一个过大的梯度经过，则次神经元的梯度会被强行设置为0，而在整个其后的训练过程中这个神经元都不会被激活，这会导致数据多样化的丢失，但是也能防止过拟合。

下面开始正式的代码优化

首先可以看到，为了模型的正常使用，在图计算过程中需要使用大量的权重值和偏置量。这些都是由Tensorflow变量所设置。而变量带来的问题就是在每次图对话计算过程中都要被反复初始化和赋予新值，因此在程序的编写过程中为了更好地反应模型的设计问题，不在Tensorflow进行初始化运算时反复进行格式化。

def weight_variable(shape):
    initial = tf.truncated_normal(shape,stddev=0.1)
    return tf.Variable(initial)

#初始化单个卷积核上的偏置值
def bias_variable(shape):
    initial = tf.constant(0.1,shape=shape)
    return tf.Variable(initial)

#输入特征x，用卷积核W进行卷积运算，strides为卷积核移动步长，
def conv2d(x,w,padding):
    return tf.nn.conv2d(x,w,strides=[1,1,1,1],padding=padding)

#对x进行最大池化操作，ksize进行池化的范围
def max_pool_2x2(x):
    return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

这步的完整代码，我就不提供了，希望读者能自行完成，毕竟多动手才是王道。

 

下面补充一下关于模型保存的办法，不然训练后得到的只有数据的准确率，好不容易等出来的权值和偏置值都消失了。

# 之前是各种构建模型graph的操作(矩阵相乘，sigmoid等等....)

saver = tf.train.Saver() # 生成saver

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer()) # 先对模型初始化

    # 然后将数据丢入模型进行训练blablabla

    # 训练完以后，使用saver.save 来保存
    saver.save(sess, "save_path/file_name") #file_name如果不存在的话，会自动创建

 

然后就是模型的载入：

saver = tf.train.Saver()

with tf.Session() as sess:
    #参数可以进行初始化，也可不进行初始化。即使初始化了，初始化的值也会被restore的值给覆盖
    sess.run(tf.global_variables_initializer())     
    saver.restore(sess, "save_path/file_name") #会将已经保存的变量值resotre到 变量中。

简单的说就是通过saver.save来保存模型，通过saver.restore来加载模型