2013年阿里巴巴暑期实习生招聘试题及答案
如有问题,请留言
答题说明:
1.答题时间90分钟,请注意把握时间;
2.试题分为四个部分:单项选择题(10题,20分)、不定向选择题(4题,20分)、填空问答(5题,40分)、综合体(1题,20分);
3.考试说明。
一、单项选择题
1.下列说法不正确的是:
A. SATA硬盘的读取速度大约为500Mbps/s
B. 读取18XDVD光盘数据的速度为1Gbps
C. 千兆以太网的数据读取速度为1Gpbs
D. 读取DDR3内存数据的速度为100Gbps
感觉这道题如果自己碰上的话只能排除法了。首先要知道Gbps的含义:即 1G bit per second;
首先C肯定是对的,千兆=1000百万=10^9=1G;
对于A. SATA硬盘即使用(SerialATA)口的硬盘又叫串口硬盘,读取速率:
| 版本 |
带宽 |
速度 |
数据线最大长度 |
| SATA 3.0 |
6Gb/s |
600MB/s |
2米 |
| SATA 2.0 |
3Gb/s |
300MB/s |
1.5米 |
| SATA 1.0 |
1.5Gb/s |
150MB/s |
1米 |
| PATA |
1Gb/s |
133MB/s |
0.5米 |
所以A 也是对的。
对于B,网上给出1XDVD的速率为1350KB/s18X=1350*18*1024*8=2.0*10^8=0.2Gpbs.发现和选项有些偏差。
对于D,网上给出的是1.6Gbps.所以选 D
2.()不能用于Linux中的进程通信
A.共享内存 B.命名管道 C.信号量 D.临界区
D.Linux进程间进行通信可以通过以下几个方法:管道(命名管道);共享内存;信号量;消息队列;套接字;
3.设在内存中有P1,P2,P3三道程序,并按照P1,P2,P3的优先级次序运行,其中内部计算和IO操作时间由下表给出(CPU计算和IO资源都只能同时由一个程序占用):
P1:计算60ms---》IO 80ms---》计算20ms
P2:计算120ms---》IO 40ms---》计算40ms
P3:计算40ms---》IO 80ms---》计算40ms
并行完成三道程序比单道运行节省的时间是()
A.80ms B.120ms C.160ms D.200ms
这里节约的时间是在一个进程进行cpu操作的时候另一个进程可以进行io操作,反之也是可以的。但是要注意的是,高优先级的进程可以剥夺资源并直至完成才让出资源。
本题,在p1进行io80ms期间,p2可占用cpu80ms,之后被迫让出给p1执行cpu20ms后继续完成还剩的cpu40ms。按照这种思路,共可以节约80+40+40=160ms.选C ;
4.两个等价线程并发的执行下列程序,a为全局变量,初始为0,假设printf、++、--操作都是原子性的,则输出不肯哪个是()
void foo() {
if(a <= 0) {
a++;
}
else {
a--;
}
printf("%d", a);
}A.0 1 B.1 0 C.1 2 D.2 2
这里考了原子性的操作,即不可被中断的操作。0 1输出肯定是不可以的,最多是 0 0。因为假如p1先取得a=0;肯定+1;之后p2取得a=1,a-1得a=0;之后 p1 print这个0,那么p2print的也是这个0;选A。
5.给定fun函数如下,那么fun(10)的输出结果是()
int fun(int x) {
return (x==1) ? 1 : (x + fun(x-1));
}A.0 B.10 C.55 D.3628800
考的是递归,挺简单的:1+2+…+10=55;
6.在c++程序中,如果一个整型变量频繁使用,最好将他定义为()
A.auto B.externC.staticD.register
D. 如果一个变量被频繁使用,需保存在寄存器中,因为寄存器的速度要比内存快的许多。在早期的编译器中需要手动定义为register型,但是后来编译器可以自动将调用次数多的变量放入寄存器中。
auto: 给变量动态分配内存,默认的分配类型。一般不需要手动声明了;
static:静态分配内存。变量在整个作用域内是全局变量。
extern :声明为外部变量;在函数的外部定义变量;
7.长为n的字符串中匹配长度为m的子串的复杂度为()
A.O(N)
B.O(M+N)
C.O(N+LOGM)
D.O(M+LOGN)
B.要好好研究一下KPM算法
8.判断一包含n个整数a[]中是否存在i、j、k满足a[i] + a[j] = a[k]的时间复杂度为()
A.O(n) B.O(n^2) C.O(nlog(n)) D.O(n^2log(n))
又是算法题:网上给的答案是B
9.三次射击能中一次的概率是0.95,请问一次射击能中的概率是多少?
A.0.63
B.0.5
C.0.32
D.0.85
这里能击中一次理解为至少能击中1次。否则如果理解为只能击中一次那么概率不会这么大。那么一次不中的话 (1-p)^3=0.05;得p在0.5和2/3之间,选A.
10.下列序排算法中最坏复杂度不是n(n-1)/2的是_
A.快速序排 B.冒泡序排 C.直接插入序排 D.堆序排
D. 堆排序的时间复杂度是n*lgn
二、不定项选择题
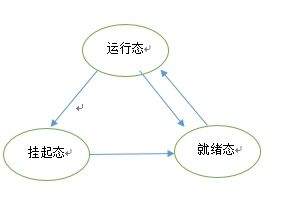
1. 阻塞、就绪、运行的三态转换
2.一个栈的入栈数列为:1、2、3、4、5、6;下列哪个是可能的出栈顺序。(选项不记得)
只要记得先进后出就可以了
3.下列哪些代码可以使得a和b交换数值。
有不使用第三个变量的;包括: a=a+b; b=a-b; a=a-b;
2) 通过异或运算。x=x^y; y=x^y; x=x^y;因为x^x=0;x^0=x;可以慢慢推出来结果。
4.A和B晚上无聊就开始数星星。每次只能数K个(20<=k<=30)A和B轮流数。最后谁把星星数完谁就获胜,那么当星星数量为多少时候A必胜?
A.2013 B.2886 C.4026 D......E.....(选项不记得)
不是很明白这道题的意思。
三、填空问答题
1.给你一个整型数组A[N],完成一个小程序代码(20行之内),使得A[N]逆向,即原数组为1,2,3,4,逆向之后为4,3,2,1;
此题较为简单,有一般程序设计基础的学生都可以做的出来。首尾交换就可以了
2.自选调度方面的问题,题目很长,就是给你三个线程,分别采用先来先分配的策略和最短执行之间的调度策略,然后计算每个线程从提交到执行完成的时间。题目实在太长,还有几个表格。考察的是操作系统里面作业调度算法先进先出和最短作业优先。
此题是操作系统中经典的线程调度问题,包括FIFO,SJF.还有包括最小剩余时间有限算法。电梯调度算法等。
3.有个苦逼的上班族,他每天忘记定闹钟的概率为0.2,上班堵车的概率为0.5,如果他既没定闹钟上班又堵车那他迟到的概率为1.0,如果他定了闹钟但是上班堵车那他迟到的概率为0.8,如果他没定闹钟但是上班不堵车他迟到的概率为0.9,如果他既定了闹钟上班又不堵车那他迟到的概率为0.0,那么求出他在60天里上班迟到的期望。
这是道简单的概率题:期望=概率*样本值;
所以迟到的天数=(0.2*0.5*1+0.8*0.5*0.8+0.2*0.5*0.9)*60=30.6
4.战报交流:战场上不同的位置有N个战士(n>4),每个战士知道当前的一些战况,现在需要这n个战士通过通话交流,互相传达自己知道的战况信息,每次通话,可以让通话的双方知道对方的所有情报,设计算法,使用最少的通话次数,是的战场上的n个士兵知道所有的战况信息,不需要写程序代码,得出最少的通话次数。
最直观的就是所有的人都相互交流过,那么这样的话时间复杂度是n(n-1)/2;
而如果是一个人先和所有的n-1个交流过充当中间人的作用,再和另外的n-1个再交流一次那么2(n-1)次即可完成复制;这时候因为 n>4所以2(n-1)
5.有N个人,其中一个明星和n-1个群众,群众都认识明星,明星不认识任何群众,群众和群众之间的认识关系不知道,现在如果你是机器人R2T2,你每次问一个人是否认识另外一个人的代价为O(1),试设计一种算法找出明星,并给出时间复杂度(没有复杂度不得分)。
答案:
最直观的解决方法是:找到那个任何人都不认识的就是明星;那么
1. 伪代码:
for i=[0,n-1){
flag=false; //标识i是否认识其他人,如果有认识的人则标识为true
for j=[1,n){
if(i认识j){
flag=true;
break;
}//end if }//end for
//判断i是否有认识的人
if(flag==false)
return i; //如果i在剩余的人中没有认识的人,则为明星
}//end for 这样的时间复杂度是:o(n*2)
但是这种方法没有充分利用条件:1.如果是明星的话,那么肯定不认识群众;2.如果是群众肯定认识明星。所以:
对于1个判断: a与b最多两种可能:1、a认识b,那么a不可能是明星;
2、a不认识b那么b不可能是明星。即每一次比较都会识别一个。所以最多0(n-1)即可识别出哪个是明星:
1. 伪代码:result=0; //i=0,初始化
2. //初始化栈,入栈
for i=[1,n) {
. stack.push(i);
. }//end for
. while(!stack.isEmpty()){
temp=stack.pop(); //出栈
//判断结果
if(temp 认识 result) //result可能是明星
result=result;
else //temp 不认识 result,则temp可能是明星
result=temp;
}//end while四、综合题
有一个淘宝商户,在某城市有n个仓库,每个仓库的储货量不同,现在要通过货物运输,将每次仓库的储货量变成一致的,n个仓库之间的运输线路围城一个圈,即1->2->3->4->...->n->1->...,货物只能通过连接的仓库运输,设计最小的运送成本(运货量*路程)达到淘宝商户的要求,并写出代码。
类似的题目:
有n个小朋友坐成一圈,每人有ai个糖果。每人只能给左右两人传递糖果。每人每次传
递一个糖果代价为1,求使所有人获得均等糖果的最小代价。
分析:
先求出来average;
从第一个开始顺时针传,如果刚好保证 a1=average;那么1需要传给2,a1-average个;这样2需要传给3, a2+(a1-average)-average个,3需要传给4,a3+a2+a1- 3*average..
但是这样做不一定准确,因为有可能最后一个是大于average的,导致中间会传负值,而且并不能保证这样一定是最小的。那么我们就假设最一般的现象:如果到最后a1需要传给an k个才能保证都达到average那么a1需要保留 average+k个因此需要传a1-average-k ,a2仍然保证最后留average个,那么需要传a1-average-k+a2-k个…
所需代价:|a1-k-ave|+|a1+a2-k-2*ave|+|a1+a2+a3-k-3*ave|+…+|a1+..+a(n-1)-k-(n-1)*ave|+|k|
以sum[i]表示从a1加到ai减掉i*ave的和值,这以上可以化简为
总代价 =|s1-k|+|s2-k|+...+|s(n-1)-k|+|k|
不难看出:当k为s1...s(n-1)中的中位数的时候,所需的代价最小:
代码转载于网络:
#include
#include
#include
using namespace std;
const int X = 1000005;
typedef longlong ll;
ll sum[X],a[X];
ll n;
ll Abs(ll x){
return max(x,-x);
}
int main(){
//freopen("sum.in","r",stdin);
while(cin>>n){
ll x;
ll tot = 0;
for(inti=1;i<=n;i++){
scanf("%lld",&a[i]);
tot += a[i];
}
ll ave = tot/n;
for(inti=1;i