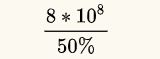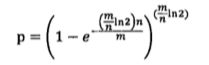布隆过滤器是由Burton Bloom与1970年提出来的,所以它的名字就叫做Bloom Filter。它实际上是一个很长的二进制向量和一系列的随机映射函数。
使用场景
- 有的黑客为了让服务宕机,他们会构建大量不存在于缓存中的key向服务器发起请求,在数据量足够大的情况下,频繁的数据库查询可能导致DB挂掉。布隆过滤器很好的解决了缓存击穿的问题。
- 反垃圾邮件,从数十亿个垃圾邮件列表中判断某个邮箱是否是垃圾邮箱。
- 网页爬虫对URL去重,防治爬取相同的URL地址
- ...
算法描述
一个空的布隆过滤器是由m个bits组成的bit array,每一个bit位都初始为0。并且定义有k个不同的哈希函数,每个哈希函数都将元素哈希到bit array的不同位置。
当添加一个元素时,用k个哈希函数分别将它hash得到k个bit位,然后将这些bit位置位1。
查询一个函数时,同样用k个哈希函数将它hash,再判断k个bit位上是否都为1,如果其中某一位为0,则该元素不存在于布隆过滤器中。
常规的布隆过滤器不允许执行删除元素操作,因为那样会把k个bits位置位0,而其中某一位可能和其他元素想对应。因此删除操作会引入false negative,如果需要删除操作可以使用Counting Bloom Filter
当k很大时,设计k个独立的哈希函数是不现实的。对于一个输出范围很大的哈希函数(MD5产生的128 bits),如果不同bits的相关性很小,则可以把此输出分割位k份。或者将k个不同的初始值结合元素,feed给一个哈希函数从而产生k个不同的值。
举例说明
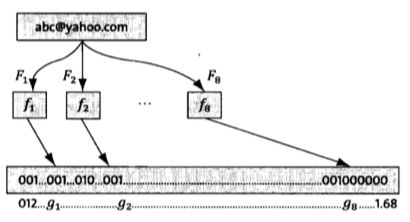
就以垃圾邮件过滤为例,假定我们有一亿个垃圾邮件地址,每个邮件用8个hash函数来生成8个信息指纹,因为在保证误判率低且k和m选取合适时,空间利用率为50%。所以我们的m(布隆过滤器的槽数)为,也就是16亿个二进制位。我们先将所有二进制位全部清零。对于每个邮件地址X,我们用8个不同的hash函数进行hash,再将这8个信息指纹映射到1-16亿中的8个自然数g1,g2,...g8。现在将这8个位置的二进制值全部置为1。对一亿个邮件地址都进行这样的处理后,我们的布隆过滤器也就建成功了。
当我们要判断一个邮件地址是否在布隆过滤器中时,需要使用相同的8个hash函数来将8个信息指纹对应到布隆过滤器的8个二进制位上。如果8个二进制位的值只要有一个或更多为0,那么它一定不存在于布隆中。如果8个值全都为1,那么它可能存在于布隆中,这是因为误识别导致的。
优势
相对于其它的数据结构,布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数。另外,hash函数相互之间没有关系,方便由硬件并行实现。布隆过滤器不需要存储数据本身,在某些对保密要求非常严格的场合由优势。
缺点
布隆过滤器的缺点和其优点一样明显。误算率(False Positive)是其中之一。随着存入元素的数量增加,误算率随之增加。
误判概率的证明和计算
在上面的案例中,我们说到过关于布隆的误算率的问题,这在检验上被称为假阳性。
估算假阳性的概率并不难。假定布隆过滤器有m比特,里面有n个元素,每个元素对应k个信息指纹的哈希函数,当然这里m比特里有些是0有些是1。我们先来看看某个比特为0的概率。当我们在插入一个元素时,它的第一个哈希函数会把过滤器中的某个比特置为1,因此,任何一个比特被置为1的概率是1/m,它依然为0的概率则为1-1/m。对于过滤器中的某个特定位置,如果这个元素k个哈希函数都没有把它设置为1,其概率是(1-1/m)^k。如果过滤器插入第二个元素,某个特定位置依然没有被设置为1,其概率为(1-1/m)^2k。如果插入了n个元素,还是没有把某个位置设置为1,其概率为(1-1/m)^kn。反过来,一个比特在插入了n个元素后,被置为1的概率为1-(1-1/m)^kn。
现在假定这n个元素都放到了过滤器中,新来一个不在集合中的元素,由于它的信息指纹的哈希函数都是随机的,因此,它的第一个哈希函数正好命中某个值为1的比特的概率就是上述概率。一个不在集合中的元素被误识别为在集合中,所需要的哈希函数对应比特的值均为1,其概率为:
化简后为:
如果n比较大,可以近似为:
PHP实现
class BloomFilterHash
{
/**
* 由Justin Sobel 编写的按位散列函数.
*
* @param string $string
* @param null $len
* @return int
*/
public function JSHash($string, $len = null)
{
$hash = 1315423911;
$len || $len = strlen($string);
for ($i = 0; $i < $len; $i ++) {
$hash ^= (($hash << 5) + ord($string[$i]) + ($hash >> 2));
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* 该哈希算法基于AT&T贝尔实验室的Peter J. Weinberger的工作。
* Aho Sethi和Ulman编写的“编译器(原理,技术和工具)”一书建议使用采用此特定算法中的散列方法的散列函数。
*
* @param string $string
* @param null $len
* @return int
*/
public function PJWHash($string, $len = null)
{
$bitsInUnsignedInt = 4 * 8;
$threeQuarters = ($bitsInUnsignedInt * 3) / 4;
$oneEighth = $bitsInUnsignedInt / 8;
$highBits = 0xFFFFFFFF << (int) ($bitsInUnsignedInt - $oneEighth);
$hash = 0;
$test = 0;
$len || $len = strlen($string);
for ($i = 0; $i < $len; $i ++) {
$hash = ($hash << (int) ($oneEighth)) + ord($string[$i]);
}
$test = $hash & $highBits;
if ($test != 0) {
$hash = (($hash ^ ($test >> (int)($threeQuarters))) & (~$highBits));
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* 类似PJW Hash功能,但是针对32位处理器做了调整。它是基于unix系统上的widely使用哈希函数。
*
* @param string $string
* @param null $len
* @return int
*/
public function ELEHash($string, $len = null)
{
$hash = 0;
$len || $len = strlen($string);
for ($i = 0; $i < $len; $i++) {
$hash = ($hash << 4) + ord($string[$i]);
$x = $hash & 0xF0000000;
if ($x != 0) {
$hash ^= ($x >> 24);
}
$hash &= ~$x;
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* 这个哈希函数来自Brian Kernighan和Dennis Ritchie的书“The C Programming Language”。
* 它是一个简单的哈希函数,使用一组奇怪的可能种子,它们都构成了31 .... 31 ... 31等模式,它似乎与DJB哈希函数非常相似。
*/
public function BKDRHash($string, $len = null)
{
$seed = 131; # 31 131 1313 13131 131313 etc..
$hash = 0;
$len || $len = strlen($string);
for ($i=0; $i<$len; $i++) {
$hash = (int) (($hash * $seed) + ord($string[$i]));
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* 这是在开源SDBM项目中使用的首选算法。
* 哈希函数似乎对许多不同的数据集具有良好的总体分布。它似乎适用于数据集中元素的MSB存在高差异的情况。
*/
public function SDBMHash($string, $len = null)
{
$hash = 0;
$len || $len = strlen($string);
for ($i=0; $i<$len; $i++) {
$hash = (int) (ord($string[$i]) + ($hash << 6) + ($hash << 16) - $hash);
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* 由Daniel J. Bernstein教授制作的算法,首先在usenet新闻组comp.lang.c上向世界展示。
* 它是有史以来发布的最有效的哈希函数之一。
*/
public function DJBHash($string, $len = null)
{
$hash = 5381;
$len || $len = strlen($string);
for ($i=0; $i<$len; $i++) {
$hash = (int) (($hash << 5) + $hash) + ord($string[$i]);
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* Donald E. Knuth在“计算机编程艺术第3卷”中提出的算法,主题是排序和搜索第6.4章。
*/
public function DEKHash($string, $len = null)
{
$len || $len = strlen($string);
$hash = $len;
for ($i=0; $i<$len; $i++) {
$hash = (($hash << 5) ^ ($hash >> 27)) ^ ord($string[$i]);
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
/**
* 参考 http://www.isthe.com/chongo/tech/comp/fnv/
*/
public function FNVHash($string, $len = null)
{
$prime = 16777619; //32位的prime 2^24 + 2^8 + 0x93 = 16777619
$hash = 2166136261; //32位的offset
$len || $len = strlen($string);
for ($i=0; $i<$len; $i++) {
$hash = (int) ($hash * $prime) % 0xFFFFFFFF;
$hash ^= ord($string[$i]);
}
return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF;
}
}
abstract class BloomFilterRedis
{
/**
* 需要使用一个方法来定义bucket名字.
*/
protected $bucket;
protected $hashFunction;
public function __construct()
{
if (!$this->bucket || !$this->hashFunction) {
throw new Exception("需要定义bucket和hashFunction");
}
$this->Hash = new BloomFilterHash;
$this->Redis = new \Redis(); // 假设已经连接好了
$this->Redis->connect('127.0.0.1');
}
/**
* @param $string
* @return array
*/
public function add($string)
{
$pipe = $this->Redis->multi();
foreach ($this->hashFunction as $function) {
$hash = $this->Hash->$function($string);
$pipe->setBit($this->bucket, $hash, 1);
}
return $pipe->exec();
}
/**
* 查询是否存在,不存在的一定不存在,存在的可能存在误判.
*
* @param $string
* @return bool
*/
public function exists($string)
{
$pipe = $this->Redis->multi();
$len = strlen($string);
foreach ($this->hashFunction as $function) {
$hash = $this->Hash->$function($string, $len);
$pipe = $pipe->getBit($this->bucket, $hash);
}
$res = $pipe->exec();
foreach ($res as $bit) {
if ($bit == 0) {
return false;
}
}
return true;
}
}
class FilteRepeatedComments extends BloomFilterRedis
{
protected $bucket = 'rptc';
protected $hashFunction = array('BKDRHash', 'SDBMHash', 'JSHash');
}
小结
源码地址:https://gitee.com/pchangl/Bloom-Filter-Demo