作者:每天3道奥数题
链接:https://www.zhihu.com/question/29868843/answer/380902927
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
先从一个赌博游戏讲起:
假如有一天,马阿里突然要和你玩个抛硬币的投注游戏,规则是这样的:如果硬币正面朝上,马阿里就给你投注金额5倍的钱;如果硬币反面朝上,你所有下注的钱就归马阿里所有。问题的关键在于:下不下注?用多少钱下注?
要回答这个问题,必须从概率说起了。世界是由无数个偶然事件构成的,为了描述这种偶然性,数学家发明了概率。从某种意义上来说,人生就是一场概率游戏,投资的本质也是投概率。
- 一、零概率事件也可能发生
给定一根长度为1的线段,用一支无限小的针去扎这条线段,任何一个点都有可能被扎到,但扎到任何一个点的概率都是0。
因此,零概率事件也是可能发生的,反过来说,概率为100%的事件也有可能不发生。
为了不让小概率事件毁掉你的一切,你必须熟记理财中的那句经典名言:“不要把鸡蛋放在一个篮子里。”
由此引申出来的是:
用适当的钱买点保险很有必要,这是应对意外发生的最简单同时也是最好的办法;
家里储藏一点实物黄金也是很有必要的,这是用来应对战乱、饥荒等极小概率事件的有效手段,但最好祈祷这些黄金永远用不到;
银行里随时备有可供家庭支出3个月左右的活期存款还是很有必要的,这是用来应付意外失业的;
理财的钱要分散的投资于银行定期存款、银行理财、房市、信托、股市、债市、网络理财平台等,这是用来应付像股灾那样的崩塌性小概率事件。
……二、数学期望决定了是否进行投资
文章开头的抛硬币游戏,之所以看起来划算,是因为我们认为硬币正面朝上和反面朝上的概率是一样的,都是1/2,而正面朝上可以得到5倍回报,所以,回报是大于投入的。
回报到底有多大?数学期望就是这样一个衡量指标。通俗的来说,数学期望就是回报的平均值。如果回报为a(i)的概率是p(i),其计算公式就是:
E=a(1)p(1)+a(2)p(2)+…+a(n)*p(n)
在抛硬币游戏中,如果投入1元,回报的数学期望就是:
51/2-11/2=2元。
这个回报的数学期望是大于投入的,所以,参与游戏是能赚到钱的。
因此,判断一项投资是否划算,关键是计算数学期望与投入的关系,只有回报的数学期望大于投入时,才能进行投资。
从另一个角度看,数学期望可以用来估计资产的价格。比如有一项资产,有60%的概率挣到100万,有20%的概率挣到200万,有10%的概率不赚不赔,有10%的概率亏损500万,那这项资产值得用多少钱来购买?
由于其数学期望是:
10060%+20020%+010%-50010%=50,
因此,只要价格不高于50万元,这项资产都是值得购买的。
- 三、凯利公式告诉你投资的仓位
我们已经知道,文章开头的抛硬币游戏是一项能赚到钱的投资。现在考虑一个问题:假如你有1万元,为了保证在有限次游戏中收益的最大化,你每次该用多少钱去参与?
要是全部投入,一把梭哈,那万一全亏了怎么办?
要是投资少了,机会难得,赚少了就只能自己后悔!
数学中, “凯利公式”就是用来解决这个问题的!这个公式是教你风险控制的方法,让你在确保不爆仓的前提下,得到收益最大化。
先给出凯利公式的表达式:
f=(ap-bq)/(ab),
其中f就是投入的最佳仓位,
a表示本金收益率(赌博中叫赔率),
b表示本金损失率(赌博中b为1),
p表示获得正收益的概率,
q表示获得亏损的的概率。
在抛硬币的游戏中,a=5,b=1,p=q=1/2,容易计算得到f=40%。
所以,每次用4成的仓位去玩抛硬币的游戏才可以使收益最大化。
凯利公式的证明非常复杂,需要用到中心极限定理和正态分布等概率学知识,而且证明的过程也特别数学,这里就不再啰嗦。
马阿里的抛硬币游戏在生活中不常见,但投资的机会在生活中比比皆是。在股票、期货等投资中,凯利公式常常被用来进行仓位控制。
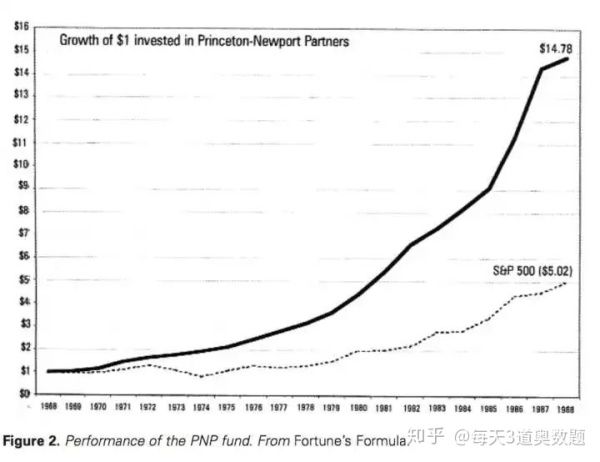
量化基金的鼻祖,天才数学家索普,就曾将凯利公式应用的出神入化。他先是自学编程,利用早期的IBM大型机,开发了一套专门用于21点的算法,然后用其在拉斯维加斯大把吸金,甚至因为赢钱太多一度被多家大型赌场列入黑名单拒绝入内,电影《决胜21点》就是以此为原型拍摄的。后来,他又成立了著名的量化基金PNP(PrincetonNewport Partners),应用凯利公式,在资本市场大杀四方,下图就是PNP基金的净值曲线。
不过,应用凯利公式最大的问题就是要知道慨率。数学题目中,概率都是已知的,但资本市场是千变万化的,概率并不知道,这就需要用到数学中的另外一个大杀器——大数定律。
- 四、大数定律告诉你怎么计算概率
太阳底下没有新鲜事!
历史总是在不断的重复,从历史中我们能够得到足够多的样本数据。
大数定律告诉我们,当样本数据足够多的时候,频率总是无限的趋近于概率。因此,用历史频率代替概率是科学可行的。
比如在股票的量化交易中,一种最简单的投资模型如下:
假设过去一段时间的最高价为m,最低价为n,当前价格为k。
正收益率用a=(m-k)/k表示,
亏损率用b=(k-n)/k表示,
赚钱和亏钱的概率分别用过去5年来的5日盈亏情况的频率替代,
最佳仓位f就可以用凯利公式进行计算并实时调整了。
真实的量化交易模型,比上面的要复杂很多,也精细很多,但万变不离其宗,凯利公式都是风险控制的不二法门。