上一篇文章给出了一个基本的分布算法,虽然可以求出结果最优的分布,但是还存在一个严重缺陷:没有考虑数据原来的分布情况。
当集群新加入一批机器或者有机器故障的时候,数据要重新分布,如果使用前文算法,由于没有考虑数据原来的分布情况,即使是集群发生微小的变动,也会导致所有数据的位置改变,这显然是不可接受的。所以分布算法应该在结果最优的情况下,使得数据位置的变动尽量少。
我优化的思路是:尽量让桶留在原来的机器上。为此,我对原来的模型做了一些改变:
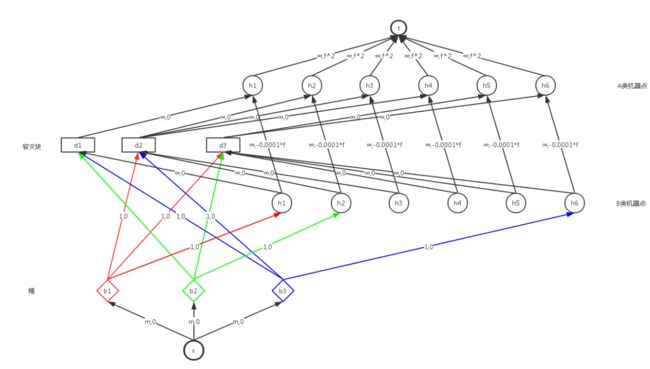
增加一组节点,每台机器对应其中一个节点,把原来的机器节点叫A类机器节点,新增加的这组节点叫做B类机器节点。
B类每个节点向A类对应的节点连一条不限流量、费用为-0.0001的边。
B类每个节点向机器所在的容灾块连一条不限流量、费用为0的边。
如果目前一个桶b在机器h上有一个副本,机器属于容灾块d,那么前文模型中原本应该从b连到d的边改为从b连到B类h节点。
经过上述修改后,流会尽量选择有负费用的道路,根据求出的最小费用最大流,就会对应一个副本位置尽量不变的最优分布方案。
上图中,桶b1在机器h1上有一个副本,所以b1到h1有一条边,b1到d1的没有了。同理,b2在h2有一个副本,b3在h6有一个副本。
加了这个优化,本算法就基本可以满足实际需要了。
算法复杂度
有n个桶,每个桶有m份副本,有s台机器
那么所建的图共有nm+2s个点(容灾块较少,可忽略)
需要对这个图做nm次增广,故理论复杂度为O(nm(nm+2*s)^2)
但由于图的结构特殊,性能还有进一步优化的空间,这就要看实际情况了。
代码
先是公用的头文件
#include
struct ScheduleTable
{
//分布表,一行表示一个桶的分布,每列上的值代表这个桶的一个副本所在的机器
//第0列表示这个桶主副本所在的机器,机器编号全部大于0,表中的0表示该副本不在任何机器上。
ScheduleTable(unsigned int row, unsigned int col)
{
this->row = row;
this->col = col;
this->arr = static_cast(calloc(row * col, sizeof(unsigned int)));
}
ScheduleTable(const ScheduleTable& table)
{
this->row = table.row;
this->col = table.col;
this->arr = static_cast(calloc(row * col, sizeof(unsigned int)));
memmove(this->arr, table.arr, row * col * sizeof(unsigned int));
}
~ScheduleTable()
{
free(arr);
}
unsigned int* operator [](unsigned int index) const
{
return arr + index * col;
}
unsigned int get_row()
{
return row;
}
unsigned int get_col()
{
return col;
}
unsigned int* arr;
private:
unsigned int row, col;
};
//机器信息
struct DataNodeInfo
{
unsigned int id;//机器编号
unsigned int groupid;//容灾块编号
};
接着算法代码代码
#include
#include
#include
#include
#include
#include 测试
用gtest做了几个单元测试
#include
#include
#include "gtest/gtest.h"
#include "schedule_table.h"
using namespace std;
class ScheduleTest: public testing::Test
{
public:
static const int ROW = 1024;//桶个数
static const int COL = 3;//副本数
static const int NODES = 1024;//机器编号范围[1, NODES - 1]
static unsigned int nodes[NODES];//nodes[i]不为0表示存在编号为i的机器,nodes[i]为机器的groupid
static unsigned int nodes_count;
static ScheduleTable table;
static void SetUpTestCase()
{
}
virtual void SetUp()
{
}
virtual void TearDown()
{
}
static void del_node(unsigned int num, unsigned int group_id);
static void add_node(unsigned int num, unsigned int group_id);
static void get_node(vector &vec);
static int check(bool print_state);
static int check_zero();
static void print_state();
static void check_diff(ScheduleTable &t1, ScheduleTable &t2);
};
unsigned int ScheduleTest::nodes[NODES];
unsigned int ScheduleTest::nodes_count;
ScheduleTable ScheduleTest::table(ROW, COL);
extern int select_master(ScheduleTable &table, const vector &nodes, ScheduleTable* old_table = NULL);
extern int fix_and_balance(ScheduleTable &table, const vector &nodes);
void ScheduleTest::del_node(unsigned int num, unsigned int group_id)
{
int i, j, m, n, st;
for (i = 0; nodes_count && i < num; i++)
{
st = rand() % nodes_count;
for (j = 1; j < NODES; j++)
if (nodes[j])
{
if (st == 0)
break;
--st;
}
while (nodes[j] != group_id)
j = (j + 1) % NODES;
for (m = 0; m < ROW; m++)
for (n = 0; n < COL; n++)
{
if (table[m][n] == j)
table[m][n] = 0;
}
nodes[j] = 0;
nodes_count--;
}
}
void ScheduleTest::add_node(unsigned int num, unsigned int group_id)
{
for (int i = 1; num && i < NODES; i++)
if (nodes[i] == 0)
{
nodes[i] = group_id;
num--;
nodes_count++;
}
}
void ScheduleTest::get_node(vector &vec)
{
vec.clear();
for (unsigned int i = 1; i < NODES; i++)
if (nodes[i])
vec.push_back((DataNodeInfo){i, nodes[i]});
}
void ScheduleTest::check_diff(ScheduleTable &t1, ScheduleTable &t2)
{
unsigned int mdiff = 0;
unsigned int diff = 0;
for (unsigned int i = 0; i < ROW; i++)
{
if (t1[i][0] != t2[i][0])
mdiff++;
for (unsigned int j = 0; j < t1.get_col(); j++)
{
unsigned int k;
for (k = 0; k < t2.get_col(); k++)
if (t1[i][j] == t2[i][k])
break;
if (k == t2.get_col())
diff++;
}
}
printf("%d master will change\n%d buckets will change or add\n", mdiff, diff);
}
int ScheduleTest::check_zero()
{
for (unsigned int i = 0; i < ROW; i++)
for (unsigned int j = 1; j < COL; j++)
if (table[i][j] == 0)
return 1;
return 0;
}
int ScheduleTest::check(bool print_state = false)
{
unsigned int s[NODES], m[NODES];
memset(s, 0, sizeof(s));
memset(m, 0, sizeof(m));
for (unsigned int i = 0; i < ROW; i++)
{
m[table[i][0]]++;
for (unsigned int j = 0; j < COL; j++)
{
for (unsigned int k = j + 1; k < COL; k++)
if (nodes[table[i][j]] == nodes[table[i][k]])
return 1;
s[table[i][j]]++;
}
}
//统计每台机器的主副本数和副本数
if (print_state)
for (unsigned int i = 0; i < NODES; i++)
if (nodes[i])
printf("%d/%d: %d %d\n", nodes[i], i, m[i], s[i]);// 容灾块编号/机器编号: 主副本数 副本数
return 0;
}
//初始化集群
TEST_F(ScheduleTest, init)
{
add_node(10, 1);
add_node(7, 2);
add_node(8, 3);
add_node(12, 4);
add_node(10, 5);
vector vec;
get_node(vec);
ASSERT_EQ(fix_and_balance(table, vec), 0);
ASSERT_EQ(check_zero(), 0);
ASSERT_EQ(check(true), 0);
}
//四台机器丢失,重新选主以恢复服务
TEST_F(ScheduleTest, del_4_select_master)
{
del_node(4, 4);
vector vec;
get_node(vec);
ScheduleTable old_table(table);
ASSERT_EQ(select_master(table, vec), 0);
ASSERT_EQ(check(true), 0);
check_diff(table, old_table);
}
//补全缺少的副本
TEST_F(ScheduleTest, fix_and_ballance)
{
vector vec;
get_node(vec);
ScheduleTable old_table(table);
ASSERT_EQ(fix_and_balance(table, vec), 0);
ASSERT_EQ(check_zero(), 0);
ASSERT_EQ(check(true), 0);
check_diff(table, old_table);
}
//集群扩容
TEST_F(ScheduleTest, add_8_30_8_ballance)
{
add_node(8, 5);
add_node(30, 6);
add_node(8, 7);
vector vec;
get_node(vec);
ScheduleTable old_table(table);
ASSERT_EQ(fix_and_balance(table, vec), 0);
ASSERT_EQ(check_zero(), 0);
ASSERT_EQ(check(true), 0);
check_diff(table, old_table);
}
//集群大规模扩容
TEST_F(ScheduleTest, add_many_host_ballance)
{
add_node(8, 5);
add_node(4, 6);
add_node(4, 7);
add_node(10, 4);
add_node(20, 7);
add_node(18, 8);
add_node(5, 9);
add_node(35, 10);
add_node(30, 11);
add_node(100, 12);
add_node(50, 13);
add_node(200, 14);
add_node(200, 15);
add_node(200, 16);
vector vec;
get_node(vec);
ScheduleTable old_table(table);
ASSERT_EQ(fix_and_balance(table, vec), 0);
ASSERT_EQ(check_zero(), 0);
ASSERT_EQ(check(), 0);
check_diff(table, old_table);
}
//后面的测例当有机器丢失后直接fix_and_ballance,只是为了测试方便
//实际上当有机器丢失后,都应该先选主快速恢复服务,再修复缺失的副本
//两个容灾块丢失,重置后重新加入集群
TEST_F(ScheduleTest, del_200_200_add_200_200_fix_and_ballance)
{
del_node(200,15);
del_node(200, 16);
add_node(200, 15);
add_node(200, 16);
vector vec;
get_node(vec);
ScheduleTable old_table(table);
ASSERT_EQ(fix_and_balance(table, vec), 0);
ASSERT_EQ(check_zero(), 0);
ASSERT_EQ(check(), 0);
check_diff(table, old_table);
}
//100台机器下线,加入140台新机器
TEST_F(ScheduleTest, del_100_add_70_70_fix_and_ballance)
{
del_node(100, 14);
add_node(70, 5);
add_node(70, 17);
vector vec;
get_node(vec);
ScheduleTable old_table(table);
ASSERT_EQ(fix_and_balance(table, vec), 0);
ASSERT_EQ(check_zero(), 0);
ASSERT_EQ(check(), 0);
check_diff(table, old_table);
}
//丢失1台机器,选主快速恢复服务
TEST_F(ScheduleTest, del_1_select_master)
{
del_node(1, 17);
vector vec;
get_node(vec);
ScheduleTable old_table(table);
ASSERT_EQ(select_master(table, vec), 0);
ASSERT_EQ(check(), 0);
check_diff(table, old_table);
}
//修复缺失副本
TEST_F(ScheduleTest, fix_and_ballance2)
{
vector vec;
get_node(vec);
ScheduleTable old_table(table);
ASSERT_EQ(fix_and_balance(table, vec), 0);
ASSERT_EQ(check_zero(), 0);
ASSERT_EQ(check(), 0);
check_diff(table, old_table);
}
测试结果
对于集群规模较小的测例打印出了具体分布情况
格式:“容灾块编号/机器编号: 主副本数 副本数”
Running main() from gtest_main.cc
[==========] Running 9 tests from 1 test case.
[----------] Global test environment set-up.
[----------] 9 tests from ScheduleTest
[ RUN ] ScheduleTest.init
1/1: 22 66
1/2: 22 66
1/3: 21 66
1/4: 22 66
1/5: 22 66
1/6: 22 66
1/7: 22 65
1/8: 21 65
1/9: 22 65
1/10: 21 65
2/11: 22 66
2/12: 22 66
2/13: 22 66
2/14: 21 66
2/15: 22 66
2/16: 22 66
2/17: 21 65
3/18: 21 66
3/19: 22 66
3/20: 22 66
3/21: 22 66
3/22: 22 66
3/23: 21 65
3/24: 21 65
3/25: 21 65
4/26: 22 65
4/27: 22 65
4/28: 22 65
4/29: 22 65
4/30: 22 65
4/31: 22 65
4/32: 22 65
4/33: 22 65
4/34: 21 65
4/35: 22 65
4/36: 22 65
4/37: 22 65
5/38: 22 65
5/39: 22 65
5/40: 22 65
5/41: 22 65
5/42: 22 65
5/43: 22 65
5/44: 22 65
5/45: 22 65
5/46: 22 65
5/47: 22 65
node count: 47
[ OK ] ScheduleTest.init (1804 ms)
[ RUN ] ScheduleTest.del_4_select_master
1/1: 24 66
1/2: 24 66
1/3: 24 66
1/4: 24 66
1/5: 24 66
1/6: 24 66
1/7: 24 65
1/8: 24 65
1/9: 24 65
1/10: 23 65
2/11: 23 66
2/12: 24 66
2/13: 24 66
2/14: 23 66
2/15: 24 66
2/16: 24 66
2/17: 24 65
3/18: 23 66
3/19: 24 66
3/20: 24 66
3/21: 24 66
3/22: 24 66
3/23: 24 65
3/24: 24 65
3/25: 23 65
4/30: 23 65
4/31: 23 65
4/32: 24 65
4/33: 24 65
4/34: 23 65
4/35: 24 65
4/36: 24 65
4/37: 24 65
5/38: 24 65
5/39: 24 65
5/40: 24 65
5/41: 24 65
5/42: 24 65
5/43: 24 65
5/44: 24 65
5/45: 24 65
5/46: 24 65
5/47: 24 65
node count: 43
106 master will change
0 buckets will change or add
[ OK ] ScheduleTest.del_4_select_master (621 ms)
[ RUN ] ScheduleTest.fix_and_ballance
1/1: 24 71
1/2: 24 71
1/3: 24 71
1/4: 24 71
1/5: 24 71
1/6: 24 71
1/7: 24 71
1/8: 24 71
1/9: 24 71
1/10: 23 71
2/11: 23 72
2/12: 24 72
2/13: 24 72
2/14: 23 72
2/15: 24 72
2/16: 24 72
2/17: 24 72
3/18: 23 72
3/19: 24 72
3/20: 24 72
3/21: 24 72
3/22: 24 72
3/23: 24 72
3/24: 24 72
3/25: 23 72
4/30: 23 72
4/31: 23 72
4/32: 24 72
4/33: 24 72
4/34: 23 71
4/35: 24 71
4/36: 24 71
4/37: 24 71
5/38: 24 71
5/39: 24 71
5/40: 24 71
5/41: 24 71
5/42: 24 71
5/43: 24 71
5/44: 24 71
5/45: 24 71
5/46: 24 71
5/47: 24 71
node count: 43
0 master will change
271 buckets will change or add
[ OK ] ScheduleTest.fix_and_ballance (3489 ms)
[ RUN ] ScheduleTest.add_8_30_8_ballance
1/1: 12 35
1/2: 12 35
1/3: 12 35
1/4: 12 35
1/5: 12 35
1/6: 12 35
1/7: 12 35
1/8: 12 35
1/9: 12 35
1/10: 12 35
2/11: 12 35
2/12: 12 35
2/13: 12 35
2/14: 12 35
2/15: 12 35
2/16: 12 35
2/17: 12 35
3/18: 12 35
3/19: 12 35
3/20: 12 35
3/21: 12 35
3/22: 12 35
3/23: 12 35
3/24: 12 35
3/25: 12 35
5/26: 11 35
5/27: 11 34
5/28: 11 34
5/29: 11 34
4/30: 12 35
4/31: 12 35
4/32: 12 35
4/33: 12 35
4/34: 12 35
4/35: 12 35
4/36: 12 35
4/37: 12 35
5/38: 12 35
5/39: 12 35
5/40: 12 35
5/41: 12 35
5/42: 12 35
5/43: 12 35
5/44: 12 35
5/45: 12 35
5/46: 12 35
5/47: 12 35
5/48: 12 34
5/49: 12 34
5/50: 11 34
5/51: 11 34
6/52: 11 35
6/53: 11 34
6/54: 11 34
6/55: 11 34
6/56: 11 34
6/57: 11 34
6/58: 11 34
6/59: 11 34
6/60: 11 34
6/61: 11 34
6/62: 11 34
6/63: 11 34
6/64: 11 34
6/65: 11 34
6/66: 11 34
6/67: 11 34
6/68: 11 34
6/69: 11 34
6/70: 11 34
6/71: 11 34
6/72: 11 34
6/73: 11 34
6/74: 11 34
6/75: 11 34
6/76: 11 34
6/77: 11 34
6/78: 11 34
6/79: 11 34
6/80: 11 34
6/81: 11 34
7/82: 11 35
7/83: 11 34
7/84: 11 34
7/85: 11 34
7/86: 11 34
7/87: 11 34
7/88: 11 34
7/89: 11 34
node count: 89
508 master will change
1567 buckets will change or add
[ OK ] ScheduleTest.add_8_30_8_ballance (3190 ms)
[ RUN ] ScheduleTest.add_many_host_ballance
node count: 973
884 master will change
2716 buckets will change or add
[ OK ] ScheduleTest.add_many_host_ballance (6122 ms)
[ RUN ] ScheduleTest.del_200_200_add_200_200_fix_and_ballance
node count: 973
454 master will change
1200 buckets will change or add
[ OK ] ScheduleTest.del_200_200_add_200_200_fix_and_ballance (8025 ms)
[ RUN ] ScheduleTest.del_100_add_70_70_fix_and_ballance
node count: 1013
226 master will change
420 buckets will change or add
[ OK ] ScheduleTest.del_100_add_70_70_fix_and_ballance (9646 ms)
[ RUN ] ScheduleTest.del_1_select_master
node count: 1012
1 master will change
0 buckets will change or add
[ OK ] ScheduleTest.del_1_select_master (519 ms)
[ RUN ] ScheduleTest.fix_and_ballance2
node count: 1012
0 master will change
3 buckets will change or add
[ OK ] ScheduleTest.fix_and_ballance2 (10056 ms)
[----------] 9 tests from ScheduleTest (43472 ms total)
[----------] Global test environment tear-down
[==========] 9 tests from 1 test case ran. (43472 ms total)
[ PASSED ] 9 tests.
1000台机器、3000个副本,选主需要0.5s,算分布表需要10s
补充
对于超大集群,根据实际情况,还有很多优化可以做,这里乱说一个未经实践过的想法吧:首先排除有个容灾块拥有超过1/m的机器,导致最优分布也不是平均的极端情况。在此前提下,先用贪心之类的算法算出一个分布方案,然后从不同的容灾块中挑出总共300台副本数超过平均数机器,再从不同的容灾块中挑出若干台副本数小于平均数的机器,使得它们合在一起的平均数正好相当于全集群的平均数。
现在我们有了一个几百台机器的集合,找出m个副本都在这个集合的机器上的所有桶,用上文算法求一下这个子集的最优解。
重复上面的过程(可能可以用多线程加速一下),应该能得到满意的分布方案。