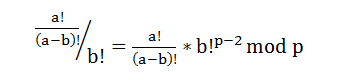大数组合取模,Lucas定理,费马小定理的运用

从一个例题：【HDU 3037】 Saving Beans 来开始Lucas定理的应用。
题目大意为：松鼠要从n棵树上摘一共m个豆子，结果的方案数对素数p（不大于1e5）取模，求解。
思路：
可以理解为m个豆子分为n份，求分的方法个数。
由插板法来对m个数进行划分，由于可能某棵树没有摘豆子，可以理解为：x1+x2+x3+……+xn=m的解的个数，即为C(m+n-1,n-1)。（将m颗豆子加上n-1个板子的位置，得到的序列再从中取n-1个板子的位置）=C(m+n-1,m)。
由于m的值取0~m，那么就得sum=C(n-1,0)+C(n,1)+C(n+1,2)+C(n+2,3)+……+C(m+n-1,m)。
利用公式C（n，r）=C（n-1，r）+C（n-1，r-1）=C（n-1，r）+C（n-2，r-1）+C（n-3，r-2）……
sum=C（n+m，m）。
也就是说，接下来的算法变成了C（n+m，m）%p。
然后就是Lucas定理的运用：
Lucas（m，n，p）=C（m%p，n%p，p）✲Lucas（m/p，n/p，p）。
Lucas（x，0，p）=1。
这里可以采用的方法是递归求解。
简单的理解就是：
以求解n! % p 为例，把n分段，每p个一段，每一段求得结果是一样的。但是需要单独处理每一段的末尾p,2p,...,把p提取出来，会发现剩下的数正好又是(n/p)! ，相当于划归了一个子问题，这样递归求解即可。
这个是单独处理n！的情况，当然C(n,m)就是n！/(m! *（ｎ－ｍ）！），每一个阶乘都用上面的方法处理的话，就是Lucas定理了.
Lucas最大的数据处理能力是p在10^5左右。
而C(a,b) =a! / ( b! ✲ (a-b)! ) mod p
其实就是求 ( a! / (a-b)!) ✲ ( b! )^(p-2) mod p

上面这一步变换是根据费马小定理：假如p是质数，且a,p互质，那么a的（p-1）次方除以p的余数恒为1,
那么a和a^(p-2)互为乘法逆元，则（b / a) = (b * a^(p-2) ) mod p)

代入题目中：有

假设p与b！互质，那么b！与（p-2）互为逆元，有：

b!与b!^{(p-2)互为乘法逆元，即b!✲b!}(p-2)=1，那么，

//快速幂a^b % k

ll PowerMod(ll a, ll b, ll k) {
    ll tmp = a, ret = 1;
    while (b) {
        if (b & 1) ret = ret * tmp % k;
        tmp = tmp * tmp % k;
        b >>= 1;
    }
    return ret;
}

//求C(n, m)%p p最大为10^5 n, m可以很大！

ll Lucas(ll n, ll m, ll p) {
    ll ret = 1;
    while (n && m) {
        ll nn = n%p, mm = m%p;
        if (nn < mm) return 0;
        //fac[nn]为预处理的 fac[n] = n!%p 
        ret = ret*fac[nn]*PowerMod(fac[mm]*fac[nn-mm]%p, p-2, p)%p;
        n /= p;
        m /= p;
    }
    return ret;
}
//C(n, m) % p
Lucas(n, m, p);

用下面的Lucas定理程序实现就能得出结果，实现过程中要注意乘法时的强制转换

#include 
#include 

typedef long long lld;
lld N,M,P;

int Pow(lld a,lld n,lld p)
{
    lld x = a;
    lld res = 1;
    while(n)
    {
        if(n & 1)
        {
            res = ((lld)res * (lld)x) % p;
        }
        n >>= 1;
        x = ((lld)x*(lld)x) % p;
    }
    return res;
}

int Cm(lld n,lld m,lld p)
{
    lld a = 1,b = 1;
    if(m > n) return 0;
    //实现(a!/(a-b)!) * (b!)^(p-2)) mod p,由于n比较大，所以，此处不知道有什么好的优化
    while(m)
    {
        a = (a * n) % p;
        b = (b * m) % p;
        m--;
        n--;
    }
    return ((lld)a * (lld)Pow(b,p-2,p))%p;
}

int Lucas(lld n,lld m,lld p)
{
    if(m==0)
        return 1;
    return((lld)Cm(n%p,m%p,p)*(lld)Lucas(n/p,m/p,p))%p;
}

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%I64d%I64d%I64d",&N,&M,&P);
        printf("%d\n",Lucas(N+M,M,P));
    }
    return 0;
}