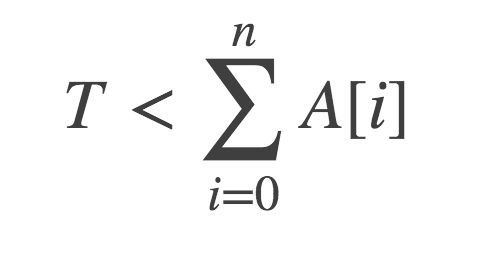详细的代码讲解和调试演示请参看视频:
如何进入google,算法面试技能全面提升指南
假设你是知名互联网公司BAT的首席财务官,公司去年的薪资成本是S,由于竞争激烈,公司今年需要成本控制,CEO要求你把总薪资控制为T, T < S。同时CEO希望你对每位员工的收入设定一个截断值P, 每一个年收入高于P的员工,其年薪一律降到P,对于那些年薪达不到P的,薪资保持不动。例如给定五位员工的薪资数值分别为:90, 30, 100, 40, 20, 同时T设置为210,那么截断值可以设置为60,也就是工资高于60的,全部降低到60,工资低于60的,收入保持不变,于是五位员工的收入变为:60, 30, 60, 40, 20,总薪资加总正好是210. 于是当CEO把所有员工工资交给你,并把总薪资控制水平T告诉你,你是否能找到对应的截断点?
对问题的数学化描述是,假设数组A包含有n个非负实数,同时给定一个值T,而且
设计一个有效算法找到截断值P, 使得:
这道题难度不小,如果不是题目提示使用二分查找法的话,我们很难往这个方向去思考。我们以前说过,遇到包含数组的算法题,首先想到的是先把它排序后看看有没有线索,由于我们需要使用二分查找,因此排序是必须的,以上面为例,我们先把员工的工资排序:
20,30,40,90,100
给定总和是210时,我们已经知道,截断值是60,并且是把90及其后面的数值全都改成60,这里我们把90这个元素称之为截断点。如何找到截断点并确定截断值呢?首先能确认的是,截断值一定不超过比截断点原来的值,并且大于截断点前面元素的值,例如60就小于截断点的值90,并且比截断点前面元素40要大。
如果顺着条件去思考的话,你会很难找到破解的线索,如果反过来,我们先随意找某个元素作为截断点,设置一个新的截断值,这样就得到一个新的总值T。然后在反过来思考,给定总值T后,我们如何找到截断点和相应的截断值。例如,假设我们把元素40当做截断点,设置35为阶段值,那么数组变为:
20, 30, 35,35,35
同时 T = 20 + 30 + 35 + 35 + 35 = 155.
于是问题反过来问,当给定新的总值是155时,我们如何确定截断点就在元素40处,并且截断值应该设置为35?
我们把两个数组并列在一起比较看看:
20, 30, 40, 90,100
20, 30,35 ,35, 35 T = 155
假设截断点不在40, 而是在40后面的元素90,那么我们会得到什么启示呢?如果截断点不在40的话,那么第二个数组中的35必须转变回40,又因为T=155必须保持不变,于是后面两个35必须抽出一部分数组给第一个35,让它增长到40,由于从截断点开始,后面的元素都必须保持一致,因此后两个35都必须各自拿出2.5添加到第一个 35上,于是数组变为:
20, 30, 40, 32.5, 32.5 T = 155
看到问题了把,此时的截断值比它前面的元素值要小,这根我们前面所总结的截断值性质是矛盾的,因此我们得出90肯定不会是截断点。那么如果我们假设40前面的30是截断点呢?由于从截断点元素开始,后续所有元素都要变成同一个截断值,因此为了保持总量不变T= 155不变,三个35,每个必须抽取出一部分补贴元素30,于是后面每个元素各自拿出1.25添加到元素30上,于是数组变成:
20, 33.75, 33.75, 33.75, 33.75
看到问题了吧,截断值居然比截断点原来的值要大,这与我们前面总结的阶段点性质矛盾。
由此,我们就找到一个二分查找截断点的办法,给定一个含有n个元素的数组以及一个新的总值T, 我们先假设数组中点是截断点,那么用(T - (A[0] + A[1] + ... +A[n/2-]) ) / (n/2) 得到截断值,公式中(n/2)是包括中点以及后续元素的总个数,得到截断值后我们看看,如果截断值比截断点前面元素的值要小,那么我们可以确定,截断点一定在当前点的左边,于是对左半边数组进行二分查找,如果截断值比截断点原来的值还要大,那么我们确定,正确的截断点一定在当前点的右边,于是我们可以对右半边数组使用二分查找法来进行查找。根据算法描述,我们给出算法的java实现:
import java.util.Arrays;
public class SalaryCap {
private int[] salaryArray;
private int salaryTotalCap;
private int[] salarySum;
public SalaryCap(int[] salaries, int capTotal) throws Exception {
this.salaryArray = salaries;
this.salaryTotalCap = capTotal;
Arrays.sort(this.salaryArray);
this.salarySum = new int[salaries.length];
int sum = 0;
for (int i = 0; i < this.salaryArray.length; i++) {
sum += this.salaryArray[i];
this.salarySum[i] = sum;
}
if (capTotal >= sum) {
throw new Exception("Capped Salary is highter than original salary sum");
}
}
public float getSalaryCap() {
int begin = 0;
int end = salaryArray.length - 1;
float cap = -1;
int m = -1;
while (begin <= end) {
m = (begin + end) / 2;
int amount = salaryTotalCap - salarySum[m - 1];
float possibleCap = amount / (salaryArray.length - m);
if (possibleCap < salaryArray[m-1]) {
end = m - 1;
}
if (possibleCap > salaryArray[m]) {
begin = m + 1;
}
if (possibleCap >= salaryArray[m-1] && possibleCap <= salaryArray[m]) {
cap = possibleCap;
break;
}
}
if (cap != -1) {
System.out.println("the capping position is :" + m);
}
return cap;
}
}
SalaryCap类用来实现上面所描述的算法,构造函数传入的数值salaries表示要查找截断点的原数组,capTotal对应的是算法描述中的值T,也就是新的总值。数组传入后,先对其进行排序,也就是执行Arrays.sort(this.salariesArray)。然后我们启动一个新数组salarySum用来统计数组元素的值的总和,例如salarySum[0] = salaryArra[0], salarySum[1] = salaryArray[0] + salaryArray[1], salarySum[2] = salaryArray[0] + salaryArray[1] + salaryArray[2], 依次类推。
函数getSalaryCap是对前面算法的实现。while循环就是在执行二分查找,代码先获取中点,也就是:
m = (begin + end) / 2;
接着用总值减去中点前所有元素之后,把剩余的值除以中点之后元素个数,得到截断值,然后判断截断值的属性。
if (possibleCap < salaryArray[m-1]) {
end = m - 1;
}
上面代码表示,如果截断值比截断点前面元素要小,那么截断点在当前元素的左边。
if (possibleCap > salaryArray[m]) {
begin = m + 1;
}
上面代码表示,如果截断值比截断点原来的值还要大,那表明截断点应该在当前元素的右边。
if (possibleCap >= salaryArray[m-1] && possibleCap <= salaryArray[m]) {
cap = possibleCap;
break;
}
上面代码表示,当前截断值既大于截断点前面元素的值,又比截断点原来的值要小,于是当前节点是合适的截断点,当前截断值也是合适的截断值。
我们再看看主函数的实现:
public static void main(String[] args) {
int size = 10;
int[] salaries = new int[size];
Random rand = new Random();
int capAmount = 0;
for (int i = 0; i < size; i++) {
salaries[i] = rand.nextInt(100) + 100;
}
Arrays.sort(salaries);
System.out.println("Array elements are: ");
for (int i = 0; i < size; i++) {
System.out.print(salaries[i] + " ");
}
int cappingPosition = rand.nextInt(size) + 1;
int capValue = (salaries[cappingPosition - 1] + salaries[cappingPosition]) / 2;
System.out.println("\ncapping position is:"+ cappingPosition +" cap value should is:" + capValue);
for (int i = 0; i < cappingPosition; i++) {
capAmount += salaries[i];
}
int count = (salaries.length - cappingPosition);
capAmount += count * capValue;
try {
SalaryCap sc = new SalaryCap(salaries, capAmount);
System.out.println("valid cap is : " + sc.getSalaryCap());
} catch (Exception e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
在主函数中,首先构造一个含有10个元素的数值,数值中元素是随机生成的,范围在100到200之间,然后先把数组排序,接着在数组10个元素中随机选取一个左截断点,把截断点和它前面元素值加在一起除以2作为截断值,然后计算出新的总值capValue, 把数组和新总值传入我们上面构造出的类,运行后,如果结果正确的话,SalaryCap返回的截断点和截断值应该和我们在main函数中构造的截断点和截断值是一模一样的。
上面代码运行后,结果如下:
Array elements are:
105 106 120 124 138 142 150 165 193 196
capping position is:4 cap value should is:131
the capping position is :4
valid cap is : 131.0
根据运行结果来看,算法找出的截断点和截断值跟我们预先设置的是一样的,于是我们算法的实现的正确的。由于截断点和截断值未必是唯一的,如果你多次运行程序,有可能发现结果给定的截断点和截断值可能不一样,但得到的结果还是可以满足条件的。
算法实现需要对数组进行排序,因此算法时间复杂度为O(lgn), 因为需要构建一个新数组来存储元素和,所以空间复杂度为O(n)。
详细的代码讲解和调试演示请参看视频:
如何进入google,算法面试技能全面提升指南
更多技术信息,包括操作系统,编译器,面试算法,机器学习,人工智能,请关照我的公众号: