Summary Ranges(228)
Given a sorted integer array without duplicates, return the summary of its ranges.
For example, given [0,1,2,4,5,7], return ["0->2","4->5","7"].
Credits:
Special thanks to @jianchao.li.fighter for adding this problem and creating all test cases.
public class Solution {
public List summaryRanges(int[] nums) {
List list=new ArrayList();
for(int i=0;i"+nums[i]);
}else{
list.add(a+"");
}
}
return list;
}
}
238.Product of Array Except Self
Given an array of n integers where n > 1, nums, return an array output such that output[i] is equal to the product of all the elements of nums except nums[i].
Solve it without division and in O(n).
For example, given [1,2,3,4], return [24,12,8,6].
Follow up:
Could you solve it with constant space complexity? (Note: The output array does not count as extra space for the purpose of space complexity analysis.)
Subscribe to see which companies asked this question.
Show Tags
Show Similar Problems
public class Solution {
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] res = new int[n];
res[0] = 1;
for (int i = 1; i < n; i++) {
res[i] = res[i - 1] * nums[i - 1];
}
int right = 1;
for (int i = n - 1; i >= 0; i--) {
res[i] *= right;
right *= nums[i];
}
return res;
}
}
思路:
最开始是想全部乘,然后除以自身。但是有0的话行不通。
上述解法是对于第i哥元素。先求 1 * arr[0] * … * arr[i-1];
然后再乘以arr[n-1] * ..arr[i+1];
268.Missing Number
Given an array containing n distinct numbers taken from 0, 1, 2, ..., n, find the one that is missing from the array.
For example,
Given nums = [0, 1, 3] return 2.
Note:
Your algorithm should run in linear runtime complexity. Could you implement it using only constant extra space complexity?
Credits:
Special thanks to @jianchao.li.fighter for adding this problem and creating all test cases.
Subscribe to see which companies asked this question.
思路 :
求和相见。差值就是缺少的数字。另外一种是异或。a^a=0.
public class Solution {
public int missingNumber(int[] nums) {
int sum=0;
int n=nums.length;
for(int i=0;i解法2
The basic idea is to use XOR operation. We all know that abb =a, which means two xor operations with the same number will eliminate the number and reveal the original number.
In this solution, I apply XOR operation to both the index and value of the array. In a complete array with no missing numbers, the index and value should be perfectly corresponding( nums[index] = index), so in a missing array, what left finally is the missing number.
public int missingNumber(int[] nums) {
int xor = 0, i = 0;
for (i = 0; i < nums.length; i++) {
xor = xor ^ i ^ nums[i];
}
return xor ^ i;
}
283.Move Zeroes
Given an array nums, write a function to move all 0's to the end of it while maintaining the relative order of the non-zero elements.
For example, given nums = [0, 1, 0, 3, 12], after calling your function, nums should be [1, 3, 12, 0, 0].
Note:
- You must do this in-place without making a copy of the array.
- Minimize the total number of operations.
Credits:
Special thanks to @jianchao.li.fighter for adding this problem and creating all test cases.
Subscribe to see which companies asked this question.
思路:尽可能少的移动,那就是一个元素最好只移动一次。将第一个非o的放在第一个位置,第二个非零的放在第二个位置,然后剩下的全部设为0.
public class Solution {
public void moveZeroes(int[] nums) {
if(nums.length==0 ||nums==null) return ;
int pos=0;
for(int num:nums){
if(num!=0){
nums[pos]=num;
pos++;
}
}
for(;pos287. Find the Duplicate Number
Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.
Note:
- You must not modify the array (assume the array is read only).
- You must use only constant, O(1) extra space.
- Your runtime complexity should be less than
O(n2). - There is only one duplicate number in the array, but it could be repeated more than once.
Credits:
Special thanks to @jianchao.li.fighter for adding this problem and creating all test cases.
Subscribe to see which companies asked this question.
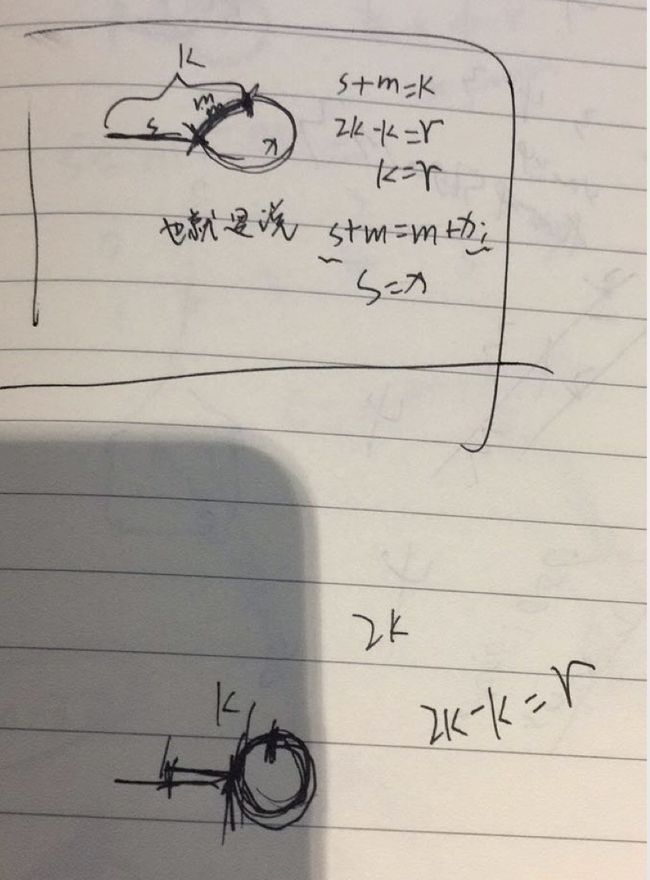
思路:类似于一个连表有环,求环的交叉点。
The main idea is the same with problem Linked List Cycle II,https://leetcode.com/problems/linked-list-cycle-ii/. Use two pointers the fast and the slow. The fast one goes forward two steps each time, while the slow one goes only step each time. They must meet the same item when slow==fast. In fact, they meet in a circle, the duplicate number must be the entry point of the circle when visiting the array from nums[0]. Next we just need to find the entry point. We use a point(we can use the fast one before) to visit form begining with one step each time, do the same job to slow. When fast==slow, they meet at the entry point of the circle. The easy understood code is as follows.
public class Solution {
public int findDuplicate(int[] nums) {
if(nums.length>1){
int slow=nums[0];
int fast=nums[nums[0]];
while(slow!=fast){
slow=nums[slow];
fast=nums[nums[fast]];
}
fast=0;
while(fast!=slow){
fast=nums[fast];
slow=nums[slow];
}
return slow;
}
return -1;
}
}