Validate Binary Search Tree
Method: Traverse and Divide and Conquer.
If it is a valid BST, use in-order traverse and get the a list. The list should be sorted unique increasing list.
Divide and conquer: Every time, remember the minvalue, maxvalue, and isBST. Check the min, max value after the check of isBST.
Learned:
At first, I did it in a wrong way. I just compared the root value with left node value and right node value. Here is the counter example. {2, 3, 4, 1, 5, #,#}
Binary Tree Non-recursive Traversal
Pre-order Solution:
In-order Solution:
With Recursion: Inorder, Left, root, right. Without Recursion: Use the stack. Always left
Post-order Solution:
Using Visited Flags: We will meet the root node for twice. For the first time, we need to remember we have already visited it and turn to its right node. If we meet the root node for twice, we need to push it into the result list. Here is my python code.
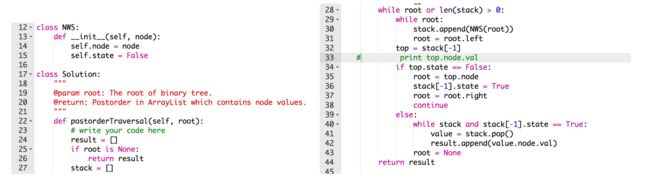
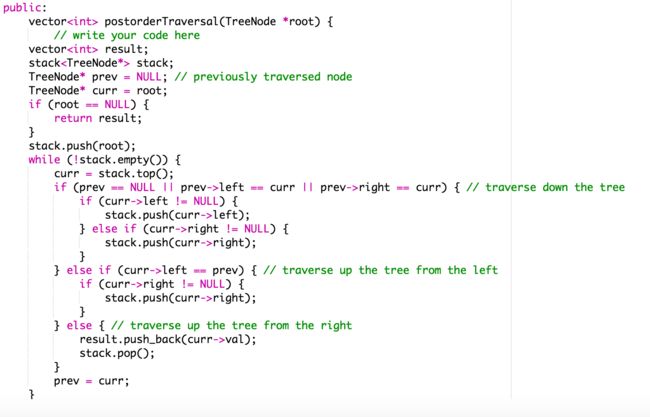
One Stacks Methods: Source
We use a prev variable to keep track of the previously-traversed node. Let’s assume curr is the current node that’s on top of the stack. When prev is curr' s parent, we are traversing down the tree. In this case, we try to traverse to curr' s left child if available (ie, push left child to the stack). If it is not available, we look at curr' s right child. If both left and right child do not exist (ie,curr is a leaf node), we print curr' s value and pop it off the stack. If prev is curr' s left child, we are traversing up the tree from the left. We look at curr' s right child. If it is available, then traverse down the right child (ie, push right child to the stack), otherwise print curr' s value and pop it off the stack. If prev is curr' s right child, we are traversing up the tree from the right. In this case, we print curr' s value and pop it off the stack.
Two Stacks Method: We need to reverse the result and publish it. The order of post-order is left , right , root. So we want the reverse of post-order. So it is root, right, left. So we first visit the root, then the right, then the left. Here is the code.
Printing a Binary Tree in Level Order
BFS: Using Queue. DFS: O(n), Stack We need remember the level when we push the node into the stack. Just construct a type
Printing a Binary Tree in Zig-Zag Level Order
BFS: Use the bool variable to record the order from left to right. DFS: Insert with level and according to even or odd.
Populating Next Right Pointers in Each Node I & II
It is easy to think of solutions for the first problem. How about the hard one? It has extra requirement: You may only use constant extra space. In such a case, we could iteratively visit the node level by level and use a needle to link them.
Finding the Maximum Height of a Binary Tree
It is quite easy to use DFS recursive method to solve this problem. The hard one is to write non-recursive method. We can use BSF method. Level by level and use a counter variable to remember how many level have we visited.
Serialization/Deserialization of Binary Tree
We can use pre-order to solve this problem. Use "#" for the NULL representation
Rebuild Binary Search Tree from Pre-order Traversal, Construct Binary Tree from Preorder and Inorder Traversal, from Inorder and Postorder Traversal.
I. This is to build BST. The difference between Binary Search Tree and Binary Tree is a binary tree where the left child contains only nodes with values less than the parent node, and where the right child only contains nodes with values greater than or equal to the parent. We pre-order is enough for us to construct tree. Method One(O(n*n)): find the index of first element which is greater than root which is the head of preorder list. Method Two(O(n)): The trick is to set a range {min .. max} for every node. Initialize the range as {INT_MIN .. INT_MAX}. The first node will definitely be in range, so create root node. To construct the left subtree, set the range as {INT_MIN …root->data}. If a values is in the range {INT_MIN .. root->data}, the values is part part of left subtree. To construct the right subtree, set the range as {root->data..max .. INT_MAX}. Method Tree(O(n)): Using a stack based on iterative solution.
II. Always remember pre-order list[0] will remember the root of current tree. Use recursive method to construct the tree.
III. I really like the neat code on LeetCode. Same idea from II.
Print Edge Nodes (Boundary) of a Binary Tree
Print the left edge if it is not the leaf from top to the bottom, Print the leaf, Print the right edge if it is not the leaf from bottom to the top.
Convert Binary Search Tree to Doubly Linked List
It is actually a change of in-order non-recursive iteration.
Lowest Common Ancestor of a Binary Tree
Recursive:
Iterative: Find the ancestors of p and q. Compare the ancestors and you can find the lowest common ancestor. We need to find a way from root to p and to q.
Complete Binary Tree
Method1: Use bfs to visit every node. When it meet the NULL and stops. If it continue to visit the leaf and find a non-null leaf, return false.
Method2: First calculate the left edge depth. Then check the depth of last level. All nodes in the last level are as far left as possible. We need to check depth, isDecremented,