前言:进入数据库的理论部分,非常抽象...
数据库在我看来有三个阶段的学习:
- 学会增删改查
- 学会设计并优化数据库
- 了解并实现一个简单的数据库
我正在处于第二阶段的学习,这一部分十分抽象,多过几遍就好了。打好基础才能走得远,加油
设计数据库有很多原则要遵循,第一范式是所有范式中最基础的部分
第一范式(1NF)
原子性这个概念在计算机中非常普遍,简单说就是不可分割。第一范式的意思就是:关系模式 R 的所有属性都是原子的
属性原子性的通常相对与如何使用这一属性来说的
比如:「姓名」这一属性,如果我们在使用的时候不把它拆分成姓和名,那么这就是原子的
处理非原子值有两种方法:
- 对于组合属性:让每个子属性成为一个属性
- 对于多值属性:为多的属性创建一条新的记录(元组)
像我这样的新手设计出来的数据库肯定有各种各样的冗余,所以对我来说的第一步就是学会模式分解
模式分解理论——函数依赖
在开始学会模式分解之前我们得先学会一些理论是什么:
函数依赖(function dependencies)
多值依赖(multivalued dependencies)等我学会了再说
什么是函数依赖
简单说两个属性 A B,如果 A 确定了,B 也确定了。
符号记做:。A 是 B 的依赖,A 决定 B
函数依赖的使用
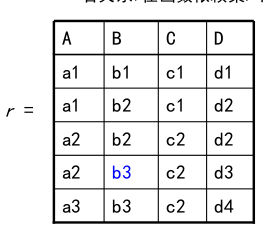
假设我们有这么一个表:
有这样的函数依赖:
F = {
A ➜ C,
AB ➜ D,
ABC ➜ D
}
这个依赖的意思就是有了 A 属性就能推出 C 属性,有 AB 属性就能确定 D 属性,有 ABC 属性就能确定 D(这一条很奇怪,好像多余了,这是一个问题,放在后面解答)
被所有关系实例都满足的函数依赖称为平凡的:
比如:A ➜ A,AB ➜ A
一般的:有两个属性的集合 ,如果 ,那么 就是平凡的函数依赖。反之,如果 但是 就是一个非凡的函数依赖
依赖函数的另一个概念——闭包
这里有一个抽象的定义:被 F 逻辑蕴含的全体依赖函数的集合就是 F 的闭包
举个例子:
假如有这么一个依赖:
F = { A ➜ B, B ➜ C }
那么 F 的闭包()就是
A ➜ B,
A ➜ C,
AB ➜ A,
AB ➜ B,
...
ABC ➜ ABC
依赖函数中的公理——Armstrong 公理
你可能对上面的运算有那么一点点陌生:在这里我将列出 3 种公理,以及 3 种补充定律
这上面的六个公式是完全正确的。现在我们用这个 6 个公式搞事情。
- 计算
FC = F
do {
for each f in FC:
对 f 使用自反律和增补律
保存结果
将所有保存的结果放入 FC 中
// 对在 FC 中的每一对 f1, f2
for each f1, f2 in FC
if f1 和 f2可以使用传递律结合起来
保存结果
将所有保存的结果放入 FC 中
}while(FC 不再变化)
-
计算属性集合 是否是超码
计算 的闭包看表的所有属性是否在其中
数据库的合理更新——函数依赖
在数据库更新的时候会检查是否满足当前表的函数依赖,如果依赖太多计算量太大,而且依赖中也可能重现冗余的情况。
使用「正则覆盖」检查数据库的更新。
通俗说:「正则覆盖」就是最小化的函数依赖,举个栗子
有这样的函数依赖
F = {
A ➜ C,
A ➜ B,
B ➜ C
}
其中 A ➜ C 就是冗余的得到简化的依赖函数
F = {
A ➜ B,
B ➜ C
}
这个过程就是「正则覆盖」
用伪代码详细叙述这个算法:
do {
首先使用合并规则更新 F
再找出无关属性并从 F 中剔除
}while(F 不再变化)
模式分解
学习了以上函数依赖的前置知识以后,我们可以来做一些模式分解了。向着更好的数据库发展!
对于模式分解要做到:
原模式(R)的所有属性必须出现在分解后的(R1,R2)中
-
无损连接分解
分解后的二个子模式的共同属性必须是 R1 或 R2 的码,投影属性并自然连接后还和原来关系相同
-
保持依赖
有效地检查更新操作(以确保没有违反任何依赖函数)
-
没有冗余
最好满足 BCNF 或 3NF(BCNF 和 3NF 以后再说)
举个例子
R = ( A, B, C ) , F = { A ➜ B, B ➜ C },有两种分解方式
第一种方式: R1 = ( A, B ) 和 R2 = ( B, C )
分析如下:
- 共同属性是 B,且 B ➜ C 所以是无损连接分解
- 第一张表是 A ➜ B,第二张表是 B ➜ C,保持依赖
第二种方式: R1 = ( A, B ) 和 R2 = ( A, C )
- 共同属性是 A,由于推得 A ➜ C。所以是无损连接分解
- 由于两张表是 A ➜ B,A ➜ C。与原来不同,所以没有保持依赖