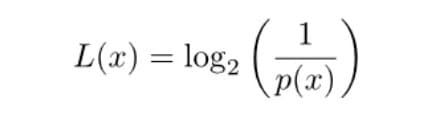所谓悲剧的人生,并不仅仅在于被不幸击中,更在于这种不幸的不可避免
提到压缩,不得不提的概念就是“熵”,“熵”(entropy)是香农创立的信息论中最核心的概念,代表了一个系统的内在的混乱程度。香农本来打算用“不确定性”(uncertainty)来表达这个概念,当他和冯·诺伊曼讨论这个问题时,冯·诺伊曼对香农建议说:“你应该把它称之为‘熵’“。“熵”这个经典的概念,跨越了信息论、物理学、数学、生态学、社会学等领域,至今仍在人工智能领域给人带来新的启迪。
香农给出了一个数学公式。L表示所需要的二进制位,p(x)表示发生的概率。通过公式,可以计算出某种概率的结果所需要的二进制位。
知道了每种概率对应的编码长度,就可以计算出一种概率分布的平均编码长度。
H,就是该种概率分布的平均编码长度。理论上,这也是最优编码长度,不可能获得比它更短的编码了。
前面公式里的H(平均编码长度),其实就是信息量的度量。H越大,表示需要的二进制位越多,即可能发生的结果越多,不确定性越高。
比如,H为1,表示只需要一个二进制位,就能表示所有可能性,那就只可能有两种结果。如果H为6,六个二进制位表示有64种可能性,不确定性大大提高。
信息论借鉴了物理学,将H称为"信息熵"(information entropy)。在物理学里,熵表示无序,越无序的状态,熵越高。
很显然,不均匀分布时,某个词出现的概率越高,编码长度就会越短。
从信息的角度看,如果信息内容存在大量冗余,重复内容越多,可以压缩的余地就越大。日常生活的经验也是如此,一篇文章翻来覆去都是讲同样的内容,摘要就会很短。反倒是,每句话意思都不一样的文章,很难提炼出摘要。
图片也是如此,单调的图片有好的压缩效果,细节丰富的图片很难压缩。
由于信息量的多少与概率分布相关,所以在信息论里面,信息被定义成不确定性的相关概念:概率分布越分散,不确定性越高,信息量越大;反之,信息量越小。
压缩
压缩的原理是把文件的二进制代码压缩,把相邻的0,1代码减少,比如有000000,可以把它变成6个0 的写法60,来减少该文件的空间。
压缩文件的基本原理是查找文件内的重复字节,并建立一个相同字节的"词典"文件,并用一个代码表示,比如在文件里有几处有一个相同的词"中华人民共和国"用一个代码表示并写入"词典"文件,这样就可以达到缩小文件的目的。
由于计算机处理的信息是以二进制数的形式表示的,因此压缩软件就是把二进制信息中相同的字符串以特殊字符标记来达到压缩的目的。
其实,所有的计算机文件归根结底都是以“1”和“0”的形式存储的,只要通过合理的数学计算公式,文件的体积都能够被大大压缩以达到“数据无损稠密”的效果。总的来说,压缩可以分为有损和无损压缩两种。如果丢失个别的数据不会造成太大的影响,这时忽略它们是个好主意,这就是有损压缩。有损压缩广泛应用于动画、声音和图像文件中,典型的代表就是影碟文件格式mpeg、音乐文件格式mp3和图像文件格式jpg。但是更多情况下压缩数据必须准确无误,人们便设计出了无损压缩格式,比如常见的zip、rar等。
有两种形式的重复存在于计算机数据中,一种是短语形式的重复,即三个字节以上的重复,对于这种重复,zip用两个数字:1.重复位置距当前压缩位置的距离;2.重复的长度,来表示这个重复,假设这两个数字各占一个字节,于是数据便得到了压缩。
第二种重复为单字节的重复,一个字节只有256种可能的取值,所以这种重复是必然的。其中,某些字节出现次数可能较多,另一些则较少,在统计上有分布不均匀的倾向,这是容易理解的,比如一个 ASCII 文本文件中,某些符号可能很少用到,而字母和数字则使用较多,各字母的使用频率也是不一样的,据说字母 e 的使用概率最高;许多图片呈现深色调或浅色调,深色(或浅色)的像素使用较多(这里顺便提一下:png 图片格式是一种无损压缩,其核心算法就是 zip 算法,它和 zip 格式的文件的主要区别在于:作为一种图片格式,它在文件头处存放了图片的大小、使用的颜色数等信息)。这样,就有了压缩的可能:给 256 种字节取值重新编码,使出现较多的字节使用较短的编码,出现较少的字节使用较长的编码,这样一来,变短的字节相对于变长的字节更多,文件的总长度就会减少,并且,字节使用比例越不均匀,压缩比例就越大。
几种压缩算法
RLE
RLE 又叫 Run Length Encoding ,是一个针对无损压缩的非常简单的算法。它用重复字节和重复的次数来简单描述来代替重复的字节。尽管简单并且对于通常的压缩非常低效,但它有的时候却非常有用(例如, JPEG 就使用它)。
RLE 解码器遇到符号‘ 0 ’ 的时候,它表明后面的两个字节决定了需要输出哪个符号以及输出多少次。
RLE 可以使用很多不同的方法。基本压缩库中详细实现的方式是非常有效的一个。一个特殊的标记字节用来指示重复节的开始,而不是对于重复非重复节都 coding run 。为了最优化效率,标记字节应该是输入流中最少出现的符号(或许就不存在)。
哈夫曼
哈夫曼编码(Huffman Coding)也称为“赫夫曼编码”,是David A. Huffman 1952年发明的一种构建极小多余编码的方法。
在计算机数据处理中,霍夫曼编码使用变长编码表对源符号进行编码,出现频率较高的源符号采用较短的编码,出现频率较低的符号采用较长的编码,使编码之后的字符串字符串的平均长度 、期望值降低,以达到无损压缩数据的目的。
源字符编码的长短取决于其出现的频率,我们把源字符出现的频率定义为该字符的权值。由此生成哈夫曼树,又称为最优二叉树。是一种带权路径长度最短的二叉树。
假设有n个权值{w1,w2,w3,w4...,wn},构造一棵有n个节点的二叉树,若树的带权路径最小,则这颗树称作哈夫曼树。
通过树分析,出现频率越高的字母(也即权值越大),其编码越短。这便使编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。
这个实现的基本缺陷是:
1. 慢位流实现
2. 相当慢的解码(比编码慢)
3. 最大的树深度是 32 (编码器在任何超过 32 位大小的时候退出)
哈夫曼编码在数据有噪音的情况(不是有规律的,例如 RLE )下非常好,这中情况下大多数基于字典方式的编码器都有问题。
Rice
对于由大 word (例如: 16 或 32 位)组成的数据和教低的数据值, Rice 编码能够获得较好的压缩比。音频和高动态变化的图像都是这种类型的数据,它们被某种预言预处理过(例如 delta 相邻的采样)。
尽管哈夫曼编码处理这种数据是最优的,却由于几个原因而不适合处理这种数据(例如: 32 位大小要求 16GB 的柱状图缓冲区来进行哈夫曼树编码)。因此一个比较动态的方式更适合由大 word 组成的数据。
Rice 编码背后的基本思想是尽可能的用较少的位来存储多个字(正像使用哈夫曼编码一样)。实际上,有人可能想到 Rice 是静态的哈夫曼编码(例如,编码不是由实际数据内容的统计信息决定,而是由小的值比高的值常见的假定决定)。
编码非常简单:将值 X 用 X 个‘ 1 ’位之后跟一个 0 位来表示。
Lempel-Ziv (LZ77)
Lempel-Ziv 压缩模式有许多不同的变量。基本压缩库有清晰的 LZ77 算法的实现( Lempel-Ziv , 1977 ),执行的很好,源代码也非常容易理解。
LZ 编码器能用来通用目标的压缩,特别对于文本执行的很好。它也在 RLE 和哈夫曼编码器( RLE , LZ ,哈夫曼)中使用来大多数情况下获得更多的压缩。
简单的讲, LZ 算法被认为是字符串匹配的算法。例如:在一段文本中某字符串经常出现,并且可以通过前面文本中出现的字符串指针来表示。当然这个想法的前提是指针应该比字符串本身要短。
例如,在上一段短语“字符串”经常出现,可以将除第一个字符串之外的所有用第一个字符串引用来表示从而节省一些空间。
一个字符串引用通过下面的方式来表示:
1. 唯一的标记
2. 偏移数量
3. 字符串长度
由编码的模式决定引用是一个固定的或变动的长度。后面的情况经常是首选,因为它允许编码器用引用的大小来交换字符串的大小(例如,如果字符串相当长,增加引用的长度可能是值得的)。
使用 LZ77 的一个问题是由于算法需要字符串匹配,对于每个输入流的单个字节,每个流中此字节前面的哪个字节都必须被作为字符串的开始从而尽可能的进行字符串匹配。基本压缩库使用一个清晰的实现来保证所有的符号和引用是字节对齐的,因此牺牲了压缩比率,并且字符串匹配程序并不是最优化的(没有缓存、历史缓冲区或提高速度的小技巧),这意味着算法非常慢。
另一个问题是为了最优化压缩而调整字符串引用的表示形式并不容易。例如,必须决定是否所有的引用和非压缩字节应该在压缩流中的字节边界发生。