数据清洗
删除重复
数据-标记重复个案-把需要参考的都拖入右边定义-生成0代表重复,1代表不重复-在01这一列右键升序-删除0
数据抽取
字段拆分(例如身份证号提取生日)
转换-计算变量-函数选择字符串-函数选择Substr(3)-更改参数substr(字符串(身份证),从第几个开始提取,提取几个)-目标变量改名字-类型改为字符串
随机抽样
数据-选择个案-随机个案样本-大约&(可选择把选定个案复制到新数据集)
数据合并
年月日字段合并
转换-计算变量-字符串-函数选择Concat(年份,”-“,月份,”-”日)必须英文标点-字符串宽度为10
若想进行计算,可在变量视图中将数据类型改为日期型yyyy/mm/dd
记录合并
将两个表中的数据合并,不用复制粘贴
打开一个表-数据-合并文件-添加个案-从外部选
数据分组
可视分箱(数据分段)
转换-可视化分箱-将要分的数据拖到右边-填写分箱化变量-生成分割点-生成标签
逆推的话,则采用 转换-重新编码为不同变量-旧值和新值
数据标准化
0-1标准化
转换-计算变量-目标变量写标准化值-公式(x-min)(max-min)-目标变量数值
Z标准化
分析-描述统计-描述-变量拖动
描述性分析
频率分析
分析-描述统计-频率-(Q几可以右键显示)-拖入
百分比:每类别有效值和缺省值所占总体比例
有效百分比:有效值所占
累计百分比:从第一个类别依次累加
连续变量频率
分析-描述统计-频率-拖入-statistics-四位分数平均值百分点离散程度等选选选-图表选择
条形图:数据分布,长度表示频数
直方图:连续数据,面积表示频数
饼图:数据结构
交叉表分析
分析-描述统计-交叉表-行列以此拖入-单元格
多选题定义
分析-表-多重定制-选择要弄得题目拖-二分法(计数值1)或类别-添加-更改集合名(Q几)和集合标签(Q几.名称)
报表
分析-定职表-同时选中左侧要选的-拖入行or列-摘要统计加权数
自定义分组
分析-定制表-拖入-分类和总计-选中起止点的标签-添加小计
相关分析
皮尔逊相关系数r反映连续变量之间线性相关强度的度量指标 【-1,1】为0则线性无关,绝对值小于0.3低度相关,高于0.8高度相关。正负号表示正or负相关
回归分析
简单线性回归
步骤:1.确定自变量和因变量
2.绘制散点图,看r:
图形-旧对话框-散点图-简单散点-将需要比较的变量拖入xy轴分析-相关-双变量-依次
入,选择皮尔逊-输出表格看r的大小确立相关度
3.估计模型参数,建立线性回归模型
分析-回归-线性,拖入自变因变-统计和选项一般保留默认值
4.对回归模型进行检验
输出了四个表:
1线性回归模型输入/除去表
2线性模型回归模型汇总表:R2越接近1,拟合效果越好
3线性回归方差分析表:一般看F和显著性P,P若大于0.05则不具有显著地统计学意义,0.01-0.05具有显著的统计学意义,若小于0.01极其显著
4.线性回归模型回归系数表:一般根据B里面的两个数可以列出Y=A+Bx的式子
5.利用回归模型进行预测:根据式子代入,可在保存中勾选预测值中的未标准化
多重线性回归(多个自变量)
步骤如上,图形-旧对话框-散点图-矩阵散点图-定义-拖入要比较的多个变量到矩阵变量
自动线性建模
连续变量,分类变量,均可作为自变量参与建模
自动建模
分析-回归-自动建模-预测变量中是可以编辑的,将明显不是自变量的移到“字段”中(例如日期,用户id)将因变量移到“目标”中-运行
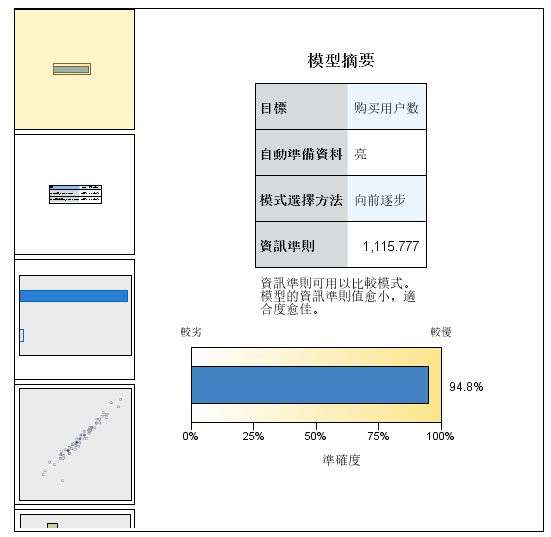
结果解读
以图示为例,其中左侧图都可以双击查看
Logistic回归
因变量是分类变量的回归,对数变换,分类变量分为二分类(是or否)和多分类。二分类就是logistic回归,1和0 对应 是和否 概率中P>0.5 对应的是1
分析-回归-二元logistic-移动因变量和协变量-保存-勾选概率值
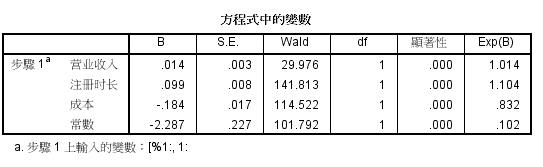
输出的表格重点关注
此表格中,未续约数是300 续约数是797 续约判断准确性73.1%
回归检验量为 瓦尔德(wald)显著性全部小于0.01 极显著
logit(P)=-2.287+0.014*营业收入+0.099*注册时长-0.184*成本
预测
在上述“保存”中-将模型信息导出到XML文件-再打开一个类似的新文件(因变量自变量相同)-实用程序-评分向导-找到保存的文件-勾选预测值
时间序列分析
用于预测的时间序列,假设事物发展延伸到未来,具有不规则性,不考虑因果关系
一般会把季节变动因素分解出去(因为季节变动会让预测模型变为不规则)
定义日期指示变量
即便是数据中有“日期”这个变量,也要重新定义指示变量
数据-定义日期和时间-左侧个案根据变量起止来决定,例如年份,月份-年份输入
序列发展趋势
分析-预测-序列图-移动变量-date作为时间轴标签
序列图中,季节波动大后续采用乘法模型(四种因素相互影响)Y=T(长期模型)*S(季节变动)*C(循环变动)*I(不规则变动)
季节波动小采用加法模型 Y=T+S+C+I
例如下图 波动大 采用乘法
季节因素分离
分析-预测-季节性(周期性)分解-变量移动,选择模型
探索性分析
从大量的数据中发现未知有价值信息(找高端客户)
RFM分析(Recency交易时间间隔 Frequency交易次数 Monetary交易金额)
根据客户活跃度和交易金额贡献细分的方法
数据格式:1交易数据:每次交易占用一行,关键变量为客户ID,交易日期和交易金额
2客户数据:每个客户占用一行,关键变量是客户ID,交易总金额,交易总次数和最 近交易日期
直销-选择技术-帮助确定我的最佳联系人-交易数据-移动对应变量-输出可全部勾选-出现分析图
分析-描述统计-描述-将各种得分移动-转换-重新编码为不同变量-每次移动一个得分-
旧值和新值-从值到最高-框中输入平均值-右侧值中输入表示高的值-添加
旧值和新值-所有其他值-值中输入表示低的值-添加
数据-定义变量属性-找到之前改的分类拖入
聚类分析
让同一个类别的个体之间具有较高相似度,不同的则差别大
1.快速聚类分析(K均值聚类分析)
分析-分类-k平均值聚类-各种评定依据作为变量,个案选择每个人-共分为几组-保存勾选聚类成员
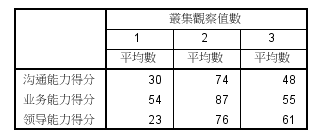
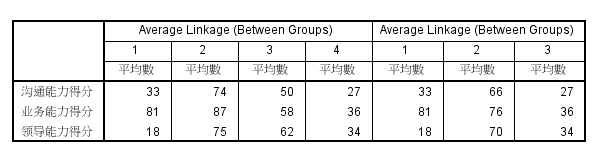
生成表后 分析-定制表(QCL移动到列 评判依据到行)
2.系统聚类分析
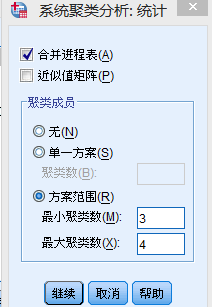
分析-分类-系统聚类-评判依据移入变量
统计-可输入生成类别范围(例如3-4)
图-谱系图(即树状图)
方法-(默认组间连接 平方欧式距离)可勾选Z得分
保存-可勾选解的范围(如果之前勾选范围的话)
分析-描述统计-频率
分析-定制表(将CLU移动到列 评判依据到行)
3.二阶聚类分析
分析-分类-两步聚类-评判依据为连续变量-性别学历等为分类变量-输出选择透视表和创建聚类成员变量
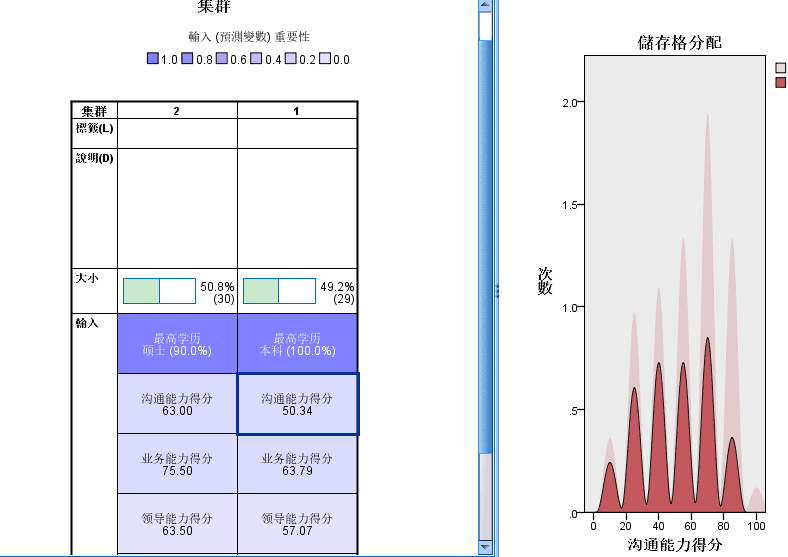
对比表格BCI变化量等三项依据,选择最大的,则为最佳类别数
双击最后一张图表,可模型查看器,按ctrl点击分类可以对比单元格分布
因子分析
通过研究变量间的相关系数矩阵,把复杂关系归结成少数几个综合因子 降维
连续变量,各按个数为变量个数5倍以上,KMO在0.5以上(0.8以上极其适合)
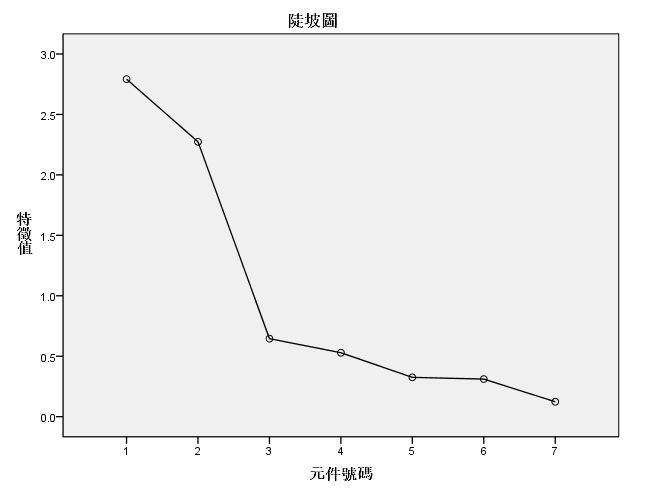
分析-降维-因子分析-移动变量-描述(原始结果和KMO球状度)-抽取(默认以及碎石图)-旋转(最大方差法)-得分(保存为变量 回归)-选项(按大小排序,取消小系数,最后数值限定输出)
在分析时
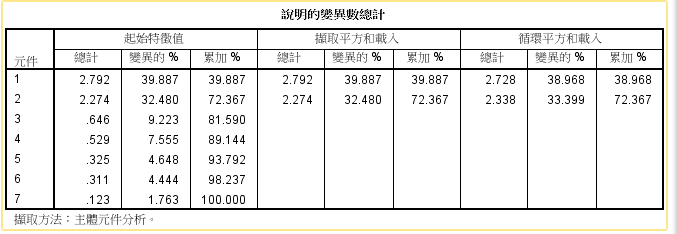
提取的因子个数应该:下表第二列大于1(初始值) 第四列(累加)达到60,图上位置较陡
旋转载荷平方和(1,2,累加)
表中会呈现FAC1_1.FAC2_1.计算时,转换-计算变量-公式输入38.968/72.367*FAC1_1+33.399/72.367*FAC2_1 最后综合得分排序即可
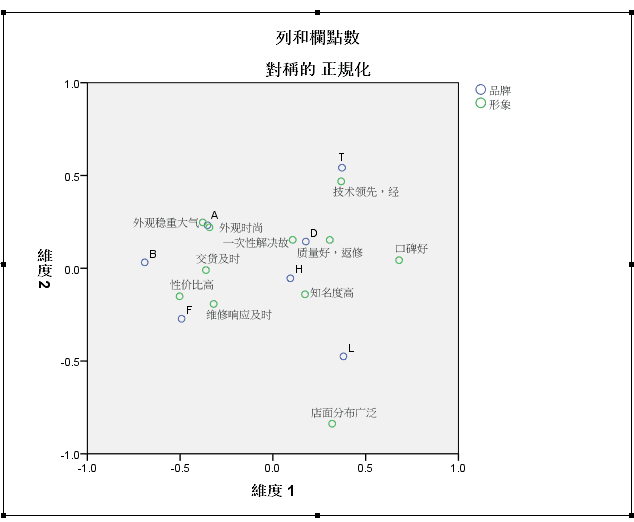
对应分析
和图形有关,分类变量构成的交叉表
数据-加权个案-数值为频率变量
分析-降维-对应分析-移动
下表 同一变量类别距离越近,差异越小
不同类别距离越近,相关性越大