转-推荐算法中的矩阵分解

一、推荐算法概述

对于推荐系统(Recommend System, RS)，从广义上的理解为：为用户(User)推荐相关的商品(Items)。常用的推荐算法主要有：

• 基于内容的推荐(Content-Based Recommendation)
• 协同过滤的推荐(Collaborative Filtering Recommendation)
• 基于关联规则的推荐(Association Rule-Based Recommendation)
• 基于效用的推荐(Utility-Based Recommendation)
• 基于知识的推荐(Knowledge-Based Recommendation)
• 组合推荐(Hybrid Recommendation)

在推荐系统中，最重要的数据是用户对商品的打分数据，数据形式如下所示：

这里写图片描述

其中，U1⋯U5表示的是5个不同的用户，D1⋯D4表示的是4个不同的商品，这样便构成了用户-商品矩阵，在该矩阵中，有用户对每一件商品的打分，其中“-”表示的是用户未对该商品进行打分。

在推荐系统中有一类问题是对未打分的商品进行评分的预测。

二、基于矩阵分解的推荐算法

2.1、矩阵分解的一般形式

矩阵分解是指将一个矩阵分解成两个或者多个矩阵的乘积。对于上述的用户-商品矩阵(评分矩阵)，记为Rm×n。可以将其分解成两个或者多个矩阵的乘积，假设分解成两个矩阵Pm×k和Qk×n，我们要使得矩阵Pm×k和Qk×n的乘积能够还原原始的矩阵Rm×n：

Rm×n≈Pm×k×Qk×n=R^m×n

其中，矩阵Pm×k表示的是m个用户与k个主题之间的关系，而矩阵Qk×n表示的是k个主题与n个商品之间的关系。

2.2、利用矩阵分解进行预测

在上述的矩阵分解的过程中，将原始的评分矩阵Rm×n分解成两个矩阵Pm×k和Qk×n的乘积：

Rm×n≈Pm×k×Qk×n=R^m×n

那么接下来的问题是如何求解矩阵Pm×k和Qk×n的每一个元素，可以将这个问题转化成机器学习中的回归问题进行求解。

2.2.1、损失函数

可以使用原始的评分矩阵Rm×n与重新构建的评分矩阵R^m×n之间的误差的平方作为损失函数，即：

e2i,j=(ri,j−r^i,j)2=(ri,j−∑k=1Kpi,kqk,j)2

最终，需要求解所有的非“-”项的损失之和的最小值：

minloss=∑ri,j≠−e2i,j

2.2.2、损失函数的求解

对于上述的平方损失函数，可以通过梯度下降法求解，梯度下降法的核心步骤是

• 求解损失函数的负梯度：

∂∂pi,ke2i,j=−2(ri,j−∑k=1Kpi,kqk,j)qk,j=−2ei,jqk,j

∂∂qk,je2i,j=−2(ri,j−∑k=1Kpi,kqk,j)pi,k=−2ei,jpi,k

• 根据负梯度的方向更新变量：

pi,k′=pi,k−α∂∂pi,ke2i,j=pi,k+2αei,jqk,j

qk,j′=qk,j−α∂∂qk,je2i,j=qk,j+2αei,jpi,k

通过迭代，直到算法最终收敛。

2.2.3、加入正则项的损失函数即求解方法

通常在求解的过程中，为了能够有较好的泛化能力，会在损失函数中加入正则项，以对参数进行约束，加入L2正则的损失函数为：

E2i,j=(ri,j−∑k=1Kpi,kqk,j)2+β2∑k=1K(p2i,k+q2k,j)

利用梯度下降法的求解过程为：

• 求解损失函数的负梯度：

∂∂pi,kE2i,j=−2(ri,j−∑k=1Kpi,kqk,j)qk,j+βpi,k=−2ei,jqk,j+βpi,k

∂∂qk,jE2i,j=−2(ri,j−∑k=1Kpi,kqk,j)pi,k+βqk,j=−2ei,jpi,k+βqk,j

• 根据负梯度的方向更新变量：

pi,k′=pi,k−α(∂∂pi,ke2i,j+βpi,k)=pi,k+α(2ei,jqk,j−βpi,k)

qk,j′=qk,j−α(∂∂qk,je2i,j+βqk,j)=qk,j+α(2ei,jpi,k−βqk,j)

通过迭代，直到算法最终收敛。

2.2.4、预测

利用上述的过程，我们可以得到矩阵Pm×k和Qk×n，这样便可以为用户i对商品j进行打分：

∑k=1Kpi,kqk,j

2.3、程序实现

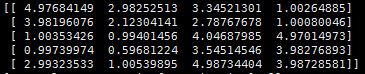
对于上述的评分矩阵，通过矩阵分解的方法对其未打分项进行预测，最终的结果为：

这里写图片描述

程序代码如下：

#!/bin/python
'''
Date:20160411
@author: zhaozhiyong
'''
from numpy import *

def load_data(path):
    f = open(path)
    data = []
    for line in f.readlines():
        arr = []
        lines = line.strip().split("\t")
        for x in lines:
            if x != "-":
                arr.append(float(x))
            else:
                arr.append(float(0))
        #print arr
        data.append(arr)
    #print data
    return data

def gradAscent(data, K):
    dataMat = mat(data)
    print dataMat
    m, n = shape(dataMat)
    p = mat(random.random((m, K)))
    q = mat(random.random((K, n)))

    alpha = 0.0002
    beta = 0.02
    maxCycles = 10000

    for step in xrange(maxCycles):
        for i in xrange(m):
            for j in xrange(n):
                if dataMat[i,j] > 0:
                    #print dataMat[i,j]
                    error = dataMat[i,j]
                    for k in xrange(K):
                        error = error - p[i,k]*q[k,j]
                    for k in xrange(K):
                        p[i,k] = p[i,k] + alpha * (2 * error * q[k,j] - beta * p[i,k])
                        q[k,j] = q[k,j] + alpha * (2 * error * p[i,k] - beta * q[k,j])

        loss = 0.0
        for i in xrange(m):
            for j in xrange(n):
                if dataMat[i,j] > 0:
                    error = 0.0
                    for k in xrange(K):
                        error = error + p[i,k]*q[k,j]
                    loss = (dataMat[i,j] - error) * (dataMat[i,j] - error)
                    for k in xrange(K):
                        loss = loss + beta * (p[i,k] * p[i,k] + q[k,j] * q[k,j]) / 2

        if loss < 0.001:
            break
        #print step
        if step % 1000 == 0:
            print loss

    return p, q

if __name__ == "__main__":
    dataMatrix = load_data("./data")

    p, q = gradAscent(dataMatrix, 5)
    '''
    p = mat(ones((4,10)))
    print p
    q = mat(ones((10,5)))
    '''
    result = p * q
    #print p
    #print q

    print result

其中，利用梯度下降法进行矩阵分解的过程中的收敛曲线如下所示：

这里写图片描述

'''
Date:20160411
@author: zhaozhiyong
'''

from pylab import *
from numpy import *

data = []

f = open("result")
for line in f.readlines():
    lines = line.strip()
    data.append(lines)

n = len(data)
x = range(n)
plot(x, data, color='r',linewidth=3)
plt.title('Convergence curve')
plt.xlabel('generation')
plt.ylabel('loss')
show()

参考文献

• 《大数据智能》
• Matrix Factorization: A Simple Tutorial and Implementation in Python