SciPy的optimize模块提供了许多数值优化的算法,一些经典的优化算法包括线性回归、函数极值和根的求解以及确定两函数交点的坐标等。下面首先介绍简单的线性回归模型,然后逐渐深入解决非线性数据拟合问题。
4.3.1拟合 curve_fit()函数
线性回归有许多拟合数据的方法,我们将使用curve_fit()函数,它利用的是最小二乘算法。最小二乘算法是一种数学优化技术,在机器学习领域最有名和有效的算法之一。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
以下示例中,我们首先从已知函数中生成一些带有噪声的数据,然后使用curve_fit()函数拟合这些噪声数据。示例中的已知函数我们使用一个简单的线性方程式,即f(x)=ax+b。示例代码:
import numpy as np
from scipy.optimize import curve_fit
#创建函数模型用来生成数据
def func(x, a, b):
return a*x + b
#生成干净数据
x = np.linspace(0, 10, 100)
y = func(x, 1, 2)
#对原始数据添加噪声
yn = y + 0.9 * np.random.normal(size=len(x))
#使用curve_fit函数拟合噪声数据
popt, pcov = curve_fit(func, x, yn)
#输出给定函数模型func的最优参数
print(popt)
返回结果如下:
[ 0.99734363 1.96064258]
如果有一个很好的拟合效果,popt返回的是给定模型的最优参数。我们可以使用pcov的值检测拟合的质量,其对角线元素值代表着每个参数的方差。
>>>print(pcov)
[[ 0.00105056 -0.00525282]
[-0.00525282 0.03519569]]
通过以下代码绘制出了拟合曲线与实际曲线的差异,示例代码:
m = np.array([x,np.ones(len(x))])
import pylab as pl
pl.plot(x, y, color="green",label = "actual data")
pl.plot(x, yn, "o", label = "actual data with noise")
pl.plot(x, np.dot(m.T,popt), color="yellow", label = "fitting data")
pl.legend(loc = "best")
pl.show()
下面做进一步研究,我们可以通过最小二乘拟合高斯分布(Gaussian profile),一种非线性函数:α*exp(-(x-μ)2/2σ2)
在这里,α表示一个标量,μ是期望值,而σ是标准差。示例代码:
#创建一个函数模型用来生成数据
def func(x, a, b, c):
return a*np.exp(-(x-b)**2/2*c**2))
#生成原始数据
x = np.linspace(0, 10, 100)
y = func(x, 1, 5, 2)
#对原始数据增加噪声
yn = y + 0.2*np.random.normal(size=len(x))
#使用curve_fit函数拟合噪声数据
popt, pcov = curve_fit(func, x, yn)
#popt返回最拟合给定的函数模型func的参数值
print(popt)
通过以上绘图,我们可以看出对高斯分布函数拟合的效果是可以接受的。
随着研究的深入,我们可以拟合一个多重高斯分布的一维数据集。现在将这个函数扩展为包含两个不同输入值的高斯分布函数。这是一个拟合线性光谱的经典实例,示例代码如下:
#二重高斯模型
def func(x, a0, b0, c0, a1, b1, c1):
return a0*np.exp(-(x - b0) ** 2/(2 * c0 ** 2)) + a1 * np.exp(-(x-b1) ** 2/(2 * c1 ** 2))
#生成原始数据
x = np.linspace(0, 20, 200)
y = func(x, 1, 3, 1, -2, 15, 0.5)
#对原始数据增加噪声
yn = y + 0.9 * np.random.normal(size=len(x))
#如果要拟合一个更加复杂的函数,提供一些估值假设对拟合效果更好
guesses = [1, 3, 1, 1, 15, 1]
#使用curve_fit函数拟合噪声数据
popt, pcov = curve_fit(func, x, yn, p0=guesses)
4.3.2 最小二乘拟合leastsq()函数
假设有一组实验数据(x[i], y[i]),我们知道它们之间的函数关系:y = f(x),通过这些已知信息,需要确定函数中的一些参数项。例如,如果f是一个线型函数f(x) = k*x+b,那么参数k和b就是我们需要确定的值。如果将这些参数用 p 表示的话,那么我们就是要找到一组 p 值使得如下公式中的S函数最小:
这种算法被称之为最小二乘拟合(Least-square fitting)。optimize模块提供了实现最小二乘拟合算法的函数leastsq(),leastsq是least square的简写,即最小二乘法。
下面是用leastsq()对线性函数进行拟合的程序,示例代码:
import numpy as np
from scipy import optimize # 从scipy库引入optimize模块
X = np.array([ 8.19, 2.72, 6.39, 8.71, 4.7, 2.66, 3.78 ])
Y = np.array([ 7.01, 2.78, 6.47, 6.71, 4.1, 4.23, 4.05 ])
def residuals(p):
#计算以p为参数的直线和原始数据之间的误差
k, b = p
return Y-(k*X+b)
# leastsq()使得residuals()的输出数组的平方和最小,参数的初始值为[1, 0]
r = optimize.leastsq(residuals, [1,0])
k, b = r[0]
print("k=", k, "b=", b)
输出拟合参数的结果:
k = 0.613495349193 b = 1.79409254326
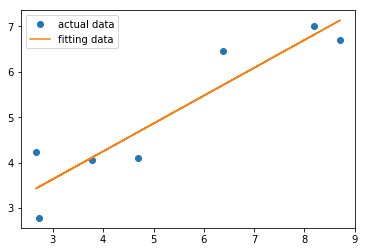
可以通过通过绘图对比真实数据和拟合数据的误差,示例代码;
import pylab as pl
pl.plot(X, Y, "o", label = "actual data")
pl.plot(X, k*X+b, label = "fitting data")
pl.legend(loc = "best")
pl.show()
绘图中的圆点表示真实数据点,实线表示拟合曲线,由此看出拟合参数得到的函数和真实数据大体一致。
接下来,用leastsq()对正弦波数据进行拟合,示例代码:
import numpy as np
from scipy.optimize import leastsq # 从scipy库的optimize模块引入leastsq函数
import pylab as pl # 引入绘图模块pylab,并重命名为pl
def func(x, p):
"""
数据拟合所用的函数: A*sin(2*pi*k*x + theta)
"""
A, k, theta = p
return A*np.sin(2*np.pi*k*x+theta)
def residuals(p, y, x):
"""
实验数据x, y和拟合函数之间的差,p为拟合需要找到的系数
"""
return y - func(x, p)
x = np.linspace(0, -2*np.pi, 100)
A, k, theta = 10, 0.34, np.pi/6 # 真实数据的函数参数
y0 = func(x, [A, k, theta]) # 真实数据
y1 = y0 + 2 * np.random.randn(len(x)) # 加入噪声之后的实验数据,噪声是服从标准正态分布的随机量
p0 = [7, 0.2, 0] # 第一次猜测的函数拟合参数
# 调用leastsq进行数据拟合
# residuals为计算误差的函数
# p0为拟合参数的初始值
# args为需要拟合的实验数据
plsq = leastsq(residuals, p0, args=(y1, x))
print ("actual parameter:", [A, k, theta]) # 真实参数
print ("fitting parameter", plsq[0]) # 实验数据拟合后的参数
pl.plot(x, y0, label="actual data") # 绘制真实数据
pl.plot(x, y1, label="experimental data with noise") # 带噪声的实验数据
pl.plot(x, func(x, plsq[0]), label="fitting data") # 拟合数据
pl.legend()
pl.show()
这个例子中我们要拟合的函数是一个正弦波函数,它有三个参数 A, k, theta ,分别对应振幅、频率、相角。假设我们的实验数据是一组包含噪声的数据 x, y1,其中y1是在真实数据y0的基础上加入噪声的到了。
通过leastsq函数对带噪声的实验数据x, y1进行数据拟合,可以找到x和真实数据y0之间的正弦关系的三个参数: A, k, theta。下面是程序的输出:
>>>actual parameter: [10, 0.34, 0.5235987755982988]
>>>fitting parameter [ 10.12646889 0.33767587 0.48944317]
我们看到拟合参数虽然和真实参数完全不同,但是由于正弦函数具有周期性,实际上拟合参数得到的函数和真实参数对应的函数是一致的。
4.3.3 标量函数极值求解fmin()函数
首先定义以下函数,然后绘制它,示例代码:
>>>import numpy as np
>>>from scipy import optimize
>>>import matplotlib.plot as plt
>>> def f(x):
... return x**2 + 10*np.sin(x)
>>> x = np.arange(-10, 10, 0.1)
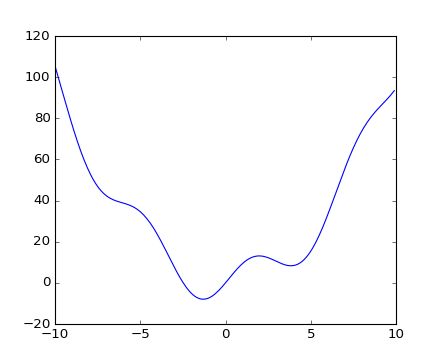
>>> plt.plot(x, f(x))
>>> plt.show()
如图所示,该函数大约在-1.3有个全局最小值,在3.8有个局部最小值。找到这个函数最小值一般而有效的方法是从初始点使用梯度下降法。BFGS算法是做这个的好方法,BFGS算法被认为是数值效果最好的拟牛顿法,是由Broyden,Fletcher,Goldfarb,Shanno四个人分别提出的,故称为BFGS校正。具体算法思想及解释请查阅相关资料,这里直接通过optimize.fmin_bfgs()函数求解最小值,示例代码:
>>> optimize.fmin_bfgs(f, 0)
Optimization terminated successfully.
Current function value: -7.945823
Iterations: 5
Function evaluations: 24
Gradient evaluations: 8
array([-1.30644003])
这个方法一个可能的问题在于,如果函数有局部最小值,算法会因初始点不同找到这些局部最小而不是全局最小,示例代码:
>>> optimize.fmin_bfgs(f, 3, disp=0)
array([ 3.83746663])
如果我们不知道全局最小值的邻近值来选定初始点,我们需要借助于耗费资源些的全局优化。为了找到全局最小点,最简单的算法是蛮力算法,该算法求出给定格点的每个函数值。示例代码:
>>>grid = (-10, 10, 0.1)
>>>xmin_global = optimize.brute(f, (grid, ))
>>>xmin_global
array([-1.30641113])
对于大点的格点,scipy.optimize.brute()变得非常慢。scipy.optimize.anneal()提供了使用模拟退火的替代函数。对已知的不同类别全局优化问题存在更有效率的算法,但这已经超出scipy的范围。为了找到局部最小,我们把变量限制在(0,10)之间,使用scipy.optimize.fminbound(),示例代码:
>>> xmin_local = optimize.fminbound(f, 0, 10)
>>> xmin_local
3.8374671...
下面的程序通过求解卷积的逆运算演示fmin的功能。
对于一个离散的线性时不变系统h, 如果它的输入是x,那么其输出y可以用x和h的卷积表示:
现在的问题是如果已知系统的输入x和输出y,如何计算系统的传递函数h;或者如果已知系统的传递函数h和系统的输出y,如何计算系统的输入x。这种运算被称为反卷积运算,是十分困难的,特别是在实际的运用中,测量系统的输出总是存在误差的。
下面用fmin计算反卷积,这种方法只能用在很小规模的数列之上,因此没有很大的实用价值,不过用来评价fmin函数的性能还是不错的。示例代码:
import scipy.optimize as opt
import numpy as np
def test_fmin_convolve(fminfunc, x, h, y, yn, x0):
"""
x (*) h = y, (*)表示卷积
yn为在y的基础上添加一些干扰噪声的结果
x0为求解x的初始值
"""
def convolve_func(h):
"""
计算 yn - x (*) h 的power
fmin将通过计算使得此power最小
"""
return np.sum((yn - np.convolve(x, h))**2)
# 调用fmin函数,以x0为初始值
h0 = fminfunc(convolve_func, x0)
print fminfunc.__name__
print "---------------------"
# 输出 x (*) h0 和 y 之间的相对误差
print "error of y:", np.sum((np.convolve(x, h0)-y)**2)/np.sum(y**2)
# 输出 h0 和 h 之间的相对误差
print "error of h:", np.sum((h0-h)**2)/np.sum(h**2)
print
def test_n(m, n, nscale):
"""
随机产生x, h, y, yn, x0等数列,调用各种fmin函数求解b
m为x的长度, n为h的长度, nscale为干扰的强度
"""
x = np.random.rand(m)
h = np.random.rand(n)
y = np.convolve(x, h)
yn = y + np.random.rand(len(y)) * nscale
x0 = np.random.rand(n)
test_fmin_convolve(opt.fmin, x, h, y, yn, x0)
test_fmin_convolve(opt.fmin_powell, x, h, y, yn, x0)
test_fmin_convolve(opt.fmin_cg, x, h, y, yn, x0)
test_fmin_convolve(opt.fmin_bfgs, x, h, y, yn, x0)
test_n(200, 20, 0.1)
运行结果:
fmin
---------------------
error of y: 0.000360456186137
error of h: 0.0122264525455
Optimization terminated successfully.
Current function value: 0.207509
Iterations: 96
Function evaluations: 17400
fmin_powell
---------------------
error of y: 0.000129249083036
error of h: 0.000300953639205
Optimization terminated successfully.
Current function value: 0.207291
Iterations: 20
Function evaluations: 880
Gradient evaluations: 40
fmin_cg
---------------------
error of y: 0.000129697740414
error of h: 0.000292820536053
Optimization terminated successfully.
Current function value: 0.207291
Iterations: 31
Function evaluations: 946
Gradient evaluations: 43
fmin_bfgs
---------------------
error of y: 0.000129697643272
error of h: 0.000292817401206
4.3.4 函数求解fsolve()
optimize库中的fsolve函数可以用来对非线性方程组进行求解,其基本调用形式是fsolve(func, x0)。
func(x)是计算方程组误差的函数,它的参数x是一个矢量,表示方程组的各个未知数的一组可能解,func返回将x代入方程组之后得到的误差;x0为未知数矢量的初始值。首先通过一个简单的示例,利用fsolve()函数求解当线性函数为0时,x的值,示例代码:
from scipy.optimize import fsolve
import numpy as np
line = lambda x:x+3
solution = fsolve(line, -2)
print(solution)
结果是[-3,]。通过以下绘图函数可以看出当函数等于0时,x轴的坐标值为-3,示例代码:
import pylab as pl
x = np.linspace(-5.0, 0, 100)
pl.plot(x,line(x), color="green",label = "function")
pl.plot(solution,line(solution), "o", label = "root")
pl.legend(loc = "best")
pl.show()
绘图结果:
下面我们通过一个简单的示例介绍一下两个方程交点的求解方法,示例代码:
from scipy.optimize import fsolve
import numpy as np
# 定义解函数
def findIntersection(func1, func2, x0):
return fsolve(lambda x: func1(x)-func2(x),x0)
# 定义两方程
funky = lambda x : np.cos(x / 5) * np.sin(x / 2)
line = lambda x : 0.01 * x - 0.5
# 定义两方程交点的取值范围
x = np.linspace(0, 45, 1000)
result = findIntersection(funky, line, [15, 20, 30, 35, 40, 45])
# 输出结果
print(result, line(result))
通过绘图函数可以看出交点值,示例代码:
import pylab as pl
pl.plot(x,funky(x), color="green",label = "funky func")
pl.plot(x,line(x), color="yellow",label = "line func")
pl.plot(result,line(result), "o", label = "intersection")
pl.legend(loc = "best")
pl.show()
绘图结果:
如果要对如下方程组进行求解的话:
- f1(u1,u2,u3) = 0
- f2(u1,u2,u3) = 0
- f3(u1,u2,u3) = 0
那么func可以如下定义:
def func(x):
u1,u2,u3 = x
return [f1(u1,u2,u3), f2(u1,u2,u3), f3(u1,u2,u3)]
下面是一个实际的例子,求解如下方程组的解:
- 5*x1 + 3 = 0
- 4*x0*x0 - 2*sin(x1*x2) = 0
- x1*x2 - 1.5 = 0
示例代码:
from scipy.optimize import fsolve
from math import sin,cos
def f(x):
x0 = float(x[0])
x1 = float(x[1])
x2 = float(x[2])
return [
5*x1+3,
4*x0*x0 - 2*sin(x1*x2),
x1*x2 - 1.5
]
result = fsolve(f, [1,1,1])
print (result)
输出结果为:
[-0.70622057 -0.6 -2.5 ]