Python深度学习（三）神经网络入门

本章涵盖了

• 神经网络的核心组件
• Keras概论
• 设置深度学习工作环境
• 使用神经网络来解决基本分类和回归问题

本章旨在让你开始使用神经网络来解决实际问题。您将巩固从第2章的第一个实际示例中获得的知识，并将所学知识应用于三个新问题，涉及到神经网络的三个最常见的用例:二分类、多分类和标量回归。
在这一章中，我们将更深入地了解我们在第二章中介绍的神经网络的核心组件:层、网络、目标函数和优化器。
我们将向您简要介绍Keras，这个Python深度学习库将贯穿全书。你将建立一个深度学习工作环境（通过TensorFlow，Keras，和GPU的支持）。我们将深入研究如何使用神经网络解决实际问题的三个介绍性示例:

• 分类影评为积极positive还是消极negative(二分类)
• 按主题分类新闻(多分类)
• 根据房地产数据估算房价(回归)

到本章结束时，您将能够使用神经网络来解决简单的机器问题，例如向量数据的分类和回归。然后，您将准备在第四章中开始构建一个更有原则的、理论驱动的机器学习理解。

3.1神经网络剖析

正如你在前几章看到的，训练神经网络围绕以下对象:

• 层，用于合并成网络(或模型)
• 输入数据和相应的目标
• 损失函数,定义了用于学习的反馈信号
• 优化器,这决定了学习如何进行

您可以将它们的交互可视化，如图3.1所示:网络由连接在一起的层组成，将输入数据映射到预期值。然后，损失函数将这些预期值与目标进行比较，产生一个损失值:一个衡量网络预测与预期匹配程度的指标。优化器使用这个损失值来更新网络的权重。

让我们仔细看看层、网络、损失函数和优化器。

3.1.1 layers: 深度学习的构建模块

神经网络的基础数据结构是layer，在第二章中已有介绍过。层是一个数据处理模块，它接受一个或多个张量作为输入，并输出一个或多个张量。有些层是无状态的，但更常见的是层有一个状态:层的权值，用随机梯度下降法学习的一个或几个张量，这些张量一起组成了网络的知识。
不同的层适用于不同的张量格式和不同类型的数据处理。例如，简单的矢量数据存储在二维张量的形状(samples,features)中，通常由紧密连接的层（densely connected）处理，也称为完全连接层或密集层(Keras中的密集类)。序列数据存储在形状为三维张量(samples,timesteps, features),中，通常由循环层（recurrent）处理，比如LSTM层。图像数据存储在4D张量中，通常由二维卷积层(Conv2D)处理。
你可以把layer看作深度学习的乐高积木，这个比喻是由Keras这样的框架明确表达出来的。在Keras中构建深度学习模型是通过剪切兼容的层来形成有用的数据转换管道来完成的。这里的层兼容性指的是每一层只接受特定形状的输入张量，并返回特定形状的输出张量。考虑下面的例子:

我们正在创建一个只接受作为输入2D张量的层，其中第一个维数是784(轴0，批处理维数是未指定的，因此任何值都会被接受)。这一层将返回一个张量，其中第一维变换为32。
因此，这个层只能连接到一个下游层，它需要32维向量作为它的输入。在使用Keras时，您不必担心兼容性，因为添加到模型中的层是动态构建的，以匹配进入层的形状。例如，假设您写下以下内容:

from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(32, input_shape=(784,)))
model.add(layers.Dense(32))

第二层没有接收输入形状参数——相反，它会自动推断出它的输入形状是之前层的输出形状。

3.1.2模型:层次网络

深度学习模型是一个有向的、无循环的层次图。最常见的实例是层的线性堆栈，将单个输入映射到单个输出。
但是随着你的深入，您将接触到更广泛的网络拓扑。一些常见的问题包括:

• 二分支网络
• 多线程网络
• 初始块（Inception blocks）

网络的拓扑定义了一个假设空间。你们可能记得第一章中，我们将机器学习定义为“利用反馈信号的引导，在预定义的可能性空间内，搜索一些输入数据的有用表示。”通过选择网络拓扑，你就限制了你的可能性空间(假设空间)到特定的一系列张量运算，将输入数据映射到输出数据。你接下来要找的是这些张量运算中涉及到的权重张量的一组很好的值。
选择合适的网络架构与其说是一门科学，不如说是一门艺术;尽管有一些你可以信赖的最佳实践和原则，但只有实践才能帮助你成为一个合适的神经网络架构师。接下来的几章将教给你构建神经网络的明确原则，帮助你培养对特定问题的直觉。

3.1.3 损失函数和优化器：配置学习过程的关键

一旦定义了网络架构，您仍然需要选择另外两件事:

• 损失函数(目标函数)-在训练中需要最小化的数值。它代表着对手头任务的成功程度的度量。
• 优化器——根据损失函数确定网络的更新方式。它实现了随机梯度下降(SGD)的一种特殊变体。

具有多个输出的神经网络可能具有多个损失函数(每个输出一个)。但梯度下降过程必须基于单个标量损失值;因此，对于多损失网络，所有损失(通过平均)合并成一个标量。
为正确的问题选择正确的目标函数是非常重要的:你的网络会走它能走的任何捷径，以最小化损失;因此，如果目标与手头任务的成功程度不完全相关，你的网络最终会做一些你可能不期望的结果。想象一个愚蠢的，万能的人工智能通过SGD进行训练，而目标函数选得很差:“最大化所有活着的人的平均幸福。”为了使它的工作更容易，这个人工智能可能会选择杀死除少数人之外的所有人，并专注于剩下的人的幸福——因为平均幸福不受剩下多少人的影响。那可能不是你想要的!只要记住，你建立的所有神经网络在降低损失功能上同样无情——所以明智地选择目标，否则你将不得不面对意想不到的副作用。
幸运的是，当涉及到诸如分类、回归和序列预测等常见问题时，您可以遵循一些简单的指导原则来选择正确的损失。例如，对于一个两类分类问题，您将使用二元交叉熵（binary crossentropy），对于一个多类分类问题使用分类交叉熵（categorical crossentropy），对于回归问题使用均方差（meansquared error），对于序列学习问题使用连接主义时间分类（connectionist temporal classification, CTC）等等。只有当你在研究真正新的研究问题时，你才需要开发出自己的目标函数。在接下来的几章中，我们将显式地详细说明在许多常见任务中应该选择哪些损失函数。

3.2 Keras简介

在本书中，代码示例使用Keras (https://keras.io)。Keras是Python的一个深度学习框架，它提供了一种方便的方式来定义和训练几乎任何类型的深度学习模型。Keras最初是为研究人员开发的，目的是实现快速实验。
Keras有以下关键特点:

• 它允许相同的代码在CPU或GPU上无缝运行。
• 它有一个友好的API,便于快速开发原型深度学习模型。
• 它内置支持卷积网络(convolutional networks，用于计算机视觉),复发性网络(recurrent networks，用于序列处理),以及两者的结合。
• 它支持任意网络体系结构:多输入和多输出模型,共享层,共享模型等等。这意味着Keras适用于构建任何深度学习模型，从生成式对抗性网络（generative adversarial network）到神经图灵机（neural Turing machine）。

Keras是以MIT license发布的，这意味着它可以在商业项目中自由使用。它兼容任何版本的Python，从 2.7到3.6(2017年中期)。
Keras拥有超过20万的用户，从初创公司和大公司的学术研究人员和工程师到研究生和业余爱好者。Keras在谷歌、Netflix、Uber、CERN、Yelp、Square以及数百家致力于解决各种问题的初创公司中都有应用。Keras也是机器学习竞赛网站Kaggle上一个很受欢迎的框架

3.2.1 Keras, TensorFlow, Theano, and CNTK

Keras是一个模型级库，提供了开发深度学习模型的高级构建模块。它不处理低级操作，如张量操作和微分。相反，它依赖于一个专门的、经过良好优化的张量库，充当Keras的后端引擎。不是选择单个张量库并将Keras的实现与该库绑定在一起，而是以模块化的方式处理问题(参见图3.3);因此，可以将几个不同的后端引擎无缝地插入到Keras中。目前，现有的三个后端实现是TensorFlow后端、Theano后端和Microsoft Cognitive工具包(CNTK)的后端。在未来，Keras可能会被扩展到使用更deep-learning的执行引擎。

TensorFlow、CNTK和Theano是当今深度学习的一些主要平台。Theano ( http://deeplearning.net/software/theano)由蒙特利尔大学的MILA实验室开发，TensorFlow ( www.tensorflow.org)由谷歌开发，CNTK( https://github.com/Microsoft/CNTK)由微软开发。您使用Keras编写的任何代码片段都可以与这些后端一起运行，而无需更改代码中的任何内容:在开发过程中，您可以无缝地在两者之间切换，这通常被证明是有用的——例如，如果这些后端中有一个对于特定任务来说速度更快的话。 我们建议将TensorFlow后端作为大多数深度学习需求的默认设置，因为它是最广泛采用的、可扩展的和有生产力的。
通过TensorFlow(或Theano，或CNTK)， Keras可以在cpu和gpu两者上无缝运行。在CPU上运行时，TensorFlow本身为张量操作包装了一个低级库，称为Eigen( http://feat.tuxfamily.org)。在GPU, TensorFlow封装了一个优化深度学习操作库,称之为NVIDIA CUDA深度神经网络库(cuDNN)。

3.2.2用Keras开发:快速概述

您已经看到了Keras模型的一个示例:MNIST示例。典型的Keras工作流看起来就像那个例子:

1. 定义你的训练数据:输入张量和目标张量。
2. 定义一个层(或模型)网络，用于将您的输入映射到您的目标。
3. 通过选择损失函数、优化器和一些要监控的指标来配置学习过程。
4. 通过调用模型的fit()方法迭代您的训练数据。

定义模型有两种方法:使用Sequential类(仅用于线性层堆栈，这是目前最常见的网络体系结构)或functionalAPI(用于层的有向无环图，它允许您构建完全任意的体系结构)。
作为复习，这里有一个使用Sequential类定义的两层模型(注意，我们将输入数据的预期形状传递给第一层):

from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(32, activation='relu', input_shape=(784,)))
model.add(layers.Dense(10, activation='softmax'))

下面是使用functional API定义的相同模型:

input_tensor = layers.Input(shape=(784,))
x = layers.Dense(32, activation='relu')(input_tensor)
output_tensor = layers.Dense(10, activation='softmax')(x)
model = models.Model(inputs=input_tensor, outputs=output_tensor)

通过functionalAPI，你可以操纵模型处理的数据张量，并将层应用到这个张量上，就好像它们是函数一样。

请注意，有关如何使用functional API的详细指南可以在第7章中找到。在第7章之前，我们只在代码示例中使用Sequential类。
一旦定义了模型体系结构，是否使用了Sequential模型或functional` API。以下所有步骤都是相同的。
学习过程是在编译步骤中配置的，在这个步骤中，您指定了模型应该使用的优化器和损失函数，以及您希望在训练期间监控的指标。这里有一个单损失函数的例子，这是目前最常见的情况:

from keras import optimizers
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss='mse',
metrics=['accuracy'])

最后，学习过程由通过fit()方法向模型传递输入数据(以及相应的目标数据)的Numpy数组组成，类似于在Scikit-Learn和其他几个机器学习库中所做的工作:

model.fit(input_tensor, target_tensor, batch_size=128, epochs=10)

在接下来的几章中，您将对哪种类型的网络架构适用于不同类型的问题，如何选择正确的学习配置，以及如何调整模型，直到它给出您想要的结果，建立一个坚实的直觉。我们将在3.4、3.5和3.6节中查看三个基本示例:一个二分类示例、一个多分类示例和一个回归示例。

3.3 设置深度学习工作环境

在您开始开发深度学习应用程序之前，您需要设置您的工作环境。强烈建议您在一个现代的NVIDIA GPU上运行深度学习代码，尽管这不是必须的。有些应用程序——特别是卷积网络的图像处理和循环神经网络（recurrent neural）的序列处理——在CPU上的速度会非常慢，甚至是一个快速的多核CPU。甚至对于实际可以在CPU上运行的应用程序，您通常会看到使用现代GPU的速度提高了5到10倍。如果您不想在您的机器上安装GPU，您可以考虑在AWS EC2 GPU实例或谷歌云平台上运行您的实验。但是请注意随着时间的推移，云GPU实例可能变得昂贵。
无论您是在本地运行还是在云中运行，最好使用Unix工作环境。虽然在Windows上使用Keras在技术上是可能的(所有三个Keras后端都支持Windows)，但我们不推荐它。在附录A的安装说明中，我们将考虑Ubuntu机器。如果你是Windows用户，让一切正常运行的最简单的解决方案就是在你的机器上设置一个Ubuntu双启动。这似乎是一个麻烦，但从长远来看，使用Ubuntu会节省很多时间和麻烦。
注意，为了使用Keras，您需要安装TensorFlow或CNTK或Theano (如果你想在这三个后端之间来回切换，也可以选择全部)。在这本书中，我们将重点介绍TensorFlow，并给出一些与Theano相关的简单说明。我们不覆盖CNTK的说明。

3.3.1 Jupyter记事本:进行深度学习实验的首选方式

Jupyter notebook是进行深度学习实验的好方法——尤其是本书中的许多代码示例。它们广泛应用于数据科学和机器学习领域。notebook是一个由Jupyter notebook应用程序(https://jupyter.org)生成的文件，您可以在浏览器中编辑它。它将Python代码的执行能力与丰富的文本编辑功能结合在一起，以注释您正在做的事情。notebook还允许你将长时间的实验分解成更小的部分，这些部分可以独立执行，这使得开发具有交互性，并且意味着如果在实验后期出现问题，你不必重新运行之前的所有代码。
我们建议使用Jupyter notebook开始使用Keras，尽管这不是一个要求:您还可以运行独立的Python脚本或从PyCharm等IDE中运行代码。本书中的所有代码示例都可以作为开源 notebooks使用;你可以从这本书的网站www.manning.com/books/deep-learning-with-python获取。

3.3.2 让Keras跑起来:两个选项

为了开始实践，我们建议以下两种选项之一:

• 使用官方的EC2深度学习AMI (https://aws.amazon.com/amazonai/amis)，在EC2上以Jupyter notebook方式运行Keras实验。如果您的本地机器上还没有GPU，请这样做。附录B提供了一步一步的指南。
• 在本地Unix工作站上从头开始安装所有内容。然后，您可以运行本地Jupyter notebook或常规Python代码库。如果你已经有一个高端的英伟达GPU，那就这么做。附录A提供了一个特定于ubuntu的分步指南。
  让我们更仔细地看一看选择一个选项而不是另一个选项所涉及的一些妥协。

3.3.3在云计算中运行深度学习工作:利弊

如果你还没有一个可以用于深度学习的GPU(一个最近发布的高端NVIDIA GPU)，以在云端进行深度学习实验，这是一种简单、低成本的方式，让您无需购买任何额外的硬件即可开始工作。如果您正在使用Jupyter notebook，那么在云端运行的体验与在本地运行没什么不同。从2017年年中开始，让深度学习变得最容易的云服务无疑是AWS EC2。附录B提供了在EC2 GPU实例上运行Jupyter notebooks的逐步指南。
但如果你是深度学习的忠实用户，这种设置在很长一段时间内都是不可持续的，甚至在几个星期内也是不可持续的。EC2实例非常昂贵:附录B中推荐的实例类型(p2.xlarge instance在2017年年中的价格为每小时0.90美元，它不会为你提供太多电力。同时，一个坚实的消费阶层，GPU的价格在1000美元到1500美元之间——随着时间的推移，这个价格是相当稳定的，即使这些GPU的规格不断改进。如果您对深度学习很认真，您应该使用一个或多个gpu建立一个本地工作站。
简而言之，EC2是一个很好的入门方法。您可以完全在EC2 GPU实例上遵循本书中的代码示例。但如果你想成为深度学习的超级用户，那就拥有自己的gpu。

3.3.4 深度学习最好的GPU是什么?

如果你要买GPU，你应该选择哪一个?首先要注意的是它一定是NVIDIA GPU。英伟达是迄今为止唯一一家在深度学习方面投入巨资的图形计算公司，而现代深度学习框架只能在英伟达卡上运行。
2017年年中，我们推荐NVIDIA TITAN Xp作为市场上最好的深度学习卡。对于较低的预算，您可能需要考虑使用GTX 1060。如果你是在2018年或更晚的时候阅读这些页面，花点时间在网上寻找更新鲜的推荐，因为每年都会有新的款式出现。
从本节开始，我们将假设您可以访问具有以下功能的机器(安装好Keras和它的依赖)——最好有GPU支持。确保在继续之前完成这个步骤。仔细阅读附录中的逐步指南，如果需要进一步的帮助，可以上网查找。关于如何安装Keras和常见的深度学习依赖关系的教程很多。
我们现在可以深入研究Keras的实际例子。

3.4 电影评论分类:一个二元分类的例子

二分类或二元分类可能是应用最广泛的机器学习问题。在本例中，您将学习如何根据评论的文本内容将电影评论分为正面评论和负面评论。

3.4.1 IMDB数据集

您将使用IMDB数据集:一套50,000份高度两极化评论的互联网电影数据库。它们分为25000条训练评论和25000条测试评论，每一组由50%的负面评论和50%的正面评论组成。
为什么要使用单独的训练和测试集?因为你永远不应该用你用来训练它的数据来测试一个机器学习模型!仅仅因为模型在其训练数据上表现良好并不意味着它将在它从未见过的数据上表现良好;您所关心的是您的模型在新数据上的性能(因为您已经知道了您的训练数据的标签——显然您不需要您的模型来预测这些数据)。例如 ，您的模型最终可能只是记住了训练样本与其目标之间的映射，这对于预测模型从未见过的数据的目标来说是无用的。我们将在下一章更详细地讨论这一点。
与MNIST数据集一样，IMDB数据集也附带在Keras中。它已经经过预处理:评论(单词序列)已经被转换成整数序列，其中每个整数代表字典中的一个特定单词。
下面的代码将加载数据集(当您第一次运行它时，大约80 MB的数据将下载到您的计算机)。

Listing 3.1 Loading the IMDB dataset

from keras.datasets import imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)

参数num_words=10000意味着您将只保留训练数据中最常见的10,000个单词。罕见的单词将被丢弃。这允许您处理可管理大小的向量数据。
train_data和test_data变量是review(评论)的列表;每个评论都是一个单词索引列表(编码一个单词序列)。train_label和test_label是0和1的列表，0代表否定，1代表肯定:

>>> train_data[0]
[1, 14, 22, 16, ... 178, 32]
>>> train_labels[0]
1

因为你把自己限制在最常用的1万个单词，所以没有一个单词的索引超过1万个:

>>> max([max(sequence) for sequence in train_data])
9999

下面是如何快速将这些评论翻译回英语的方法单词:

3.4.2 准备数据

你不能把整数列表输入神经网络。你必须把列表变成张量。有两种方法:

• 填补你的列表,这样他们都有相同的长度,把它们变成一个整数形状张量(samples,word_indices),然后在网络的第一层使用一个能够处理这种整数张量的层(嵌入(Embedding)层，我们将在本书后面详细介绍)。
• 将列表编码为0和1的向量(One-hot encode)。这将意味着，例如，将序列[3,5]转换成10000维的向量，除了指标3和5，所有的0都是0，也就是1。然后，可以使用密集(Dense)层作为网络的第一层，能够处理浮点向量数据。
  让我们使用后一种解决方案对数据进行矢量化，您将手动对数据进行矢量化，以获得最大的清晰度。

Listing 3.2 Encoding the integer sequences into a binary matrix

现在样例变成这样子:

>>> x_train[0]
array([ 0., 1., 1., ..., 0., 0., 0.])

你也应该对你的标签进行矢量化，这很简单:

y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')

现在数据已经准备好输入神经网络。

3.4.3 构建你的network

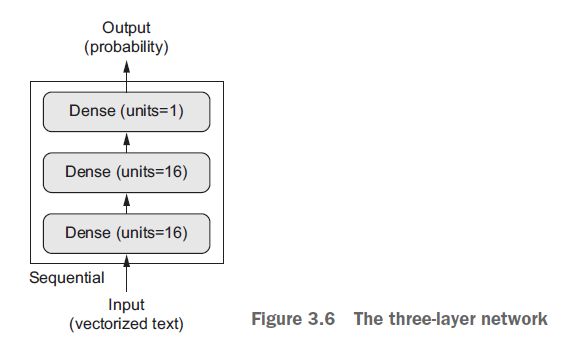
输入数据是向量，标签是标量(1和0):这是您遇到的最简单的设置。在这种问题上表现良好的一种网络是一个简单的堆栈，由完全连接(密集Dense)层与relu激活函数构成：Dense(16,activation='relu')。传递给每个Dense层的参数(16)是该层的隐藏单元（hidden unit）数。隐藏单元是层表示空间中的维度。
你可能还记得在第2章中，每个这样的密集层都有一个relu激活实现了以下张量操作链:

output = relu(dot(W, input) + b)

有16个隐藏单元意味着权重矩阵W将有形状(input_dimension，16):与W的点积将把输入数据投影到一个16维的表示空间上(然后加上偏差向量b，再应用relu运算)。您可以直观地理解表示空间的维数，即“在学习内部表示时，您允许网络拥有多大的自由度”。拥有更多的隐藏单元(高维表示空间)可以让网络学习更复杂的表示，但这会使网络的计算成本更高，并可能导致学习不需要的模式(模式将提高训练数据的性能，但不会提高测试数据的性能)
对于这样一堆密集层，有两个关键的架构决策需要做出:

• 使用多少个layers
• 针对每个layer，选取多少个hidden unit

在第四章，你将学习正式的原则来指导你做出这些选择。就目前而言，您必须相信我的架构选择:

• 两个中间层，每个层有16个隐藏单元
• 第三层将输出关于当前评论情绪的标量预测

中间层使用relu作为激活函数，最后一层使用sigmoid激活，输出一个概率(0到1之间的值，指示样本有多大可能具有目标“1”:评论有多大可能是正面的)。relu(整流线性单元)是一个函数，它的作用是消除负值(参见图3.4)，而sigmoid将任意值“压缩”到[0,1]区间(参见图3.5)，输出一些可以解释为概率的东西。

线性整流函数
Sigmoid函数

图3.6显示了网络的外观。这是Keras的实现，类似于之前看到的MNIST的例子。

Listing 3.3 The model definition

from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

• 什么是激活函数，为什么它们是必要的?
  如果没有像relu(也称为非线性)这样的激活函数，Dense层将由两个线性操作组成——点积和一个加法:
  output = dot(W, input) + b
  因此，该层只能学习输入数据的线性变换(仿射变换,affine transformations)):该层的假设空间是输入数据到16维空间的所有可能的线性变换的集合。这样的假设空间过于有限，不会从多层表示中获益，因为一大堆线性层仍然会实现线性操作:添加更多的层不会扩展假设空间。
  为了获得一个更丰富的假设空间，从深度表示中获益，你需要一个非线性，或者激活函数。relu是深度学习中最受欢迎的激活函数，但是还有很多其他的候选函数，它们都有同样奇怪的名字:prelu, elu等等。

最后，您需要选择损失函数和优化器。因为你面临一个二元分类问题网络的输出是一个概率(你用一个s型激活单元层结束你的网络)，最好选用binary_crossentropy loss函数。这不是唯一可行的选择:例如，您可以使用mean_squared_error。但是当你处理输出概率的模型时，交叉熵(Crossentropy)通常是最好的选择。交叉熵是信息领域中的一个量测量概率分布之间的距离的理论，在这种情况下，测量真实分布和预测之间的距离的理论。
下面是使用rmsprop优化器和binary_crossentropy loss函数配置模型的步骤。请注意，您还将在训练期间监控accuracy:

Listing 3.4 Compiling the model

model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['accuracy'])

您正在将优化器、损失函数和度量作为字符串传递，这是可能的，因为rmsprop、binary_crossentropy和accuracy都打包为Keras的一部分。有时，您可能希望配置优化器的参数，或者传递一个自定义损失函数或度量函数。前者可以通过将优化器类实例作为optimizer参数传递来实现，如清单3.5所示;后者可以通过将函数对象作为loss和/或metrics参数传递来完成，如清单3.6所示。

Listing 3.5 Configuring the optimizer

from keras import optimizers
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss='binary_crossentropy',
metrics=['accuracy'])

Listing 3.6 Using custom losses and metrics

from keras import losses
from keras import metrics
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss=losses.binary_crossentropy,
metrics=[metrics.binary_accuracy])

3.4.4 验证你的方法

为了在训练期间监控模型对以前从未见过的数据的准确性，您将通过从原始训练数据中分离10,000个样本来创建一个验证集。

Listing 3.7 Setting aside a validation set

x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]

现在，您将对模型以小批量512个样本，进行20次epoch (x_train和y_train张量中的所有样本进行20次迭代)。与此同时，你将监测你分开的10,000个样品的损失和准确性。您可以将验证数据作为validation_data参数传递。

Listing 3.8 Training your mode

model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val, y_val))

在CPU上，每次迭代将花费不到2秒的时间——训练在20秒内结束。在每一个迭代结束时，当模型计算它对10,000个验证数据样本的损失和准确性时，会有一个轻微的暂停。
注意，对model.fit()的调用返回一个History对象。这个对象有一个成员history，这是一个字典，包含了所有在训练期间发生的数据。让我们来看看:

>>> history_dict = history.history
>>> history_dict.keys()
[u'acc', u'loss', u'val_acc', u'val_loss']

该词典包含4个条目:在训练和验证期间监视的每个度量值有一个条目。在下面的两个list中，我们使用Matplotlib并排绘制训练和验证损失(参见图3.7)，以及训练和验证准确性(参见图3.8)。注意，由于网络的随机初始化不同，您自己的结果可能略有不同。

Listing 3.9 Plotting the training and validation loss

import matplotlib.pyplot as plt
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(acc) + 1)
plt.plot(epochs, loss_values, 'bo', label='Training loss')
plt.plot(epochs, val_loss_values, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

Listing 3.10 Plotting the training and validation accuracy

plt.clf()
acc_values = history_dict['acc']
val_acc_values = history_dict['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

如你所见，训练损失随时间的变化而减小，训练精度(accuracy)随时间的变化而增加。这就是您在运行梯度下降优化时所期望的——您试图最小化的数量应该随着每次迭代而减少。但验证损失和准确性却并非如此:它们似乎在第四次迭代达到顶峰。这是我们之前警告过的一个例子: 在训练数据上表现更好的模型不一定会在以前从未见过的数据上表现更好。确切地说，您看到的是过度拟合:在第二个阶段之后，您正在对训练数据进行过度优化，最终您将学习到特定于训练数据的表示，而不是泛化到训练集之外的数据。
在这种情况下，为了防止过度训练，你可以在3次迭代后停止训练。通常，您可以使用一系列技术来减轻过度拟合，我们将在第4章中介绍。
让我们从零开始训练一个新的网络，为期四个迭代，然后在测试数据上评估它。

Listing 3.11 Retraining a model from scratch

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(x_train, y_train, epochs=4, batch_size=512)
results = model.evaluate(x_test, y_test)

最终的结果如下：

>>> results
[0.2929924130630493, 0.88327999999999995]

这种相当简单的方法的准确率达到88%。使用最顶尖的方法，您应该能够接近95%。

3.4.5 使用训练过的网络对新数据进行预测

在训练了网络之后，您将希望在实际环境中使用它。你可以使用预测方法产生正面评论的可能性:

>>> model.predict(x_test)
array([[ 0.98006207]
[ 0.99758697]
[ 0.99975556]
...,
[ 0.82167041]
[ 0.02885115]
[ 0.65371346]], dtype=float32)

如您所见，对于某些样本(0.99或以上，或0.01或更少)，网络是自信的，而对于其他样本(0.6或0.4)，网络是不自信的。

3.4.6进一步实验

以下实验将帮助说服你，你的架构选择都相当合理,但仍有改进的余地:

• 你使用两个隐藏层。尝试使用一个或三个隐藏层，看看这样做如何影响验证和测试准确性。
• 尝试使用层有更多隐藏的单位或更少的隐藏单位:32单元,64单元等等。
• 尝试使用mse代替binary_crossentropy损失函数。
• 尝试使用tanh激活函数(一种在神经网络早期很流行的激活函数)而不是relu。

3.4.7结束

以下是你应该从这个例子中吸取的教训:

• 您通常需要对原始数据进行相当多的预处理，以便能够将其作为张量输入到神经网络中。单词序列可以编码为二进制向量，但也有其他编码选项。
• 使用relu激活函数的Dense层可以解决广泛的问题(包括情绪分类)，你可能会经常使用它们。
• 在二分类问题(两个输出类)中，网络应该以一个（隐藏）单元和一个sigmoid激活函数的密集（Dense）层结束:网络的输出应该是0到1之间的标量，编码一个概率。
• 在二元分类问题上有这样一个标量sigmoid输出的场景，您应该使用的损失函数是binary_crossentropy。
• 无论您有什么问题，rmsprop优化器通常都是一个足够好的选择。这是你不用担心的一件事。
• 随着他们在训练数据上的进步，神经网络最终开始过拟合，最终在他们从未见过的数据上得到越来越糟糕的结果。一定要始终监视训练集之外的数据的性能。

3.5 分类新闻专线:一个多分类的例子

在上一节中，您看到了如何使用紧密连接(densely connected)的神经网络将向量输入分类为两个相互排斥的类。但是如果你有两种以上的分类会发生什么呢?
在本节中，您将构建一个网络，将路透社新闻专线分为46个相互排斥的主题。因为你有很多类，这个问题是一个多分类的实例;而且，由于每个数据点都应该被划分为一个类别，因此问题更具体地说就是一个单标签、多分类（single-label, multiclass classification.）的实例。如果每个数据点可能属于多个类别(在本例中是主题)，那么您将面临一个多标签、多分类（multilabel, multiclass classification）问题。

3.5.1路透社数据集

您将使用路透社数据集(Reuters dataset)，这是一组简短的新闻专线及其主题，由路透社(Reuters)于1986年发布。这是一个简单的，广泛使用的用于文本分类的玩具数据集。有46个不同的主题;有些主题比其他主题更有代表性，但是每个主题在训练集中至少有10个例子。
像IMDB和MNIST一样，路透数据集也是Keras的一部分。让我们来看看。

Listing 3.12 Loading the Reuters dataset

from keras.datasets import reuters
(train_data, train_labels), (test_data, test_labels) = reuters.load_data(
num_words=10000)

与IMDB数据集一样，参数num_words=10000将数据限制为在数据中发现的10000个最常见的单词。
您有8,982个培训示例和2,246个测试示例：

>>> len(train_data)
8982
>>> len(test_data)
2246

与IMDB评论一样，每个示例都是一个整数列表(单词索引):

>>> train_data[10]
[1, 245, 273, 207, 156, 53, 74, 160, 26, 14, 46, 296, 26, 39, 74, 2979,
3554, 14, 46, 4689, 4329, 86, 61, 3499, 4795, 14, 61, 451, 4329, 17, 12]

下面是你如何把它解码成文字的方法，以满足你的好奇心。

Listing 3.13 Decoding newswires back to text

与示例关联的标签是0到45之间的整数——主题索引

>>> train_labels[10]
3

3.5.2 准备数据

您可以使用与前面示例完全相同的代码对数据进行矢量化

Listing 3.14 Encoding the data

要对标签进行矢量化，有两种可能:您可以将标签列表转换为整数张量，或者您可以使用one-hot编码。one-hot编码是一种广泛用于分类数据的格式，也称为分类编码（categorical encoding）。有关one-hot编码的更详细解释，请参阅第6.1节。在本例中，标签的one-hot编码包括将每个标签嵌入为一个全零向量，在标签索引的位置用1代替。这里有一个例子:

注意，在Keras中有一种内置的方法可以做到这一点，您已经在MNIST示例中看到了这一点:

from keras.utils.np_utils import to_categorical
one_hot_train_labels = to_categorical(train_labels)
one_hot_test_labels = to_categorical(test_labels)

3.5.3 构建网络

这个主题分类问题与前面的电影评论分类问题类似:在这两种情况下，您都试图对简短的文本片段进行分类。但是这里有一个新的限制:输出类的数量从2个增加到46个。输出空间的维数要大得多。
在您使用过的Dense层堆栈中，每个层只能访问前一层输出的信息。如果有一层掉了一些与分类问题相关的信息，这些信息后续的层永远无法恢复:每一层都可能成为信息瓶颈。在前面的示例中，您使用了16维的中间层，但是一个16维的空间可能太有限，无法学习如何分离46个不同的类:这样的小层可能成为信息瓶颈，永久地删除相关信息。
因此，您将使用更大的层，共64个单元。

Listing 3.15 Model definition

from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))

关于这个架构，还有两件事需要注意:

• 以大小为46的Dense层结束网络。这意味着对于每个输入样本，网络将输出一个46维的向量。这个向量中的每个元素
  (每个维度)将编码不同的输出类。
• 最后一层使用softmax激活。您在MNIST示例中看到了这种模式。这意味着网络将输出46个不同输出类的概率分布——对于每个输入样本，网络将产生一个46维的输出向量，其中output[i]是样本属于i类的概率。

在这种情况下，最好的损失函数是categorical_crossentropy。它测量了两个概率分布之间的距离:这里，网络输出的概率分布和标签的真实分布之间的距离。通过最小化这两个分布之间的距离，您可以训练网络输出尽可能接近真实标签的内容。

Listing 3.16 Compiling the mode

model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])

3.5.4 验证你的方法

让我们在训练数据中分别设置1000个样本作为验证集。

x_val = x_train[:1000]
partial_x_train = x_train[1000:]
y_val = one_hot_train_labels[:1000]
partial_y_train = one_hot_train_labels[1000:]s

现在，让我们对网络进行20次的训练

Listing 3.18 Training the model

history = model.fit(partial_x_train, partial_y_train,epochs=20,batch_size=512,validation_data=(x_val, y_val))

最后，让我们显示它的损失和精度曲线(见图3.9和3.10)。

Listing 3.19 Plotting the training and validation loss

import matplotlib.pyplot as plt
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

Listing 3.20 Plotting the training and validation accuracy

plt.clf()
acc = history.history['acc']
val_acc = history.history['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

网络在经历了九个迭代之后开始过拟合。让我们从零开始训练一个新的网络，历时9个迭代，然后在测试集中评估它。
Listing 3.21 Retraining a model from scratch

model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))
model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
model.fit(partial_x_train, partial_y_train, epochs=9, batch_size=512, validation_data=(x_val, y_val))
results = model.evaluate(x_test, one_hot_test_labels)

以下是最终结果:

>>> results
[0.9565213431445807, 0.79697239536954589]

这种方法的准确率达到约80%。对于平衡二分类问题，纯随机分类器的准确率为50%。但在这种情况下，它接近19%， 所以结果看起来相当不错，至少与随机基线相比是这样的:

>>> import copy
>>> test_labels_copy = copy.copy(test_labels)
>>> np.random.shuffle(test_labels_copy)
>>> hits_array = np.array(test_labels) == np.array(test_labels_copy)
>>> float(np.sum(hits_array)) / len(test_labels)
0.18655387355298308

3.5.5 对新数据进行预测

您可以验证模型实例的predict方法返回所有46个主题的概率分布。让我们为所有测试数据生成主题预测。

Listing 3.22 Generating predictions for new data

predictions = model.predict(x_test)

预测中的每一项都是长度为46的向量:

>>> predictions[0].shape
(46,)

这个向量系数的和是1:

>>> np.sum(predictions[0])
1.0

最大的条目是预测类——概率最高的类:

>>> np.argmax(predictions[0])
4

3.5.6 另一种处理标签和损失的方法

我们之前提到过，编码标签的另一种方法是将它们转换成整数张量，如下所示：

y_train = np.array(train_labels)
y_test = np.array(test_labels)

这种方法唯一会改变的是损失函数的选择。清单3.21中使用的loss函数categorical_crossentropy期望label遵循分类编码。对于整数标签，您应该使用sparse_categorical_crossentropy:

model.compile(optimizer='rmsprop',
loss='sparse_categorical_crossentropy',
metrics=['acc'])

这个新的损失函数在数学上仍然与categorical_crossentropy相同;它只是有一个不同的接口。

3.5.7具有足够大的中间层的重要性

我们在前面提到过，因为最终的输出是46维的，所以应该避免中间层的隐藏单元远远少于46个。现在让我们看看当你引入一个信息瓶颈时，如果中间层明显小于46维:例如，4维：

Listing 3.23 A model with an information bottleneck

model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(4, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(partial_x_train, partial_y_train, epochs=20, batch_size=128, validation_data=(x_val, y_val))

现在网络的validation accuracy达到了71%，下降了8%。这种下降主要是由于您试图将大量信息(需要足够的信息以恢复46个类的分离超平面)压缩到过低维的中间空间。网络能够将大部分必要的信息塞进这些八维表示中，但并不是全部。

3.5.8进一步的实验

• 尝试使用更大或更小的层:32个单元，128个单元等等。
• 你使用两个隐藏层。现在尝试使用一个隐藏层，或者三个隐藏层。

3.5.9 结尾

以下是你应该从这个例子中吸取的教训:

• 如果您试图在N个类中分类数据点，那么您的网络应该以大小为N的Dense层结尾。
• 在单标签、多类分类问题中，网络应该以softmax激活函数结束，这样它就会输出一个在N输出类上的概率分布。
• Categorical crossentropy几乎总是这种问题的损失函数。它使网络输出的概率分布与目标的真实分布之间的距离最小化。
• 在多类分类中有两种处理标签的方法:
  --通过分类编码(也称为one-hot编码)，并使用categorical_crossentropy作为损失函数对标签进行编码
  -- 将标签编码为整数，并使用sparse_categorical_crossentropy loss函数

• 如果需要将数据分类为大量的类别，则应该避免由于中间层太小而在网络中造成信息瓶颈

3.6预测房价:一个回归例子

前面的两个例子被认为是分类问题，目标是预测输入数据点的单个离散标签。另一种常见的机器学习问题是回归，它由预测连续值而不是离散标签组成:例如，给定的气象数据,预测明天的温度;或者给定它的规格,预测一个软件项目完成的时间.
注意: 不要混淆回归和logistic regression算法。令人困惑的是，logistic regression不是一种回归算法——而是一种分类算法。

3.6.1波士顿房价数据集

你将尝试利用给出的当时该郊区的数据点，比如犯罪率，当地房产税率等等，预测20世纪70年代中期波士顿某郊区的房价中值。您将使用的数据集与前面两个示例有一个有趣的区别。它的数据点相对较少:只有506个，分为404个训练样本和102个测试样本。以及输入数据中的每个特征(例如，犯罪率)有不同的规模。例如，有些值是概率，它们的值在0和1之间;另一些取1到1之间的值等等。

Listing 3.24 Loading the Boston housing dataset

from keras.datasets import boston_housing
(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()

查看下数据：

>>> train_data.shape
(404, 13)
>>> test_data.shape
(102, 13)

如您所见，您有404个训练样本和102个测试样本，每个样本都有13个数值特征，例如人均犯罪率、人均住房数量、高速公路的可达性等等。
目标是业主自住房屋的中值，单位为数千美元:

>>> train_targets
[ 15.2, 42.3, 50. ... 19.4, 19.4, 29.1]

价格一般在1万到5万美元之间。如果这听起来很便宜，请记住，这是在上世纪70年代中期，而且这些价格没有根据通胀进行调整。

3.6.2准备数据

如果将所有的神经网络值都包含在大不相同的范围内，那将是一个问题。网络可能能够自动适应这种异构数据，但它肯定会使学习变得更加困难。广泛的最佳实践来处理这样的数据是feature的normalization:对于输入数据中的每个特征(输入数据矩阵中的一列)，减去特征的平均值并除以标准差，使特征的中心为0，并且有一个单位标准差。这在Numpy中很容易做到。

Listing 3.25 Normalizing the data

mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
test_data -= mean
test_data /= std

注意，用于标准化测试数据的数值是使用训练数据计算的。您永远不应该在您的工作流中使用对测试数据进行任何数量的计算，即使对于像数据规范化这样简单的事情也是如此。

---

备注：0均值标准化(Z-score standardization)
0均值归一化方法将原始数据集归一化为均值为0、方差1的数据集，归一化公式如下：

其中，μ、σ分别为原始数据集的均值和标准。该种归一化方式要求原始数据的分布可以近似为高斯分布，否则归一化的效果会变得很糟糕。
在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，第二种方法(Z-score standardization)表现更好。

3.6.3 构建网络

由于可供使用的样本非常少，所以您将使用一个非常小的网络，其中包含两个隐藏层，每个层有64个单元。一般来说，您拥有的训练数据越少，过度拟合就越糟糕，使用一个小网络是缓解过度拟合的一种方法。

Listing 3.26 Model definition

网络以1个单元结束,没有激活函数(它将是一个线性层)。这是标量回归的一个典型设置(在你试图预测单个连续值的情况下)。应用激活函数将限制输出的范围,例如,如果将sigmoid激活函数应用到最后一层,则网络只能学会预测0到1之间的值。在这里，因为最后一层是纯线性的，网络可以自由地学习在任何范围内预测值。
注意，您使用mse损失函数---均方差(即预测和目标差的平方)来编译网络。这是一个广泛用于回归问题的损失函数。
您还在训练期间监视一个新的度量:平均绝对误差(MAE，备注：MAD=(x-mean(x))./n;)。它是预测和目标之间差值的绝对值。例如，在这个问题上的平均误差为0.5美元意味着你的预测平均误差为500美元。

3.6.4使用K-fold验证来验证您的方法（备注:交叉验证法）

为了评估您的网络，同时不断调整它的参数(例如用于训练的epochs的数量)，您可以将数据分为训练集和验证集，就像前面的示例所做的那样。但是由于数据点太少，验证集最终会非常小(例如，大约100个示例)。因此，验证分值可能会根据您选择使用哪些数据点进行验证，以及您选择了哪些数据点进行训练而发生很大的变化:根据验证分割，验证分值可能有很大的差异。这将妨碍您可靠地评估您的模型。
这种情况下的最佳实践是使用K-fold交叉验证(参见图3.11)。它包括将可用数据分成K个分区(通常K = 4或5)，实例化K个相同的模型，并在K - 1分区上对每个模型进行训练，同时对其余分区进行评估。使用的模型的验证分数是得到的K个验证分数的平均值。就代码而言，这很简单。

Listing 3.27 K-fold validation

在num_epochs = 100中运行这个程序会得到以下结果:

>>> all_scores
[2.588258957792037, 3.1289568449719116, 3.1856116051248984, 3.0763342615401386]
>>> np.mean(all_scores)
2.9947904173572462

不同的运行确实显示了相当不同的验证分数，从2.6到3.2。平均值(3.0)比任何一个分数都要可靠得多——这就是K-fold交叉验证的全部要点。在这种情况下，你平均损失了3000美元，考虑到价格从1万美元到5万美元，这是很重要的。
让我们试着把网络训练得更长一点:500次迭代。为了记录模型在每个epoch中的表现，您将修改训练循环以保存每次epoch验证得分日志。

Listing 3.28 Saving the validation logs at each fold

然后，您可以计算所有折叠项的每个epoch MAE得分的平均值。

Listing 3.29 Building the history of successive mean K-fold validation scores

average_mae_history = [np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]

让我们绘制它;见图3.12

Listing 3.30 Plotting validation scores

import matplotlib.pyplot as plt
plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

由于规模问题和相对较高的方差，可能很难看到图。让我们做以下事情:

• 省略前10个数据点，这些数据点与曲线的其他部分的尺度不同。
• 将每个点替换为前面点的指数移动平均值，以获得平滑曲线。
  结果如图3.13所示

Listing 3.31 Plotting validation scores, excluding the first 10 data points

def smooth_curve(points, factor=0.9):
smoothed_points = []
for point in points:
    if smoothed_points:
       previous = smoothed_points[-1]
       smoothed_points.append(previous * factor + point * (1 - factor))
    else:
       smoothed_points.append(point)
return smoothed_points
smooth_mae_history = smooth_curve(average_mae_history[10:])
plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

根据这个图，验证MAE在80年代后停止明显的改善。过了这个点，你就开始过拟合了。
一旦你完成了优化模型的其他参数(除了epochs的数量外,您还可以调整隐藏层的大小),你可以用最好的参数，训练最终生产模型的训练数据,然后看看它的性能测试数据。

Listing 3.32 Training the final model

最终的结果是：

>>> test_mae_score
2.5532484335057877

你还差2550美元。

3.6.5 结尾

以下是你应该从这个例子中吸取的教训:

• 回归是使用不同于我们用于分类的损失函数来完成的。均方误差(Mean squared error, MSE)是一种常用的回归损失函数。
• 同样，用于回归的评价指标与用于分类的评价指标不同;当然，accuracy的概念并不适用于回归。一个常见的回归指标是平均绝对误差(MAE)。
• 当输入数据中的特征具有不同范围的值时，每个特征都应该作为预处理步骤独立地进行缩放。
• 当可用数据很少时，使用K-fold验证是可靠地评估模型的好方法。
• 当可用的训练数据很少时，最好使用一个隐藏层很少的小网络(通常只有一个或两个)，以避免严重的过拟合。

章节总结

• 现在您可以处理向量数据上最常见的机器学习任务:二分类、多分类和标量回归。本章前面的“总结”部分总结了关于这类任务的要点。
• 在将原始数据输入神经网络之前，通常需要对其进行预处理。
• 当您的数据具有不同范围的特性时，作为预处理的一部分，独立地缩放每个特性。
• 随着训练的进行，神经网络最终开始过适应，并在从未见过的数据上得到更糟糕的结果。
• 如果你没有太多的训练数据，使用一个只有一两个隐藏层的小网络，以避免严重的过度拟合。
• 如果您的数据被划分为许多类别，如果您使中间层太小，可能会导致信息瓶颈。
• 对比分类，回归使用不同的损失函数和不同的评价指标。
• 当您处理少量数据时，K-fold验证可以帮助可靠地评估您的模型。

---

备注：关于指数平均数指标：https://baike.baidu.com/item/EMA，要比较均价的趋势快慢时，用EMA更稳定；有时，在均价值不重要时，也用EMA来平滑和美观曲线。