傻叉树算是先告一段落了,但是二叉树(Binary Tree)有很多种特殊情况,如平衡二叉树(Balanced Binary Tree)、二叉查找树(Binary Search Tree)、完全二叉树(Complete Binary Tree)、满二叉树(Full Binary Tree)等等,并且满二叉树的国内外定义还不同......所以又出现了个完美二叉树(Perfect Binary Tree,完美二叉树和我们国内的满二叉树定义相同),哎,任重而道远呐!
- 目录:
算法:附录
算法(1):递归
算法(2):链表
算法(3):数组
算法(4):字符串
算法(5):二叉树
算法(6):二叉查找树
算法(7):队列和堆栈(附赠BFS和DFS)
算法(8):动态规划
算法(9):哈希表
算法(10):排序
算法(11):回溯法
算法(12):位操作
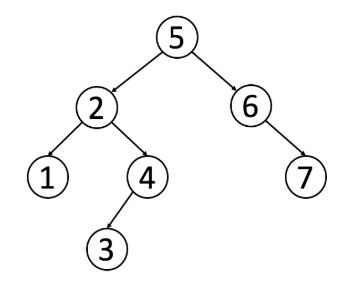
老规矩,先撒泼打滚卖萌求关注,先介绍一下啥是二叉查找树。简单来说,对于查找树的每一个节点,该节点的值大于等于其左子树当中任何一个节点值,同样的,该节点的值也小于等于其右子树当中任何一个节点的值。
如下图,便是一棵漂亮的BST:
了解了概念,大家可以先试试我们上一堂算法课当中学到的前中后序以及层级遍历,对上面那棵BST遍历试试。你会惊讶的发现(额,也可能没那么惊讶),当你使用中序遍历时,结果刚好是升序排列。所以,中序遍历,应当是BST最常用的遍历方法了把~
二叉查找树需要再提一提它的查找、增加、删除节点的操作。这些操作的时间复杂度都是 O(log(n)) (准确点说是 O(h),其中h代表树的深度),空间复杂度 O(1),强的要死!
查找:从根节点走起,根节点比目标值大,那去左子树,小,则上右子树。等于的话,那就你了,跟我走~
增加:很多策略,如果想要最小移动树节点的话,那就直接在叶子节点增加即可,跟查找同样步骤,一直到根节点,然后添加新节点即可。但是会导致这棵树长得较丑(不均衡)......
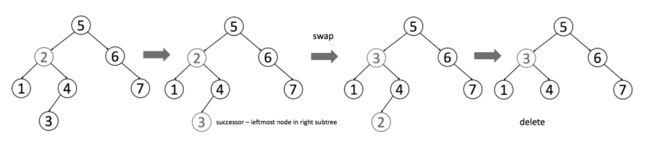
删除:删除节点略显复杂,当该节点没有子节点时,直接删;如果有一个子节点,那么用那个子树代替该位置;如果有两个子节点,则用其有序后继节点(右子树当中最左边的值)或前任节点(左子树当中最右边的值)替换该节点并删除该节点。最后一种情况比较复杂,我给大家偷了个图供大家参考。
基础概念就这么简单,知识的话,还是做题来的更夯实~
问题1:判断一棵树是否为BST。
大家可能心想,我只需要中序遍历,然后看是否为升序排列即可~ 当然,是个好方法,但是下面代码是按照BST的定义来编写的,可以更方便大家认识BST的基本概念~
该算法自顶向下,并记录了前面所有父节点属于的某个范围。如果下一个节点是左节点,则更新最大值(下一个节点应该小于该最大值和该节点的值);下一个节点是右节点,更新最小值(下一个节点应该大于该最小值和该节点的值)。有点绕,大家不要急,对,说你呢,别砸电脑了......慢慢理解。
输入:一棵可爱的二叉树,如下所示:
3
/ \
1 5
\ /
2 4
输出:True
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def isValidBST(root, large=float('inf'), small=float('-inf')):
if not root:
return True
if root.val <= small or root.val >= large:
return False
return isValidBST(root.left, min(large, root.val), small) and \
isValidBST(root.right, large, max(root.val, small))
if __name__ == '__main__':
node = head = TreeNode(3)
node.left = TreeNode(1)
node.right = TreeNode(5)
node.left.right = TreeNode(2)
node.right.left = TreeNode(4)
ans = isValidBST(head)
print(ans)
问题2:写一个BST迭代器。实现两个功能,hasNext()判断是否已经迭代到尾部,next()返回接下来的一个值。返回顺序按照升序排列。
输入:同上题
输出:1 2 3 4 5
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class BSTIterator:
def __init__(self, root: TreeNode):
self.stack = []
while root:
self.stack.append(root)
root = root.left
# @return a boolean, whether we have a next smallest number
def hasNext(self):
return len(self.stack) > 0
# @return an integer, the next smallest number
def next(self):
node = self.stack.pop()
x = node.right
while x:
self.stack.append(x)
x = x.left
return node.val
if __name__ == '__main__':
node = head = TreeNode(3)
node.left = TreeNode(1)
node.right = TreeNode(5)
node.left.right = TreeNode(2)
node.right.left = TreeNode(4)
obj = BSTIterator(head)
while obj.hasNext():
print(obj.next(),end=' ')
问题3:删除节点
输入:同问题1
输出:
4
/ \
1 5
\
2
本代码使用的方法就是上面所述的第一种删除方法~
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def deleteNode(root: TreeNode, key: int) -> TreeNode:
if not root: # if root doesn't exist, just return it
return root
if root.val > key: # if key value is less than root value, find the node in the left subtree
root.left = deleteNode(root.left, key)
elif root.val < key: # if key value is greater than root value, find the node in right subtree
root.right = deleteNode(root.right, key)
else: # if we found the node (root.value == key), start to delete it
if not root.right: # if it doesn't have right children, we delete the node then new root would be root.left
return root.left
if not root.left: # if it has no left children, we delete the node then new root would be root.right
return root.right
# if the node have both left and right children, we replace its value with the minmimum value in the right subtree and then delete that minimum node in the right subtree
temp = root.right
mini = temp.val
while temp.left:
temp = temp.left
mini = temp.val
root.val = mini # replace value
root.right = deleteNode(root.right, root.val) # delete the minimum node in right subtree
return root
if __name__ == '__main__':
node = head = TreeNode(3)
node.left = TreeNode(1)
node.right = TreeNode(5)
node.left.right = TreeNode(2)
node.right.left = TreeNode(4)
ans = deleteNode(head,3)
print(ans)
问题4:求最小公共祖先(Lowest Common Ancestor of a Binary Search Tree)
何为最小公共祖先?如下图,节点2和节点4的最小公共祖先为2(这里允许自己为自己的祖先,感觉这种逻辑,只有无性繁殖才能做到了把,,,),节点4和7的最小祖先为6,节点0和3的最小公共祖先为2......
二叉搜索树的找最小祖先比二叉树简单很多,我们可以充分利用其性质。除了最小公共祖先,其他的祖先有什么规律呢?我们发现,其他的祖先,会同时大于/(小于)这两个节点!而最小公共祖先,恰好是分岔口,要么大于其中一个,小于另一个,要么等于其中一个。知否?
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def lowestCommonAncestor(root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
while root:
if root.val > p.val and root.val > q.val:
root = root.left
elif root.val < p.val and root.val < q.val:
root = root.right
else:
return root
if __name__ == '__main__':
node = head = TreeNode(3)
node.left = TreeNode(1)
node.right = TreeNode(5)
node.left.right = TreeNode(2)
node.right.left = TreeNode(4)
ans = lowestCommonAncestor(head,node.left,node.left.right)
print(ans.val)
问题5:
# 四个问题不吉利,小编拍胸脯保证,马上(百年之内)把第五个问题补起来!