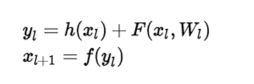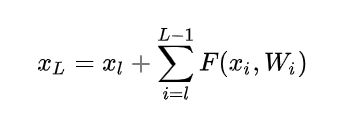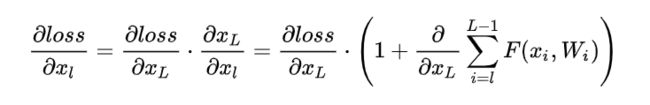【基础网络】ResNet论文详解（Deep Residual Learning for Image Recognition）

论文原文：https://arxiv.org/pdf/1512.03385.pdf

一、背景简介

深度学习中的基础网络的发展从ALexNet（5个卷积层）、VGG（19个卷积层）到GoogLeNet（22个卷积层），网络的结构在不断变深。这是因为更深的网络可以进行更加复杂的特征模式的提取，从而理论上更深的网络可以得到更好的结果。但是通过简单的叠加层的方式来增加网络深度，可能引来梯度消失/梯度爆炸的问题：

1. “梯度消失”：指的是即当梯度（小于1.0）在被反向传播到前面的层时，重复的相乘可能会使梯度变得无限小。
2. “梯度爆炸”：指的是即当梯度（大于1.0）在被反向传播到前面的层时，重复的相乘可能会使梯度变得非常大甚至无限大导致溢出。

因此随着网络深度的不断增加，常常会出现以下两个问题：

1. 长时间训练但是网络收敛变得非常困难甚至不收敛（这个问题很大程度已被标准初始化和中间标准化层解决）。
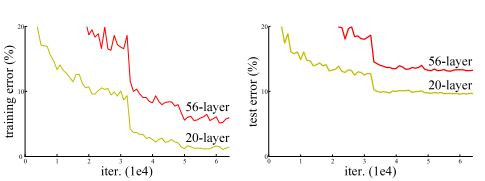
2. 网络性能会逐渐趋于饱和，甚至还会开始下降，可以观察到下图中56层的误差比20层的更多，故这种现象并不是由于过拟合造成的。这种现象称为深度网络的退化问题。

网络的训练性能包和

作者提出ResNet深度残差网络，成功解决了此类问题，使得即使在网络层数很深(甚至在1000多层)的情况下，网络依然可以得到很好的性能与效率。

二、残差学习

ResNet引入残差网络结构（residual network），即在输入与输出之间（称为堆积层）引入一个前向反馈的shortcut connection，这有点类似与电路中的“短路”，也是文中提到identity mapping（恒等映射y=x）。原来的网络是学习输入到输出的映射H(x)，而残差网络学习的是F(x)=H(x)−x。残差学习的结构如下图所示：

image

作者在文中提到：深层网络的训练误差一般比浅层网络更高；但是对一个浅层网络，添加多层恒等映射（y=x）变成一个深层网络，这样的深层网络却可以得到与浅层网络相等的训练误差。由此可以说明恒等映射的层比较好训练。

我们来假设：对于残差网络，当残差为0时，此时堆积层仅仅做了恒等映射，根据上面的结论，理论上网络性能至少不会下降。这也是作者的灵感来源，最终实验结果也证明，残差网络的效果确实非常明显。

但是为什么残差学习相对更容易？从直观上看残差学习需要学习的内容少，因为残差一般会比较小，学习难度小。另外我们可以从数学的角度来分析这个问题，首先残差单元可以表示为：

4.png

其中 x_{l} 和 x_{l+1} 分别表示的是第 l 个残差单元的输入和输出，注意每个残差单元一般包含多层结构。 F 是残差函数，表示学习到的残差，而h表示恒等映射， f 是ReLU激活函数。基于上式，我们求得从浅层 l 到深层 L 的学习特征为：

5.png

利用链式规则，可以求得反向过程的梯度：

6.png

式子的第一个因子表示的损失函数到达 L 的梯度，小括号中的1表明短路机制可以无损地传播梯度，而另外一项残差梯度则需要经过带有weights的层，梯度不是直接传递过来的。残差梯度不会那么巧全为-1，而且就算其比较小，有1的存在也不会导致梯度消失。所以残差学习会更容易。

三、残差学习的本质

残差网络的等价结构

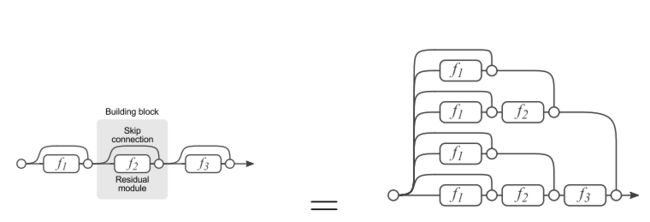
残差网络单元其中可以分解成右图的形式，从图中可以看出，残差网络其实是由多种路径组合的一个网络，直白了说，残差网络其实是很多并行子网络的组合，整个残差网络其实相当于一个多人投票系统（Ensembling）。

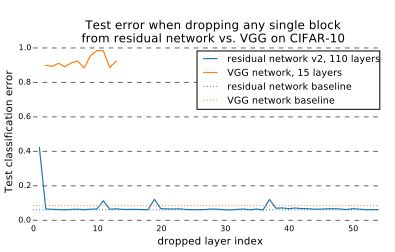
如果把残差网络理解成一个Ensambling系统，那么删除网络的一部分就相当于少一些投票的人，如果只是删除一个基本的残差单元，对最后的分类结果应该影响很小；而最后的分类错误率应该适合删除的残差单元的个数成正比的，另外一篇论文里的结论也印证了这个猜测。

下图是比较VGG和ResNet分别删除一层网络的分类错误率变化：

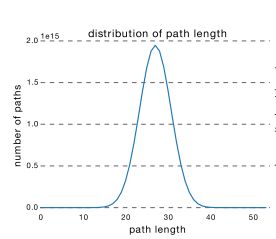
ResNet的确可以做到很深，但是从上面的介绍可以看出，网络很深的路径其实很少，大部分的网络路径其实都集中在中间的路径长度上，如下图所示：

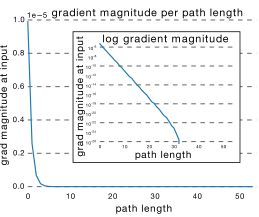
从这可以看出其实ResNet是由大多数中度网络和一小部分浅度网络和深度网络组成的，说明虽然表面上ResNet网络很深，但是其实起实际作用的网络层数并没有很深，我们能来进一步阐述这个问题，我们知道网络越深，梯度就越小，如下图所示：

而通过各个路径长度上包含的网络数乘以每个路径的梯度值，我们可以得到ResNet真正起作用的网络是什么样的，如下图所示：

我们可以看出大多数的梯度其实都集中在中间的路径上，论文里称为effective path。从这可以看出其实ResNet只是表面上看起来很深，事实上网络却很浅。

四、ResNet对比实验结果

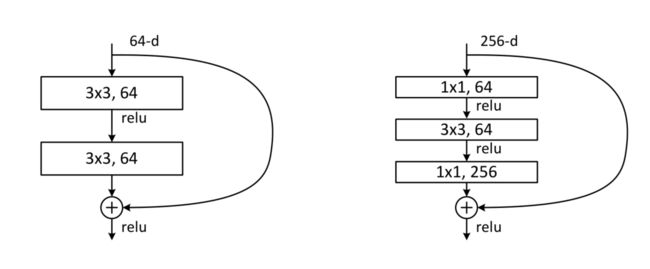
在创建更深的网络的时候，为了减轻训练时间的负担，ResNet并没有采取开始提出的隔两层添加一个shortcut connection。而是间隔1 * 1、3 * 3、1 * 1的三层网络，第一层用于降低维度，第三层用于升高维度。这种称为Bottleneck Architectures（瓶颈结构），结构见下图右侧：

image

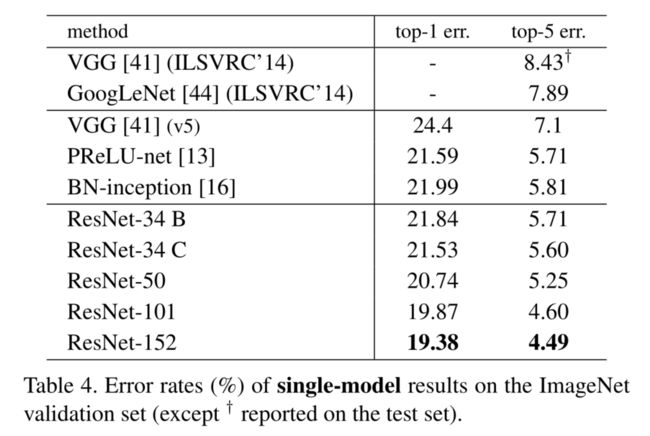
在ImageNet2012分类数据集上与之前最好的单模型对top-1、top-5结果进行了比较。34层基础残差网络取得了非常有竞争力的准确度。152层残差网络单模型对前5的验证错误率4.49%。这个单模型的结果优于所有以前的结果，见下表：

image

五、ResNet的其他细节

1、当堆积层的输入x和输出y不同维度的时候，即f是一个从低维向高维的映射时，这个时候不能简单的添加恒等映射作为shortcut connection，需要加上一个线性投影Ws，等于一个连接矩阵，这种结构称为投影结构

image

2、残差网络不仅可以运用到全连接层，还可以用到卷积层。

3、作者做了对比投影结构与恒等结构对实验结果的实验。发现投影结构对效果有细微提升，但是应该归功于投影连接增加的额外参数。

4、作者测试了1000层的残差网络，测试结果比110层更差，但是训练误差却与110层相似，造成这种现象应该是过拟合，对于小型的数据集，1000多层的网络属于杀鸡牛刀了，如果真的需要用到这么深的网络，可能需要更强的正则化。

5、ResNet在目标分类上有了非常好的泛化性能，作者将它应用到目标检测领域，将Faster R-CNN的基础网络用VGG-16与ResNet-101对比，性能均有大幅提升。