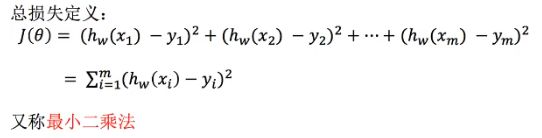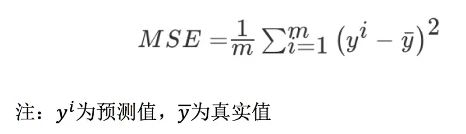09 线性回归及矩阵运算

09 线性回归及矩阵运算

线性回归

1. 定义：通过一个或者多个自变量与因变量之间进行建模的回归分析。其中可以为一个或者多个自变量之间的线性组合。

2. 一元线性回归：涉及到的变量只有一个
   多元线性回归：变量两个或以上

3. 通用公式：h(w) = w0 + w1x1 + w2x2 + ....= wTx
   其中w,x 为矩阵：wT=(w0, w1, w2) x=（1，x1, x2)T

回归的应用场景 （连续型数据）

1. 房价预测
2. 销售额预测 （广告，研发成本，规模等因素）
3. 贷款额度

线性关系模型

1. 定义： 通过属性 (特征) 的线性组合来进行预测的函数：
   • f(x) = w1x1 + w2x2 + w3x3 + ...... + wdxd + b
   • w : weight (权重） b: bias (偏置项）
   • 多个特征： (w1:房子的面积， w2:房子的位置 ..)

损失函数（误差）

1. 《统计学习方法》 - 算法 ，策略， 优化

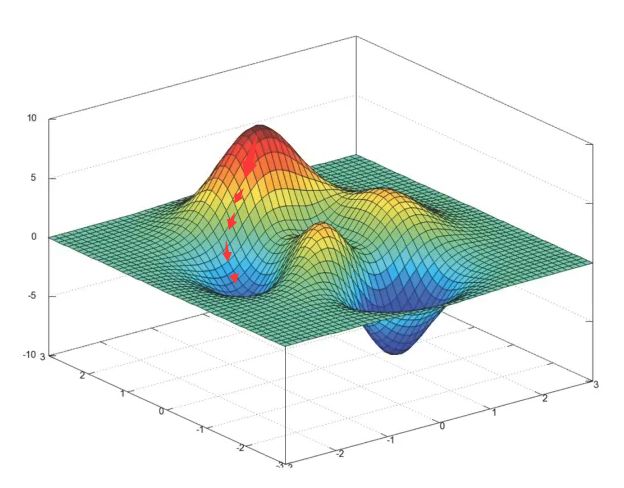
• 线性回归， 最小二乘法，正规方程 & 梯度下降

1. 损失函数（误差大小）

• yi 为第i个训练样本的真实值
• hw(xi)为第i个训练样本特征值组合预测函数 （预测值）
  

1. 寻找最优化的w
   1. 最小二乘法之正规方程 （直接求解到最小值，特征复杂时可能没办法求解）
      • 求解：w= (xTx）-1 xTy
      • X 为特征值矩阵，y为目标值矩阵
        
      • 缺点: 特征过于复杂时，求解速度慢
        

   2. 最小二乘法之梯度下降
      

      • 使用场景：面对训练数据规模庞大的任务
      • 超参数：a
        

线性回归算法案例

API

1. sklearn.linear_model.LinealRegression()

• 普通最小二乘法线性回归
• coef_: 回归系数 （w值)

1. sklearn.linear_model.SGDRegressir()

• 通过使用SGD最小化线性模型
• coef_: 回归系数
• 不能手动指定学习率

波士顿房价预测

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error

def mylinear():
    """
    线性回归预测房价
    :return: None
    """
    # 1. 获取数据
    lb = load_boston()

    # 2. 分割数据集到训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
    print(y_train, y_test)

    # 3. 进行标准化处理(特征值和目标值都必须标准化处理）
    # 实例化两个标准化API,特征值和目标值要用各自fit
    # 特征值
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    std_y = StandardScaler()
    y_train = std_y.fit_transform(y_train)
    y_test = std_y.transform(y_test)

    # 4. estimator预测
    # 4.1 正规方程求解预测结果
    lr = LinearRegression()
    lr.fit(x_train, y_train)
    print(lr.coef_)
    y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
    print('正规方程测试集里面每个房子的预测价格：', y_lr_predict)
    print('正规方程的均方误差：',mean_squared_error(std_y.inverse_transform(y_test),y_lr_predict))

    # 4.1 梯度下降进行梯度预测
    sgd = SGDRegressor()
    lr.fit(x_train, y_train)
    print(sgd.coef_)
    y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
    print('梯度下降测试集里面每个房子的预测价格：', y_sgd_predict)
    print('梯度下降的均方误差：', mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
    return None


if __name__ == '__main__':
    mylinear()

回归性能评估

均方误差 （Mean Squared Error MSE) 评价机制

• mean_squared_error(y_true, y_pred)
• 真实值和预测值为标准化话之前的值
  

两种预测方式的选择

1. 样本量选择
   样本量大于100K --> SGD 梯度下降
   样本量小于100K --> 其他

梯度下降	正规方程
需要选择学习率	不需要
需要多次迭代	一次运算得出
当特征数量大时也能较好使用	需要计算（xTx）-1,运算量大
适用于各种类型的模型	只适用于线性模型

1. 特点：线性回归器是最为简单、易用的回归模型，在不知道特征之间关系的情况下，
   可以使用线性回归器作为大多数系统的首要选择。LinearRegression 不能解决拟合问题。

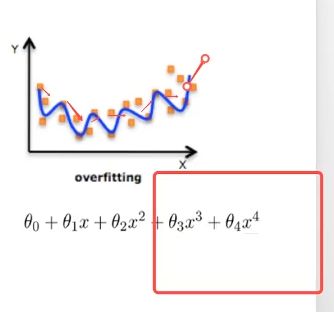
过拟合与欠拟合

1. 定义：

   1. 过拟合（overfitting)：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在训练数据外却不能很好拟合。（模型过于复杂）
      模型复杂的原因： 数据的特征和目标值之间的关系不仅仅是线性关系。

   2. 欠拟合（underfitting)：一个假设在训练数据上不能获得更好的拟合，但是在训练数据外也不能很好的拟合。 （模型过于简单）
      

欠拟合原因及解决方法

1. 原因： 学习到的数据特征过少
2. 解决方法： 增加数据的特征数量

过拟合原因及解决方法

1. 原因： 原始特征过多，存在一些嘈杂特征，模型过于复杂是因为模型尝试去兼顾各个测试数据点
2. 解决方法：
   • 进行特征选择，消除关联性很大的特征（人为排除，很难做）
   • 交叉验证（让所有数据都有过训练）- 检验但不能解决
   • 正则化 ：不断尝试，减少权重（高次项特征的影响）
3. 特征选择：
   • 过滤式：低方差特征
   • 嵌入式：正则化，决策树，神经网络
     

（减少高指数项系数，趋近于0，减少权重）

L2正则化

1. 作用：可以使得W的每个元素都很小，都接近于0
2. 优点：越小的参数说明模型越简单，越简单的模型越不容易产生过拟合现象。
3. 回归解决过拟合的方式：
   L2正则化， Ridge：岭回归：带有正则化的线性回归，解决过拟合。

Ridge API

sklearn.linear_model.Ridge(alpha=1.0)
- 具有L2正则化的线性最小二乘法
- alpha: 正则化力度 0~1（小数）， 1~10（整数）
- coef_: 回归系数

正则化力度对权重的影响 （力度越大，越趋向于0）

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error

def mylinear():
    """
    线性回归预测房价
    :return: None
    """
    # 1. 获取数据
    lb = load_boston()

    # 2. 分割数据集到训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
    print(y_train, y_test)

    # 3. 进行标准化处理(特征值和目标值都必须标准化处理）
    # 实例化两个标准化API,特征值和目标值要用各自fit
    # 特征值
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    std_y = StandardScaler()
    y_train = std_y.fit_transform(y_train)
    y_test = std_y.transform(y_test)

    # 4. estimator预测
    # 4.1 正规方程求解预测结果
    lr = LinearRegression()
    lr.fit(x_train, y_train)
    print(lr.coef_)
    y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
    print('正规方程测试集里面每个房子的预测价格：', y_lr_predict)
    print('正规方程的均方误差：',mean_squared_error(std_y.inverse_transform(y_test),y_lr_predict))

    # 4.2 梯度下降进行梯度预测
    sgd = SGDRegressor()
    lr.fit(x_train, y_train)
    print(sgd.coef_)
    y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
    print('梯度下降测试集里面每个房子的预测价格：', y_sgd_predict)
    print('梯度下降的均方误差：', mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))

    # 4.3 岭回归预测
    rd = Ridge(alpha=1.0)
    rd.fit(x_train, y_train)
    print(rd.coef_)
    y_rd_predict = std_y.inverse_transform(rd.predict(x_test))
    print('岭回归测试集里面每个房子的预测价格：', y_rd_predict)
    print('岭回归的均方误差：', mean_squared_error(std_y.inverse_transform(y_test), y_rd_predict))


    return None


if __name__ == '__main__':
    mylinear()

线性回归LinearRegression 与 Ridge对比

岭回归：回归得到的回归系数更符合实际，更可靠。另外，能让估计参数的波动范围变小，变得更稳定。在存在病态数据偏多的研究中有较大的使用价值。

模型的保存与加载

sklearn API
sklearn.Externals import joblib

• 保存： joblib.dump(rf, 'test.pkl') - 保存的实例和路径 ， rf - 训练生成的实例，文件格式为pkl
• 加载： joblib.load( 'test.pkl') - 加载路径

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
from sklearn.externals import joblib

def mylinear():
    """
    线性回归预测房价
    :return: None
    """
    # 1. 获取数据
    lb = load_boston()

    # 2. 分割数据集到训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
    print(y_train, y_test)

    # 3. 进行标准化处理(特征值和目标值都必须标准化处理）
    # 实例化两个标准化API,特征值和目标值要用各自fit
    # 特征值
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    std_y = StandardScaler()
    y_train = std_y.fit_transform(y_train)
    y_test = std_y.transform(y_test)

    # 4. estimator预测
    # 4.1 正规方程求解预测结果
    # lr = LinearRegression()
    # lr.fit(x_train, y_train)
    # print(lr.coef_)
    # y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
    # print('正规方程测试集里面每个房子的预测价格：', y_lr_predict)
    # print('正规方程的均方误差：',mean_squared_error(std_y.inverse_transform(y_test),y_lr_predict))

    # 保存训练好的模型
    joblib.dump(lr, './test.pkl')

    # 导出模型
    model = joblib.load('./test.pkl')
    y_predict = model.predict(x_test)
    print('保存的模型预测的结果：', y_predict)

    # # 4.2 梯度下降进行梯度预测
    # sgd = SGDRegressor()
    # lr.fit(x_train, y_train)
    # print(sgd.coef_)
    # y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
    # print('梯度下降测试集里面每个房子的预测价格：', y_sgd_predict)
    # print('梯度下降的均方误差：', mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
    #
    # # 4.3 岭回归预测
    # rd = Ridge(alpha=1.0)
    # rd.fit(x_train, y_train)
    # print(rd.coef_)
    # y_rd_predict = std_y.inverse_transform(rd.predict(x_test))
    # print('岭回归测试集里面每个房子的预测价格：', y_rd_predict)
    # print('岭回归的均方误差：', mean_squared_error(std_y.inverse_transform(y_test), y_rd_predict))


    return None


if __name__ == '__main__':
    mylinear()