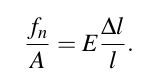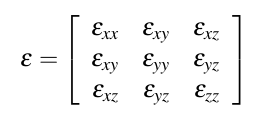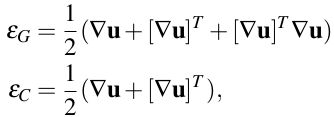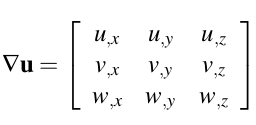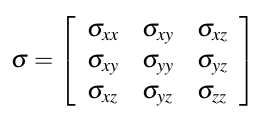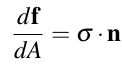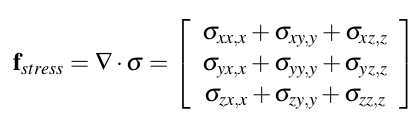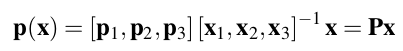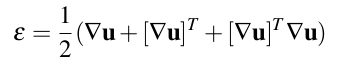简介
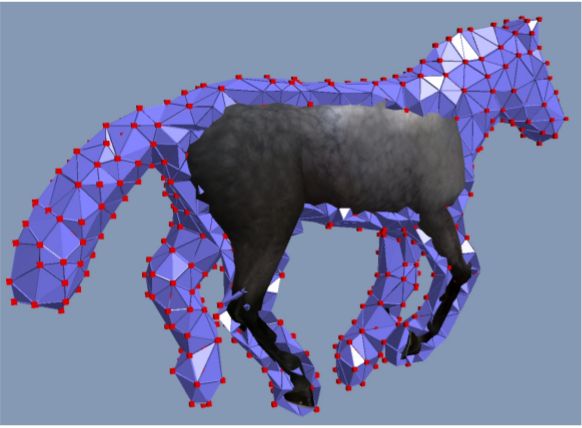
有限元法最初的概念源自用结构力学的方法解决弹性力学的问题,后来扩展到各种用微分方程描述的学科。最初的有限单元法多用于工程计算,随着计算机性能的不断增强以及对图形表现真实性的进一步需求,有限单元法也逐渐应用到了图形的领域。
连续介质力学 Continuum Mechanics
在图形学中,可变形的物体通常建模为连续介质的三维物体,其中最重要的三个量是:位移,应力,应变。
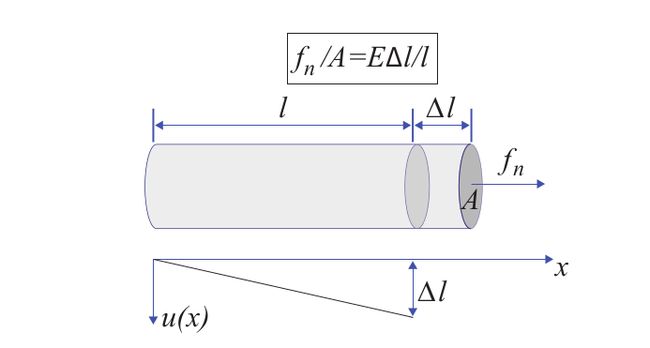
对于一维的情况,如下图:
由Hooke's law 很容易得到:
其中E是杨氏模量,描述的是材料的刚度。引入应力![]() 和应变
和应变![]() ,则式子可简化为:
,则式子可简化为:
下面来定义一些符号。
一个三维可变形物体主要由一个未变行状态的体(undeformed shape, rest shape,initial shape)和一些材料属性来定义.Rest shape为一个连续的三维空间子集,记为![]() ,其中的点
,其中的点![]() 称为点的材质坐标(material coordinates)。
称为点的材质坐标(material coordinates)。
当有力施加到rest shape 上的时候,x的位置移动到 p(x),因为 p(x) 定义为所有材质上的点,那么 p(x)为![]() 上的一个向量空间,记向量空间 u(x) = p(x) - x 为位移域(displacement field).
上的一个向量空间,记向量空间 u(x) = p(x) - x 为位移域(displacement field).
应变 Strain
为了在三维空间中使用Hooke 定律,需要用新的方法来表示。在大部分情况下,变形体内的应变都不是一样的。比如一个一端固定的悬臂梁,上侧是受拉,下侧则是受压。则应变其实是材料坐标的函数,记为![]() ,如果物体未发生形变,应变就是0,单纯的空间位移无法引起形变,所以应变也为0,因此应力其实是由位移域决定的。在三维空间中,位移域有三个部分:
,如果物体未发生形变,应变就是0,单纯的空间位移无法引起形变,所以应变也为0,因此应力其实是由位移域决定的。在三维空间中,位移域有三个部分:![]() ,每一个分量都可以对x,y,z方向微分。应变就不是一个单值了,这个非常重要,因为在一个三维物体中的一个点,可以在一个方向受压的同时,在另一个方向受拉。
,每一个分量都可以对x,y,z方向微分。应变就不是一个单值了,这个非常重要,因为在一个三维物体中的一个点,可以在一个方向受压的同时,在另一个方向受拉。
应变可以表示为一个 3*3 空间上的张量(tensor):
有两种从位移域计算应变张量的方法:
前者称为格林非线性应变张量,后者是科希线性应变张量。科希张量少了后面的二次部分,无法获取旋转量。位移域的梯度矩阵如下:
逗号后面的字母表示对其你偏导,求出梯度矩阵后很容易得到应变张量。
应力 Stress
应力指的是单位面积的受力,和应变一样,应力也可用一个3阶张量表示:
求得应力之后,想要求得某个面上的手里,则还需要知道这个面的法向,然后通过下面的公式求得:
本构关系
本构关系表示的应力和应变之间的关系。在三维空间中,Hooke 定律表示为:
在这里应力和应变都是3阶的张量,对与各向同性的材料(isotropic materials),Hooke 定律有:
这里的 v 是杨氏模量,取值范围是[0...1/2), 描述固体材料抵抗形变能力的物理量。
动力方程 Equation of Motion
将牛顿第二定律运用到弹性材料中的质点,有
![]()
由于我们不知道整个物体的质量,对与一个单位体积的立方体dxdydz,化为单位体积质量(也就是密度)的形式:
![]()
这里的 f(x) 指的是作用在x的 内力+外力合。
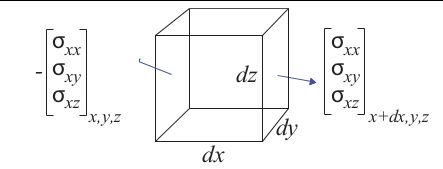
现在要做的是计算内力。对于一个变形体内的一个单位立方体dxdydz,垂直X方向的应力如下
应力是单位面积的力,则应力乘以面积就可以得到内力,再除以体积则得到x方向内力合为:
逗号表示 空间导数。
则由内部应力产生的内力合可表示为:
则完整的偏微分方程可以化为:
通过这个方程,我们就可以通过求出内力外力和,继而求出加速度,然后更新位置。
整理一下这个求解方法的pipeline:
1.密度和外力已知;
2.定义材料坐标 X 和世界坐标 P;
3.计算位移域 u =p-x;
4.计算位移域梯度,然后应变张量就可以获得(格林应变张量或者柯希应变张量);
5.根据Hooke's law 计算应力域;
6.根据牛顿第二定律计算出加速度;
7.利用显示或者隐式积分,更新P(x)。
这里还有两个概念需要说明一下。
材料线性:材料的应力和应变关系符合简单的Hooken law.(线性关系)
几何线性:应变张量使用的是柯希张量。
材料线性+集合线性得到的结果是动力学偏微分方程线性,偏微分方程线性的好处就是好求解。在deformate object 模拟中,大部分都是假设成线性的,这样能够使计算简单,获得更快的计算速度,但是对于大变形或者旋转,集合上的线性简化会引起一些很怪异的现象,这在后面会介绍一些解决的方法。
有限单元离散
在上面得到的偏微分方程中,p是一个连续向量空间,怎么描述物体中点位移会非常困难,因为物体有无限的质点,而我们需要求解解析解。
有一个方法可以无限近似的方式逼近真实解,这个方法的核心思想就是Finite Element Method(FEM),在力学中称为有限单元法。通过一些算法,将deformate object 的体mesh化分为网格单元mesh,网格单元之间不会有重叠,对于每一个单元,向量空间都可以根据单元顶点的位置写出解析式。
网格剖分的相关的文章:专注网格剖分 - TetGen,NETGEN,Steller
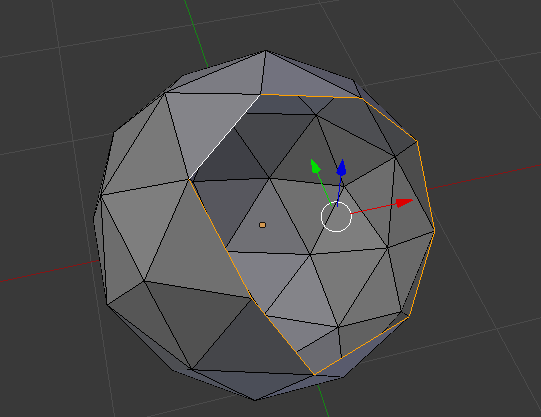
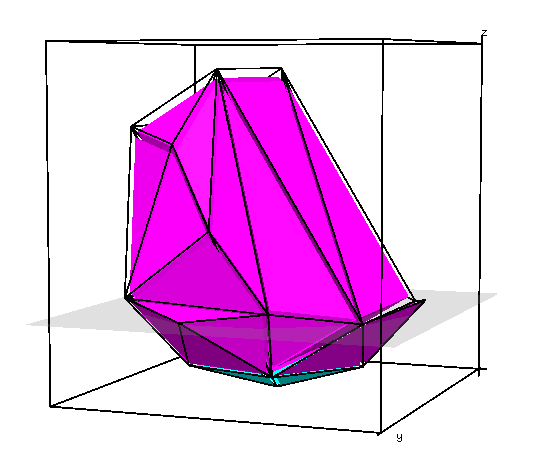
一个球体剖分的例子:
剖分后:
常应变四面体网格 Constant Strain Tetrahedral Meshes
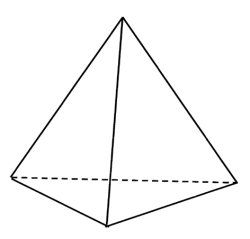
在有限单元法中,最简单的方法就是用四面体作为有限单元,这样的网格mesh称为四面体mesh。
在单元中,如果形变域为一个常量的话会更加简单,但是这样会导致应力为0,然后就无法模拟变形物体了。
对于如上图的一个四面体单元,x0,x1,x2,x3是在完全不受外力情况下的位置(rest shape),在形变状态下的位置为p0,p1,p2,p3,单纯的平移变换并不会产生内力,所以假设x0 = p0 = 0;
对与四面体中的某一点x,可以用重心坐标插值来表示:
变形之后,这一点的重心坐标是不变的,可以记为:
![]()
两式连立,消去b,得到
这是一个线性关系,[x1,x2.x3]矩阵的逆可以事先求出。
由于p(x)是线性的,所以有
又位移域 u = p-x,则
![]()
使用格林应变张量
再利用Hooken law,求出应力,然后乘以面积就可以得到内力。
例如,对于面(0,1,2)面上方的力如下:
三角形的两个向量叉乘得到三角形的面积。
最后,我们只要吧面力离散到三角形的各个顶点就可以了。
就如我们看到的,整个过程都非常简单,只是根据之前的一个状态不断地去计算各种变量,同时我们可以很轻易的将Hooken law 替换成其他的非线性模型。
下面给出整个模拟过程的伪代码.
一行行解释。
1-4:对有限元mesh中的所有单元进行初始化,初始位移和rest shape重合。
5-7:预处理每个单元的Xi;
8-11:这里开始主模拟循环。每次循环开始都要重新设置顶点上的力,初始设置为外力和;
13-14:计算出位移梯度;
15-16:用格林应变张量计算出应力;
17-22:计算单元中每个面上的力,然后将力离散到面上的每一个顶点;
24-26:到这一步,单元上的上的每一个顶点上的力都已经搞定了,接下来是更新每个点的位置;
28:更新显示。
算法的流程很像Mass - Spring - System. 虽然力的计算很耗时,但算法并没有因此更难理解或实现。
对于更稳定的模拟,一定要使用隐式积分。
参考
SIGGRAPH 2008 Course - Real Time Physics Class Notes
SIGGRAPH 2012 Course - FEM Simulation of 3D Deformable Solids: A practitioner’s guide to theory, discretization and model reduction