2019QM大作业2-weyl半金属Landau Level

说明 for cnblog

转载请注明出处：https://www.cnblogs.com/bllovetx/p/11874707.html
欢迎访问My Home Page
--2019.11.21

本文为作者2019年11月16日晚提交的南京大学量子力学大作业2，共享于本blog
希望能分享一下自己的想法！
另cnblog不能直接上传矢量图，为节省时间，blog上使用jpg代替
——2019.11.16与南雍山下

QM大作业2——weyl半金属的Landau Level

by 曾许曌秋 181240004
南京大学匡亚明学院大二数理
2019.11

---

\(\boldsymbol{Abstract}\)

本文利用给出的weyl半金属的哈密顿量求解了其在z方向均匀磁场中的本征态和本征值问题，即Landau Level，求解时，没有采用照搬经典Landau Level的求解办法（利用产生湮灭算符等方法，如参考文献[1]），而是利用其哈密顿量的特殊性，以及证明的算符和其平方的本征值和本征态的关系，直接转化为经典Landau Level问题，并进行了一些讨论。
该方法看似使得哈密顿量丧失了一部分性质，但本文通过一系列讨论和计算，成功的恢复了包括特征值符号，特征态，手性，态密度等属性。

说明

• 本作业采用高斯单位制
• 考虑非相对论情况
• 本作业参考了NJU，UCSD等量子讲义
• 由于作者才疏学浅，尚不能保证以下全部内容的正确性
• 由于作者时间有限（期中考试以及二专的学习），很多讨论和扩展尚来不及完善和完成

Landau Level

不考虑电子自旋，采用Landau规范：
\[ \boldsymbol{A}=(0,x,0)B,\boldsymbol{B}=(0,0,1)B \tag{1-1} \]
带入电磁场哈密顿量：
\[ H=\frac{1}{2\mu}(\boldsymbol{p}-\frac{q}{c}\boldsymbol{A})^2+\boldsymbol{V} \tag{1-2} \]
考虑到\(p_y\)与\(x\)对易：
\[ H=\frac{p_z^2}{2\mu}+\frac{p_x^2}{2\mu}+\frac{1}{2\mu}(p_y+\frac{eB}{c}x)^2\\ =\frac{p_z^2}{2\mu}+\frac{p_x^2}{2\mu}+\frac{1}{2}\mu\frac{e^2B^2}{\mu^2c^2}(x+\frac{cp_y}{eB})^2 \tag{1-3} \]
取\(\text{CSCO}=\{H,p_z,p_y\}\)，令\(\omega=\frac{eb}{\mu c}\)，\(x_0=\frac{cp_y}{eB}\)，则转化为x方向的谐振子，故能级为：
\[ E_n=(n+\frac{1}{2})\hbar\omega+\frac{p_z^2}{2\mu}\\ (n=0,1,2...) \tag{1-4} \]
若考虑自旋则能极会split

自旋与pauli matrix

自旋是电子的内禀（intrinsic）属性，与外在的运动状态无关，对于上述经典的朗道能级，若考虑自旋，应在\(\text{CSCO}\)中额外加入\(\sigma_z\)。
在\(\sigma_z\)本征态下，可以使用pauli matrix来描述自旋：
\[ \textbf{I}=\begin{bmatrix}1&0\\0&1\end{bmatrix},S^2=\frac{3}{4}\hbar\textbf{I}\\ \sigma_x=\begin{bmatrix}0&1\\1&0\end{bmatrix},S_x=\frac{1}{2}\hbar\sigma_x\\ \sigma_y=\begin{bmatrix}0&i\\-i&0\end{bmatrix},S_y=\frac{1}{2}\hbar\sigma_y\\ \sigma_z=\begin{bmatrix}1&0\\0&-1\end{bmatrix},S_z=\frac{1}{2}\hbar\sigma_z\\ \tag{2-1} \]
==Mark==:这恰好是四元数四个基（差一个虚数单位），构成一个非交换环，由此有对易，反对易关系如下：
\[ [\sigma_\alpha,\sigma_\beta]=\epsilon_{\alpha\beta\gamma}2i\sigma_\gamma \tag{2-2} \]
\[ [\sigma_\alpha,\sigma_\beta]_+=2\delta_{\alpha\beta} \tag{2-3} \]

The Schrödinger-Pauli Hamiltonian

为考虑自旋，考虑如下哈密顿量：
\[ H=\frac{1}{2\mu}[\boldsymbol{\sigma}(\boldsymbol{p}+\frac{e}{c}\boldsymbol{A})]^2-e\phi \tag{3-1} \]
由于自旋是独立的物理量，与其他物理量显然都对易，利用上一节所述对易反对易关系，易将其展开：
\[ \begin{aligned}\ [\boldsymbol{\sigma}(\boldsymbol{p}+\frac{e}{c}\boldsymbol{A})]^2 &=\sigma_i\sigma_j[p_ip_j+\frac{e^2}{c^2}A_iA_j+\frac{e}{c}(p_iA_j+A_ip_j)]\\ &=\sigma_i\sigma_j[p_ip_j+\frac{e}{c}(A_ip_j+A_jp_i)+\frac{e^2}{c^2}A_iA_j+\frac{e\hbar}{ic}\frac{\partial A_j}{\partial x_i}]\\ &=\frac{1}{2}[\sigma_i,\sigma_j]_+[p_ip_j+\frac{e}{c}(A_ip_j+A_jp_i)+\frac{e^2}{c^2}A_iA_j]+(i\epsilon_{ijk}\sigma_k+\delta_{ij})\frac{e\hbar}{ic}\frac{\partial A_j}{\partial x_i}\\ &=[p_i^2+\frac{e}{c}(2A_ip_i+\frac{\hbar}{i}\frac{\partial A_i}{\partial x_i})+\frac{e^2}{c^2}A_i^2]+\frac{e\hbar}{c}(\epsilon_{ijk}\sigma_k\frac{\partial A_j}{\partial x_i})\\ &=(\boldsymbol{p}+\frac{e}{c}\boldsymbol{A})^2+\frac{e\hbar}{c}\boldsymbol{\sigma}\cdot(\nabla\times\boldsymbol{A}) \end{aligned} \tag{3-2} \]
即有：
\[ H=\frac{1}{2\mu}(\boldsymbol{p}+\frac{e}{c}\boldsymbol{A})^2+2\frac{e}{2\mu}(\frac{\hbar}{2}\boldsymbol{\sigma})\cdot\frac{\boldsymbol{B}}{c}-e\phi\tag{3-3} \]
这里可以看到明显的物理图像，同时，注意到自旋的g-factor=2

weyl 半金属的Landau Level

weyl半金属

由题，右手weyl半金属满足weyl方程，即其哈密度量为：
\[ H=v_F\boldsymbol{\sigma\cdot p}\tag{4-1} \]
其中\(v_F\)为费米速度，考虑到z方向的磁场，对（4-1）的哈密顿量做修正：
\[ H=v_F\boldsymbol{\sigma\cdot }(\boldsymbol{p}+\frac{e}{c}\boldsymbol{A})\tag{4-2} \]

从能量平方回到能量

注意到上述哈密顿量平方后恰好就是前文提到的Schrödinger-Pauli Hamiltonian，我们是否可以将weyl半金属恢复成普通的电子呢？
如若可以的话，就意味着我们可以将其直接转化为已解决的几个子问题！
下面我们将尝试在数学上证明这件事的可行性，即证明：

任何物理量\(A\),可以利用\(A^2\)的本征值和本征态，通过一定的操作反求\(A\)的本征态

证明如下：
将\(A\)视为一个矩阵，由\(A\)为物理量，一定可对角化，即其所有特征值（\(\lambda_1,\lambda_2,...\lambda_k\)）张成的子空间维度之和一定恰为A的阶数（也是\(A^2\)的阶数——双射）
这意味这，如果对任意\(i\neq j,|\lambda_i|\neq|\lambda_j|\)，则\(A^2\)的特征值与A的特征值一一对应，子空间完全相同，即\(H^2\)的特征向量和特征值也是\(H\)的特征值与特征向量。
唯一的反例出现在\(\lambda_i=-\lambda_j\)时，考虑一对互为相反数的\(A\)的特征值（\(\lambda_i=-\lambda_j\)），\(i,j\)子空间的矢量在\(A^2\)作用下本征值退化为同一个本征值\(|\lambda_i|\)，即对\(A^2\)而言，本征值\(|\lambda_i|\)的子空间恰好是\(\lambda_i\)子空间和\(\lambda_j\)子空间通过笛卡尔积张成的新的，维度为\(n_i+n_j\)的子空间，刚好也是双射，示意图如下：

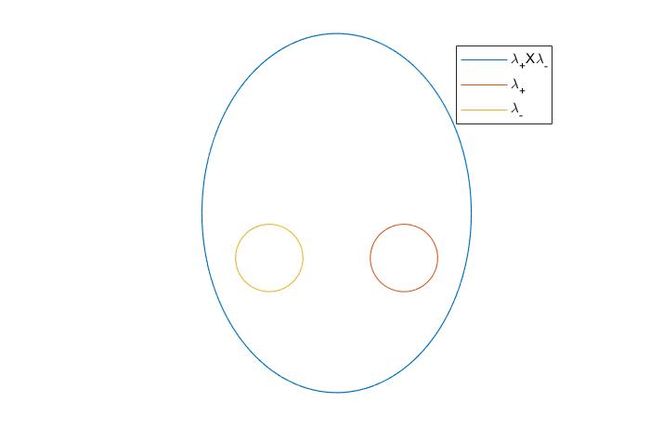
那么我们得到，\(A^2\)的特征值一定是\(A\)的某个特征值的平方，且若该特征值（指\(A\)的）不正负成对出现，则相应的特征态一一对应，否则（正负成对出现）\(A^2\)该特征值的子空间一定是\(A\)对应正负本征值对的子空间笛卡尔积张成的空间。 没有其他的本征值和本征态。

下面利用该性质，证明物理上总可以较为简洁的利用\(A^2\)的本征值和本征态反求出A的本征值和本征态。
若不正负成对，则对用本征态本征值直接相同。
若成对，则该本征态必然简并，这意味着总可以选一个物理量\(B\)，\(B\)与\(A^2\)对易却与\(A\)不对易，若取\(A^2\)和\(B\)的共同本征态（\(A^2\)本征值\(\lambda^2\)，对应\(A\)的本征值\(\lambda_+=\lambda=-\lambda_-\))，显然必不是\(A\)的本征态，但是根据上文，若设\(\lambda\)的本征态\(\boldsymbol{\alpha}\)，\(\lambda_+\)的本征态\(\boldsymbol{\alpha_+}\)，\(\lambda_-\)的本征态\(\boldsymbol{\alpha_-}\)（这里只证明正负各一个本征态，显然可推广），则必有：
\[ \left\{ \begin{aligned} \lambda\boldsymbol{\alpha}&=\lambda(k_+\boldsymbol{\alpha_+}+k_-\boldsymbol{\alpha_-})\\ A\boldsymbol{\alpha}&=\lambda(k_+\boldsymbol{\alpha_+}-k_-\boldsymbol{\alpha_-}) \end{aligned} \right. \tag{4-3} \]

从而有：
\[ \left\{ \begin{aligned} k_+\boldsymbol{\alpha_+}=\frac{(\lambda+A)}{2\lambda}\boldsymbol{\alpha}\\ k_-\boldsymbol{\alpha_-}=\frac{(\lambda-A)}{2\lambda}\boldsymbol{\alpha} \end{aligned} \right. \tag{4-4} \]
其中\(k_+,k_-\)仅为归一化系数。

右手weyl半金属Landau Level的转化求法

下面来解决哈密顿量的本征值问题，考虑到\(\boldsymbol{\sigma}\)是独立的物理量，直接求解也并不复杂，不过考虑到上文所提性质，我们直接求能量平方的本征值和本征态：
令算符：
\[ T=\frac{H^2}{2\mu v_F^2}=\frac{1}{2\mu}[\boldsymbol{\sigma}(\boldsymbol{p}+\frac{e}{c}\boldsymbol{A})]^2 \tag{4-5} \]
利用（3-1）和（3-3）可知：
\[ T=\frac{1}{2\mu}(\boldsymbol{p}+\frac{e}{c}\boldsymbol{A})^2+2\frac{e}{2\mu}(\frac{\hbar}{2}\boldsymbol{\sigma})\cdot\frac{\boldsymbol{B}}{c} \tag{4-6} \]
采用（1-1）Landau规范，再利用(1-3)
\[ T=\frac{p_z^2}{2\mu}+\frac{p_x^2}{2\mu}+\frac{1}{2}\mu\frac{e^2B^2}{\mu^2c^2}(x+\frac{cp_y}{eB})^2+2\frac{e}{2\mu}(\frac{\hbar}{2}\sigma_z)\cdot\frac{B}{c} \tag{4-7} \]
直接取\(\text{CSCO}=\{T,p_z,p_y,\sigma_z\}\),则有本征值和相应的本征态：
\[ \left\{ \begin{aligned} T&=\frac{p_z^2}{2\mu}+(n+\frac{1}{2})\hbar\omega+\frac{e\hbar B}{2\mu c}s_z\ (n=0,1,2...,s_z=\plusmn1)\\ |E_{ns}|&=v_F\sqrt{p_z^2+(n+\frac{1+s_z}{2})\frac{2eB\hbar}{c}}\\ \psi&=C\phi_n(x-x_0)exp(\frac{ip_y}{\hbar}y)exp(\frac{ip_z}{\hbar}z)\ |\ s_z>\ (x_0=-\frac{cp_y}{eB}) \end{aligned} \right. \tag{4-8} \]
其中\(\omega=\frac{eB}{\mu c}\)，\(s_z\)为z方向pauli算符本征值，|\(s_z\)>为相应本征态。考虑到：
\[ \boldsymbol{\sigma\cdot p}=\sigma_xp_x+\sigma_yp_y+\sigma_zp_z+\frac{eB}{c}\sigma_yx \tag{4-9} \]
可以注意到：
\[ \left\{ \begin{aligned} [\boldsymbol{\sigma\cdot p},p_z]&=0\\ [\boldsymbol{\sigma\cdot p},p_y]&=0\\ [\boldsymbol{\sigma\cdot p},\sigma_z]&=[\sigma_x,\sigma_z]p_x+[\sigma_y,\sigma_z]p_y+\frac{eBx}{c}[\sigma_y,\sigma_z] \\&=2i(\sigma_yp_x+\sigma_xp_y+\frac{eBx}{c}\sigma_x)\neq0 \end{aligned} \right. \tag{4-10} \]
任意\(T\)的本征态都符合上一小节讨论的要求（\(\sigma_z\)与\(H\)不对易），即\(H\)的所有本征值都应当正负成对出现（其实并不正确，见下文）。同时进一步将\(s_z\)视为n的一部分，则有：
\[ E_n=\plusmn v_f\sqrt{p_z^2+n\frac{2eB\hbar}{c}}\ n=0,1,2... \tag{4-11} \]
上式其实仍不正确!，因为有一个特例没有考虑，即当且仅当上式中的n取零时，由（4-8）：
\[ 0=n=n_{4-8}+\frac{1+s_z}{2}\\ if\ and\ only\ if:\\ s_z=-1 \tag{4-12} \]
对\(\sigma_z\)是非简并的(而其他都是二重简并，对应正负）！这意味着，由前面的讨论，对n=0，并非正负成对，而是只能取其一，那么究竟应该取正还是负？
这一点其实也是显然的，注意（4-9），对于\(n=0(n_{4-8}=0,s_z=-1)\)的情况，只有\(\sigma_zp_z\)项被保留，而上文一看到，改非简并态要取\(s_z=-1\)（自旋-z方向本征态）从而只\(\sigma_z\)为负，为体现简并性质，并考虑到n=0取负，我们将能量写成如下形式：
\[ (right)E_n= \left\{ \begin{aligned} &\frac{n}{|n|}v_F\sqrt{p_z^2+|n|\frac{2eB\hbar}{c}} &n&\in\boldsymbol{Z^*}\\ &-v_Fp_z &n&=0 \end{aligned} \right. \tag{4-13} \]

至于波函数直接套用（4-4）即可求出，由于时间关系且与讨论无关，这里不作具体计算。

态密度

下面求一下态密度。所谓态密度，指的是三维空间内，单位体积，（考虑到\(p_z\)能量实际可以连续取值）能量\(E\rightarrow E+dE,\frac{dn}{dE}\)。

%绘制时未保存jpg，待补充

如上图所示，考虑某一能量\(E\),即图中与\(p_z\)轴平行的红色直线。
所有可取的\(p_z\)即图中所有交点。考虑\(L_x\times L_y \times L_z\)的“箱”。
先考虑x-y平面，与Landau Level完全相同：
\[ \Delta p_y=\frac{2\pi\hbar}{L_y} \tag{4-14} \]
\[ n_{xy}=\frac{L_x}{\Delta x_0}=\frac{L_xL_yeB}{c2\pi\hbar} \tag{4-15} \]
接着考虑z方向，n=0必相交，且只有一个交点
\[ |\frac{dp_z}{\Delta p_zdE}|_{n=0}=\frac{L_z}{2\pi v_F\hbar} \tag{4-16} \]
对n>0，考虑到有两个交点，且截断，有：
\[ \begin{aligned} |2\frac{dp_z}{\Delta p_zdE}|_{n>0}&=2\frac{L_z}{2\pi\hbar}Re[|\frac{d\sqrt{(\frac{E}{v_F})^2-n\frac{2eB\hbar}{c}}}{dE}|]\\ &=2\frac{L_z}{2\pi\hbar v_F}Re[\frac{|E|}{\sqrt{(E)^2-n\frac{2eB\hbar}{c}v_F^2}}] \end{aligned} \tag{4-17} \]
综上，态密度为：
\[ \begin{aligned} D(E)&=\frac{1}{L_xL_yL_z}n_{xy}\sum_{n}n_z\\ &=\frac{eB}{c4\pi^2\hbar^2v_F}(1+\sum_{n=0}^\infin(2Re[\frac{|E|}{\sqrt{(E)^2-n\frac{2eB\hbar}{c}v_F^2}}])) \end{aligned} \tag{4-18} \]

左手weyl半金属

老师在课上曾提到，左手性weyl半金属的哈密顿量只要在乘手性即可，即：
\[ \begin{aligned} H_{left}&=v_F(\begin{bmatrix}1&0&0\\0&1&0\\0&0&-1\end{bmatrix}\cdot\boldsymbol{\sigma})\cdot\boldsymbol{p}\\ &=v_F(\sigma_xp_x+\sigma_yp_y-\sigma_zp_z+\frac{eB}{c}\sigma_yx) \end{aligned} \tag{4-19} \]
不妨看一下区别：
注意到（3-2）式中前半部分只有平方项，而后半部分的交叉相中，又当且仅当\(\frac{\partial A_j}{\partial x_i}\)中\(i,j\)中有一个取z时才可能有影响，而我们知道，磁场沿z轴时是绝对不会出现这种case的（对z轴求导的磁场不沿z方向，z轴均匀磁场的磁矢势与不显含z）故而\(T\)算符不受影响，能量本征值的平方也不受影响。仍有\(n=0(s_z=-1,n_{4-8}=0)\)对\(T\)非简并。
再看哈密顿量（4-19）对于n=0，进剩\(-v_F\sigma_zp_z\)项，由于提到的\(s_z=-1\)知：
\[ (left)E_n= \left\{ \begin{aligned} &\frac{n}{|n|}v_F\sqrt{p_z^2+|n|\frac{2eB\hbar}{c}} &n&\in\boldsymbol{Z^*}\\ &v_Fp_z &n&=0 \end{aligned} \right. \tag{4-20} \]

\(\boldsymbol{Discussion}\)

weyl半金属Landau Level与经典Landau Level对比

首先weyl半金属能级split，这里并非单指自旋，上课讨论的经典的Landau Level并未考虑自旋，加入自旋后同样会split，但是能量总是正的，而weyl半金属则出现（对\(n\neq0\)）正负成对的能级，其本质原因其实从本作业采取的计算方法可以有更深刻的理解，即正常金属的每一个能级的子空间被拆分成了两个“共轭”的子空间，能量恰为相反值。从这样的角度来看，这也是一种能级的split。
更重要的，由于谐振子的能级只能取遍半无限个整数域，必然造成了基态的特殊性，即无法split，且这一点是手性相关的（见下文讨论）
其二，经典的Landau Level，能级等间隔，且与z方向动能线性相关的，而weyl半金属则完全不同！
其能级按照\(\sqrt{n}\)增加，能级越高，间隔约小。更重要的一点，由于能量与z分量动能不成线性关系，这意味着z方向动能是能级相关的。
说的更明白一点，对于经典的Landau Level，z方向动能完全可以不考虑，是独立于其他能量的。而weyl半金属的能级表达式，意味着能级间隔等都会随z方向动能发生改变，换句话说就是色散。
最后，如前所述，由于考虑到z方向动量，实际能量是连续分布，参见前文态密度相关讨论

weyl半金属Landau Level物理图像

weyl半金属的手性（基态）的物理图像其实是很明显的，为抵消谐振子能量中的常数项，考虑到自旋在磁场中的表达式（要求磁矩与磁场反向才能抵消），以及电子电量为负，必须取自旋与磁场反向。
\[ -\boldsymbol{m}\cdot\boldsymbol{B}+\frac{1}{2}\hbar\omega=0 \tag{5-1} \]
其成立显然也依赖于电子自旋\(g_{factor}=2\)的事实
而所谓手性，按照参考论文的说法[2]，即自旋在动量方向的投影，正则为右手，负则为左手，从而上述对自旋的要求与右手动量正方向反向，与左手同向，从而造成了手性相关的差异。

手性Landau Level区别及其物理意义

上文我们看到左右手性当且仅当取最低（绝对值）能级时产生区别：
\[ E_n= \left\{ \begin{aligned} &\frac{n}{|n|}v_F\sqrt{p_z^2+|n|\frac{2eB\hbar}{c}} &n&\in\boldsymbol{Z^*}\\ &v_Fp_z &n&=0(left)\\ &-v_Fp_z &n&=0(rignt) \end{aligned} \right. \tag{5-2} \]
为了更清楚的体现能级变化以及随z方向动量变化的色散，不妨做出各能级随z方向动量变化曲线如下图

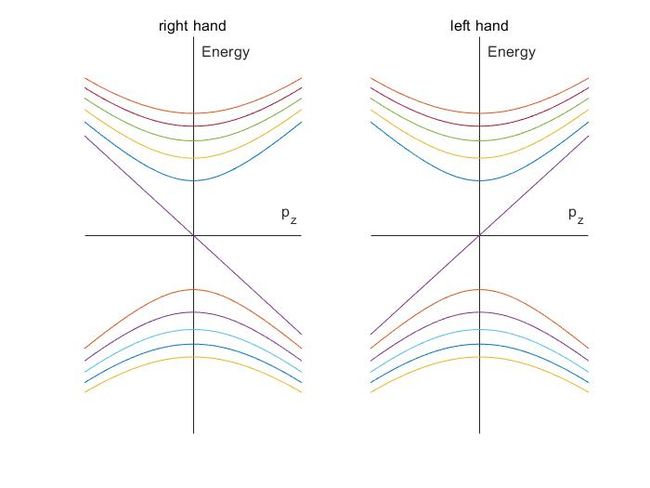
这样的手性差别会产生怎样的效应呢，可以看到，基态能量的不同造成能量相同的电子具有相反的动量（感觉有点像Hall效应的感觉）
其次，相关文献[3]中提到当电场与磁场同向时，电场会造成能级与z方向动量相图的偏移。基态能量的不同会造成态密度的不同，从而产生ABJ效应。

\(\boldsymbol{references}\)

[1]R. Rechciński,J. Tworzydło. Landau Levels of Double-Weyl Nodes in a Simple Lattice Model[J].ACTA PHYSICA POLONICA A,2016,130:1179-1182.doi:10.12693/APhysPolA.130.1179

[2]WAN Xian-Gang. Topological Weyl semimetals[J]. Physics,2015,44:427-438.doi:10.7693/wl20150702

[3]
Binghai Yan, Claudia Felser. Topological Materials:Weyl Semimetals. arXiv:1611.04182v2 [cond-mat.mtrl-sci] 21 Nov 2016