Erlang学习：尾递归

先来看一个简单的问题，输入一个数N，求出1+2+3+...+N。

这个问题可以使用循环解决

sum = 0;
for(i = 1; i <= N; i++)
           sum += i;

但是在函数式编程语言中，变量是不允许修改的，不能使用这样的循环，只能用递归。

先用C语言的递归实现求和

int sum(int N)
{
        if(N == 1)
              return 1;
        else
              return N + sum(N-1);
}

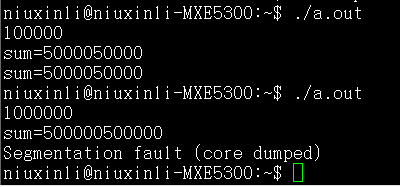
递归存在的一个普遍的问题就是栈溢出，尤其是像上面这个程序，N稍微大一点，堆栈就会溢出。看看下面代码的执行情况。

//iteration
long long sum1(long long x)
{
       long long i,sum=0;
      for(i = 1; i <= x; i++)
             sum += i;
      return sum;
}
//recursion
long long sum2(long long x)
{
       if(x == 1)
             return 1;
       else
            return x + sum2(x-1);
}
int main()
{
        long long x;
        scanf("%lld",&x);
        printf("sum=%lld\n",sum1(x));
        printf("sum=%lld\n",sum2(x));
}

可以看到，100000时栈还没溢出，到了1000000就不行了，使用迭代就不存在这个问题了。

既然递归存在这样的问题，而且函数式编程大量使用递归，那函数式编程岂不是一点优势也没有？

这就需要用到尾递归了。

int sum(int N)
{
        if(N == 1)
               return 1;
        else
              return N + sum(N-1);
}

我们来看一下这个函数，注意return N + sum(N-1)这条语句，假如调用到了sum(88)

执行 return 88 + sum(87)，sum(88)需要将88这个值放在栈里，等sum(87)返回了再使用88+sum(87)，因此sum(88)的栈不能被破坏，同样,87,86,85...,2，都需要保存在栈里，这样就容易造成栈的溢出。

现在修改一下上面的代码

int sum(int N)
{
         return sumX(0,N);
}
int sumX(int X, int N)
{
         if(N == 1)
                   return X + 1;
         else
                  return sumX(N+X, N-1);
}

还是以sum(88)为例，N就等于88，先调用sumX(0,88)，然后是sum(88,87)->sum(175,86)，这样我们把上层函数的状态都传给下面的函数，因此以前的栈可以破坏掉然后重新使用。这就是传说中的尾递归。不过即使使用了上面的代码，C语言编译器也不会为尾递归优化栈。

其实尾递归的本质就是，在函数最后，或者是递归结束条件，或者是仅调用函数，而不进行其它操作，比如return 1 + sum(x-1)，这就不是尾递归，因为调用了sum(x-1)后，又进行了一个加法操作。

在C语言层实现的尾递归并不会得到gcc的优化，我们可以手动修改汇编代码，实现一个真正的尾递归。但是要注意，不能优化成迭代了，必须满足一个条件，在函数里面调用自己。

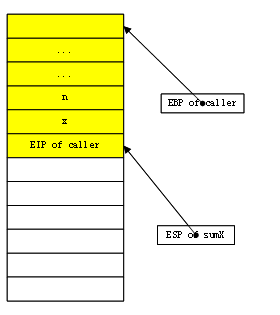
在sumX执行第一条语句时，栈格局如上图。

一般的情况，一个函数的头两句是

pushl %ebp

movl %esp, %ebp

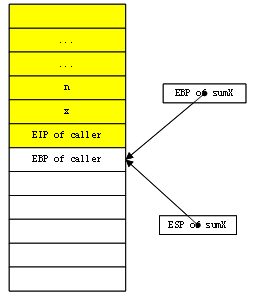
栈变成了这样：

为了实现尾递归，我们不再采用这种传统的函数调用方式。进入sumX后，不对ebp进行压栈。在里面再调用sumX时，不传递参数了，让它继续使用原来的参数。

判断n是否为1，如果为1，将x加1放入eax，返回。如果不为1，在原地将x加上n，将n-1，然后继续调用sumX。

sumX:
       cmpl $1,8(%esp)
       jne .next
       #如果n(也就是8(%esp))是1，那么将x(也就是4(%esp))放入eax中，加1，然后返回
       movl 4(%esp),%eax
       addl $1,%eax
       #返回
       pushl %ebp
       movl %esp,%ebp
       ret
.next:
       #将n加到x上
       movl 8(%esp),%eax
       addl %eax,4(%esp)
       #n-1
       subl $1,8(%esp)
       #这个call语句不会引起栈的增长
       call sumX

上面的代码存在一个问题，忘记了call时会将EIP压栈。

这就有问题了。第一次调用sumX时，需要将EIP压栈，但是第二次及以后就不能压栈了。用一个ugly的方法解决这个问题，若x=0，那么就是第一次，EIP需要压栈，否则在call之后将EIP再从栈里弹出来。

代码如下：

sumX:
     #先判断x是否为0，如果是，就将esp回移4个字节
     cmpl $0,4(%esp)
     je .fuck
     addl $4, %esp
.fuck
     cmpl $1,8(%esp)
     jne .next
     #如果n(也就是8(%esp))是1，那么将x(也就是4(%esp))放入eax中，加1，然后返回
     movl 4(%esp),%eax
     addl $1,%eax
     #返回
     pushl %ebp
     movl %esp,%ebp
     ret
.next:
     #将n加到x上
     movl 8(%esp),%eax
     addl %eax,4(%esp)
     #n-1
     subl $1,8(%esp)
     call sumX

 

 

老是容易忘   leave = movl %ebp,%esp  popl %ebp   ret = popl %eip  gdb十进制查看内存 x/u $esp + 4

 

在Erlang中，如果你写的程序是尾递归的，那么编译器会自动为你优化。

-module(sum).
-export([sum1/1,sum2/1]).

sum1(1)->1;
sum1(N)->
        N + sum1(N-1).

sum2(N)->
        sumx(0,N).

sumx(X,0)->
          X;
sumx(X,N)->
         sumx(N+X,N-1).

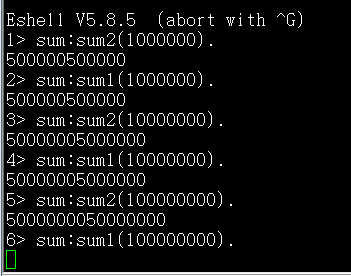
Erlang在递归10000000次时都不溢出，可见Erlang的栈设计的比C大多了，这是必须的，因为它是函数式编程语言。不过说到底，Erlang在普通的计算机上的栈是用堆模拟的，除非在Erlang的专用硬件上。

我用sum1时，内存耗光了，一直在swap。而sum2使用了尾递归，很快就计算出来了。