1.简介(只是简单介绍下理论内容帮助理解下面的代码,如果自己写代码实现此理论不够)
1) BP神经网络是一种多层网络算法,其核心是反向传播误差,即: 使用梯度下降法(或其他算法),通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。
BP神经网络模型拓扑结构包括输入层(input)、隐藏层(hidden layer)和输出层(output layer),每层包含多个神经元。
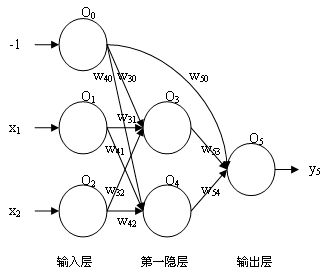
2)BP神经网络示例图
上图就是一个简单的三层BP神经网络。网络共有6个单元,O0用于表示阈值,O1、O2为输入层,O3、O4为第一隐层,也是唯一隐层,O5为输出层单元。网络接收两个输入![]() ,发送一个输出
,发送一个输出![]() 。每个单元接收一组输入,发送一个输出。
。每个单元接收一组输入,发送一个输出。![]() 为权值,例如W40 表示O0与O4之间的权重。
为权值,例如W40 表示O0与O4之间的权重。
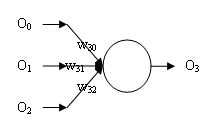
3)神经单元(计算单元)
如上图所示,每个圆表示一个神经单元。其接收一组数据,经过计算输出一个数据。
4)传播过程
a)正向传递
例如:从O1-->O4-->05,这是正向传递过程中的一个路径(O4除了接收O1,还接收O0、O2的输入)。这里重点说下权重,W41表示O1和O4之间的权重,假如O1=1,O4=4,W41=0.5,那么O5=1*4*0.5=2(2不是最终输出,最终输出还需要加上O0、O2 的计算结果).
b)反向传递(过程比较复杂,这个表述不是特别精确,只是为了方便理解)
例如:从O1<--O4<--05,在这个过程中,O5是计算出的值,参与计算的O4的值不是其本身的值,而是在正向传递过程中计算出的值(即输出值)。而权重也是这个过程中调整的。
2.MLPClassifier函数
此函数是sklearn.neural_network中的函数,它是利用反向传播误差进行计算的多层感知器算法。
a) 主要参数
hidden_layer_sizes:隐藏层,例如:(5,2) 表示有2个隐藏层,第一隐藏层有5个神经单元,第二个隐藏层有2个神经单元;(5,2,4)表示有三个隐藏层。
activation:激活函数,在反向传递中需要用到。有以下四个可选项:
'identity':无激活操作,有助于实现线性瓶颈, 返回 f(x) = x
'logistic':逻辑函数, 返回 f(x) = 1 / (1 + exp(-x)).
'tanh': 双曲线函数, 返回 f(x) = tanh(x).
'relu': 矫正线性函数, 返回 f(x) = max(0, x),(默认)
solver:反向传播过程中采用的算法,有以下三个选项:
'lbfgs': 准牛顿算法.适用于较小数据集
'sgd': 随机梯度下降算法.
'adam':优化的随机梯度下降算法(默认)。适用于较大数据集
alpha:L2惩罚系数
learning_rate:学习速率,有以下几个选项:(只有当slver='sgd'时有用)
constant:参数learning_rate_init指定的恒定学习速率.(默认选项)
invscaling’:使用“scale_t”的反向缩放指数逐渐降低每个时间步长t 的学习率。effective_learning_rate = learning_rate_init / pow(t,power_t)(power_t是另外一个参数)
adaptive: 自适应,只要损失不断下降就是用learning_rate_init。否则会自动调整(由另外一个参数tol决定)。
learning_rate_init:初始学习速率
b)属性
coefs_:权重列表
n_layers_:神经网络的总层数
3.示例一
本示例使用的数据:机器学习:从编程的角度去理解逻辑回归 。在下面的参数情况下正确率95%。
import numpy as np import os import pandas as pd from sklearn.neural_network import MLPClassifier def loadDataSet(): ##运行脚本所在目录 base_dir=os.getcwd() ##记得添加header=None,否则会把第一行当作头 data=pd.read_table(base_dir+r"\lr.txt",header=None) ##dataLen行dataWid列 :返回值是dataLen=100 dataWid=3 dataLen,dataWid = data.shape ##训练数据集 xList = [] ##标签数据集 lables = [] ##读取数据 for i in range(dataLen): row = data.values[i] xList.append(row[0:dataWid-1]) lables.append(row[-1]) return xList,lables def GetResult(): dataMat,labelMat=loadDataSet() clf = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=(5,2), random_state=1) clf.fit(dataMat, labelMat) #print("层数----------------------") #print(clf.n_layers_) #print("权重----------------------") #for cf in clf.coefs_: # print(cf) #print("预测值----------------------") y_pred=clf.predict(dataMat) m = len(y_pred) ##分错4个 t = 0 f = 0 for i in range(m): if y_pred[i] ==labelMat[i]: t += 1 else : f += 1 print("正确:"+str(t)) print("错误:"+str(f)) if __name__=='__main__': GetResult()
4.示例二(数据来源)
这次使用的数据还是红酒。因为红酒的口感得分是整数,所以也可以当作是分类。但是针对此实验数据,在多次调整参数的过程中(主要是调整隐藏层)正确率最高只有61%。这正是BP神经网络的一个缺陷:隐含层的选取缺乏理论的指导。
代码:
import numpy as np import os import pandas as pd from sklearn.neural_network import MLPClassifier ##运行脚本所在目录 base_dir=os.getcwd() ##记得添加header=None,否则会把第一行当作头 data=pd.read_table(base_dir+r"\wine.txt",header=None,sep=';') ##dataLen行dataWid列 :返回值是dataLen=1599 dataWid=12 dataLen,dataWid = data.shape ##训练数据集 xList = [] ##标签数据集 lables = [] ##读取数据 for i in range(dataLen): row = data.values[i] xList.append(row[0:dataWid-1]) lables.append(row[-1]) ##设置训练函数 clf = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=(14,14,30), random_state=1) ##开始训练数据
clf.fit(xList, lables) ##读取预测值 y_pred=clf.predict(xList) m = len(y_pred) t = 0 f = 0 ##预测结果分析 for i in range(m): if int(y_pred[i]) == lables[i]: t += 1 else : f += 1 print("正确:"+str(t)) print("错误:"+str(f))
5.BP神经网络的缺点
1)容易形成局部极小值而得不到全局最优值。BP神经网络中极小值比较多,所以很容易陷入局部极小值,这就要求对初始权值和阀值有要求,要使得初始权值和阀值随机性足够好,可以多次随机来实现。
2)训练次数多使得学习效率低,收敛速度慢。
3)隐含层的选取缺乏理论的指导。
4)训练时学习新样本有遗忘旧样本的趋势。(可以把最优的权重记录下来)