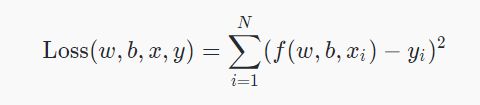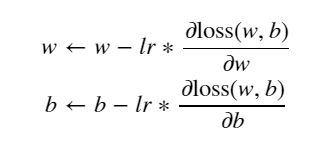实验一 TensorFlow 2.0 新增变化特性以及实验
介绍
TensorFlow 2.0 版本现已推出,相对于 1.x 版本在很多地方都有较大的变动。本次实验中,我们将了解并学习 TensorFlow 2.0 的一些新的特征,同时熟悉一些常用的新 API 方法。
知识点
安装 TensorFlow 2.0
Eager Execution
TensorFlow Keras
#### 学习此课程的前提是已了解并使用过 TensorFlow 1.x。
2019 年初,TensorFlow 官方推出了 2.0 预览版本,也意味着 TensorFlow 即将从 1.x 过度到 2.x 时代。根据 TensorFlow 官方介绍内容 显示,2.0 版本将专注于简洁性和易用性的改善,主要升级方向包括:
使用 Keras 和 Eager Execution 轻松构建模型。
在任意平台上实现稳健的生产环境模型部署。
为研究提供强大的实验工具。
通过清理废弃的 API 和减少重复来简化 API。
TensorFlow 2.0 安装
本人之前已经在自己电脑上安装了tensorflow-2.0.0版本,输入以下代码查看版本号。
import tensorflow as tf
tf._versionEager Execution
TensorFlow 2.0 带来的最大改变之一是将 1.x 的 Graph Execution(图与会话机制)更改为 Eager Execution(动态图机制)。在 1.x 版本中,低级别 TensorFlow API 首先需要定义数据流图,然后再创建 TensorFlow 会话,这一点在 2.0 中被完全舍弃。
TensorFlow 2.0 中的 Eager Execution 是一种命令式编程环境,可立即评估操作,无需构建图:操作会返回具体的值,而不是构建以后再运行的计算图。实际上,Eager Execution 在 1.x 的后期版本中也存在,但需要单独执行tf.enable_eager_execution() 进行手动启用。不过,2.0 版本的 TensorFlow 默认采用了 Eager Execution,无法关闭并回到 1.x 的 Graph Execution 模式中。
在之前1.x 版本中,如果我们新建一个张量 tf.Variable([[1, 2], [3, 4]]) 并执行输出,那么只能看到这个张量的形状和属性,并不能直接输出其数值。
如今,Eager Execution 模式下则可以直接输出张量的数值了,并以 NumPy 数组方式呈现。

Eager Execution 带来的好处是不再需要手动管理图和会话。例如,现在使用示例张量进行数学计算,可以像 Python 一样直接相加
相对于下面1.x的代码,是一个质的飞跃
init_op = tf.global_variables_initializer() # 初始化全局变量
with tf.Session() as sess: # 启动会话
sess.run(init_op)
print(sess.run(c + c)) # 执行计算TensorFlow 的默认执行模式为 Eager Execution,这就意味着之前基于 Graph Execution 构建的代码将完全无法使用,因为 2.0 中已经没有了相应的 API。例如,先前构建神经网络计算图时,都习惯于使用 tf.placeholder 占位符张量,等最终执行时再传入数据。Eager Execution 模式下,tf.placeholder 已无存在必要,所以此 API 已被移除。
所以,随着 TensorFlow 2.0 默认引入 Eager Execution 机制,也就意味着原 1.x 低阶 API 构建图的方法后续已无法使用。怪不得我之前的代码都报错,运行在1.x上没问题,运行到2.0.0上就各种错误,改变确实太大了,图与会话机制都有了改变。
实验总结
本次实验主要对 TensorFlow 2.0 新特征做了介绍和说明,并使用实例对比了 1.x 和 2.0 的不同之处。TensorFlow 2.0 的变化实际上是非常之大的,你会发现一些原先熟悉的 API 完全消失了,先前构建的代码也无法正常执行。这就需要花时间熟悉新的 API,并掌握新的模型构建流程。
TensorFlow Keras
TensorFlow 1.x 中,我们可以通过 tf.layers 高阶层封装开快速搭建神经网络。如果,2.0 已完全移除了 tf.layers 模块,转而引入了 tf.keras。
实验二 TensorFlow 2.0 实现线性回归
介绍
以线性回归为例,使用 TensorFlow 2.0 提供的 API 来进行实现。与此同时,我们会使用 1.x API 与之对比。
知识点
- 低阶 API 实现
- 高阶 API 实现
- TensorFlow 1.x 实现
低阶 API 实现
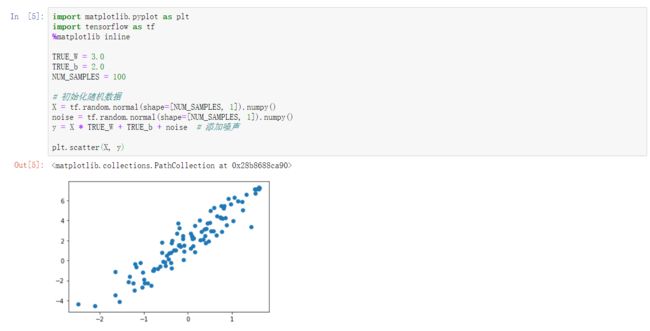
低阶 API 实现,实际上就是利用 Eager Execution 机制来完成。实验首先初始化一组随机数据样本,并添加噪声,然后将其可视化出来。
import matplotlib.pyplot as plt
import tensorflow as tf
%matplotlib inline
TRUE_W = 3.0
TRUE_b = 2.0
NUM_SAMPLES = 100
#初始化随机数据
X = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()
noise = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()
y = X * TRUE_W + TRUE_b + noise # 添加噪声
plt.scatter(X, y)利用线性函数去拟合,首先初始化w和b。
class Model(object):
def __init__(self):
self.W = tf.Variable(tf.random.uniform([1])) # 随机初始化参数
self.b = tf.Variable(tf.random.uniform([1]))
def __call__(self, x):
return self.W * x + self.b # w*x + b平方差损失函数的使用
def loss_fn(model, x, y):
y_ = model(x)
return tf.reduce_mean(tf.square(y_ - y))基础的梯度下降法
代码如下
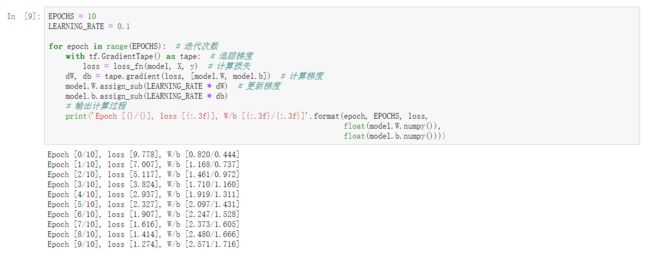
EPOCHS = 10
LEARNING_RATE = 0.1
for epoch in range(EPOCHS): # 迭代次数
with tf.GradientTape() as tape: # 追踪梯度
loss = loss_fn(model, X, y) # 计算损失
dW, db = tape.gradient(loss, [model.W, model.b]) # 计算w、b的梯度
model.W.assign_sub(LEARNING_RATE * dW) # 更新梯度
model.b.assign_sub(LEARNING_RATE * db)
# 输出计算过程
print('Epoch [{}/{}], loss [{:.3f}], W/b [{:.3f}/{:.3f}]'.format(epoch, EPOCHS, loss,
float(model.W.numpy()),
float(model.b.numpy())))
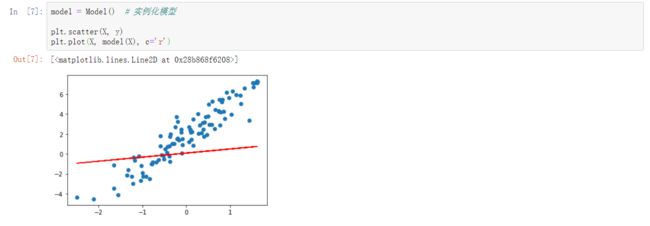
重新拟合
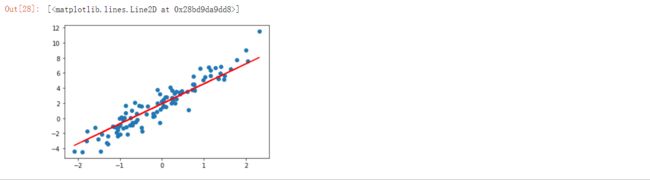
plt.scatter(X, y)
plt.plot(X, model(X), c='r')高阶 API 实现
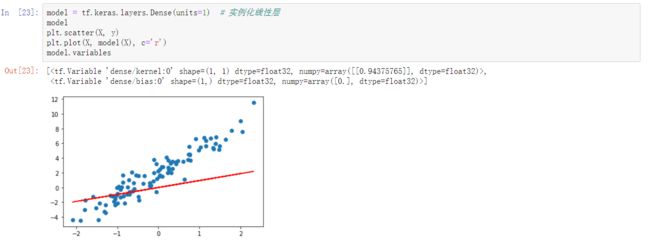
tf.keras 模块下提供的 tf.keras.layers.Dense 全连接层(线性层)实际上就是一个线性计算过程。所以,模型的定义部分我们就可以直接实例化一个全连接层即可。
model = tf.keras.layers.Dense(units=1) # 实例化线性层
model
#units 为输出空间维度。此时,参数已经被初始化了,所以我们可以绘制出拟合直线。
plt.scatter(X, y)
plt.plot(X, model(X), c='r')
model.variables#打印随机参数构建模型迭代过程
EPOCHS = 10
LEARNING_RATE = 0.002
for epoch in range(EPOCHS): # 迭代次数
with tf.GradientTape() as tape: # 追踪梯度
y_ = model(X)
loss = tf.reduce_sum(tf.keras.losses.mean_squared_error(y, y_)) # 计算损失
grads = tape.gradient(loss, model.variables) # 计算梯度
optimizer = tf.keras.optimizers.SGD(LEARNING_RATE) # 随机梯度下降
optimizer.apply_gradients(zip(grads, model.variables)) # 更新梯度
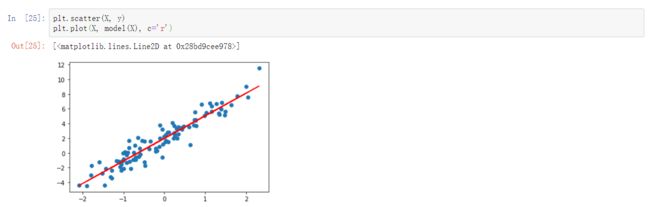
print('Epoch [{}/{}], loss [{:.3f}]'.format(epoch, EPOCHS, loss))重新拟合直线
plt.scatter(X, y)
plt.plot(X, model(X), c='r')Keras 方式实现
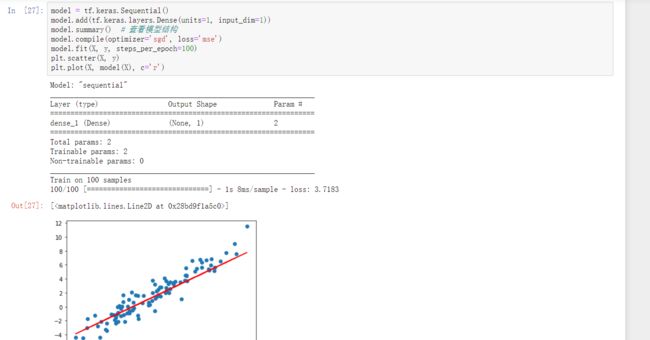
我们这里使用 Keras 提供的 Sequential 序贯模型结构。和上面的例子相似,向其中添加一个线性层。不同的地方在于,Keras 序贯模型第一层为线性层时,规定需指定输入维度,这里为 input_dim=1。
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(units=1, input_dim=1))
model.summary() # 查看模型结构
model.compile(optimizer='sgd', loss='mse')
model.fit(X, y, steps_per_epoch=100)
plt.scatter(X, y)
plt.plot(X, model(X), c='r')在tensorflow2.0版本下运行1.x版本
我们需要实验 TensorFlow 2.0 中 tensorflow.compat.v1 模块下提供的兼容性代码。
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior() # 关闭 Eager Execution 特性实验总结
本次实验中,我们利用 TensorFlow 2.0 提供的 Eager Execution 实现了线性回归的经典过程。同时,利用 TensorFlow Keras 高阶 API 简化了实现步骤。实验的最后,使用 TensorFlow 1.x API 进行了对比示例,准确把握 TensorFlow 2.0 和 1.0 之间的区别。
实验三 TensorFlow 2.0 构建神经网络
介绍
前面,我们以线性回归作为例子演示了 TensorFlow 2.0 的新变化和新特性。实际上,TensorFlow 等深度学习框架更重要的作用是用于构建人工神经网络。所以,本次实验将利用 TensorFlow 2.0 来构建一个简单的前馈神经网络。
知识点
低阶 API 构建
Keras 高阶 API 实现
低阶 API 构建--以手写数字识别为例
import numpy as np
import tensorflow as tf
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
digits = load_digits()
digits_y = np.eye(10)[digits.target.reshape(-1)] # 标签独热编码
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits_y,
test_size=0.2, random_state=1)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
class Model(object):
def __init__(self):
self.W1 = tf.Variable(tf.random.normal([64, 30])) # 随机初始化张量参数
self.b1 = tf.Variable(tf.random.normal([30]))
self.W2 = tf.Variable(tf.random.normal([30, 10]))
self.b2 = tf.Variable(tf.random.normal([10]))
def __call__(self, x):
x = tf.cast(x, tf.float32) # 转换输入数据类型
# 线性计算 + RELU 激活
fc1 = tf.nn.relu(tf.add(tf.matmul(x, self.W1), self.b1))
fc2 = tf.add(tf.matmul(fc1, self.W2), self.b2)
return fc2
def loss_fn(model, x, y):
preds = model(x)
return tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=preds, labels=y))
def accuracy_fn(logits, labels):
preds = tf.argmax(logits, axis=1) # 取值最大的索引,正好对应字符标签
labels = tf.argmax(labels, axis=1)
return tf.reduce_mean(tf.cast(tf.equal(preds, labels), tf.float32))
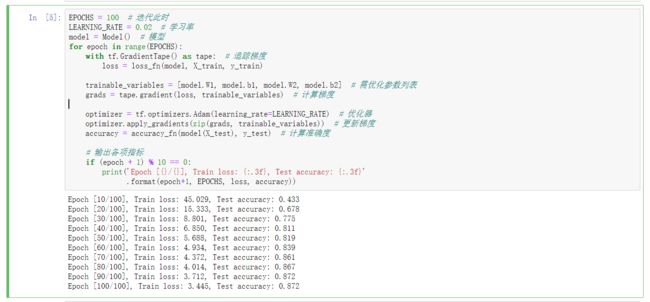
EPOCHS = 100 # 迭代此时
LEARNING_RATE = 0.02 # 学习率
model = Model() # 模型
for epoch in range(EPOCHS):
with tf.GradientTape() as tape: # 追踪梯度
loss = loss_fn(model, X_train, y_train)
trainable_variables = [model.W1, model.b1, model.W2, model.b2] # 需优化参数列表
grads = tape.gradient(loss, trainable_variables) # 计算梯度
optimizer = tf.optimizers.Adam(learning_rate=LEARNING_RATE) # 优化器
optimizer.apply_gradients(zip(grads, trainable_variables)) # 更新梯度
accuracy = accuracy_fn(model(X_test), y_test) # 计算准确度
# 输出各项指标
if (epoch + 1) % 10 == 0:
print('Epoch [{}/{}], Train loss: {:.3f}, Test accuracy: {:.3f}'
.format(epoch+1, EPOCHS, loss, accuracy))Keras 高阶 API 实现
函数式模型
inputs = tf.keras.Input(shape=(64,))
x = tf.keras.layers.Dense(30, activation='relu')(inputs)
outputs = tf.keras.layers.Dense(10, activation='softmax')(x)
#指定输入和输出
model = tf.keras.Model(inputs=inputs, outputs=outputs)
model.summary() # 查看模型结构
# 编译模型
model.compile(optimizer=tf.optimizers.Adam(),
loss=tf.losses.categorical_crossentropy, metrics=['accuracy'])
#训练和评估
model.fit(X_train, y_train, batch_size=64, epochs=10,
validation_data=(X_test, y_test))
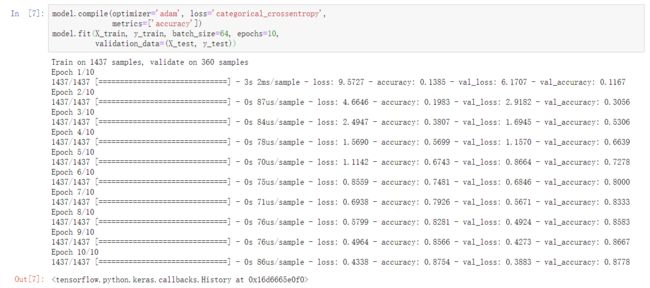
序贯模型
model = tf.keras.Sequential() # 建立序贯模型
model.add(tf.keras.layers.Dense(units=30, input_dim=64, activation='relu')) # 隐含层
model.add(tf.keras.layers.Dense(units=10, activation='softmax')) # 输出层
model.summary() # 查看模型结构
model.compile(optimizer='adam', loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(X_train, y_train, batch_size=64, epochs=10,
validation_data=(X_test, y_test))
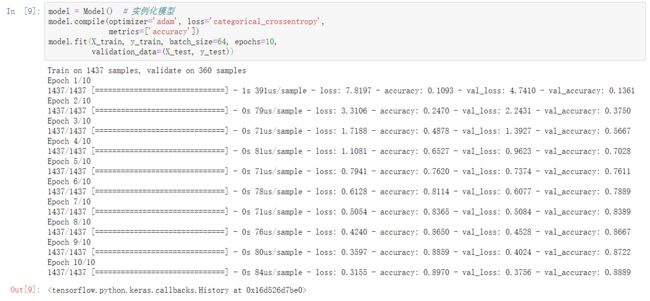
tf.keras.Model 模型
class Model(tf.keras.Model):
def __init__(self):
super(Model, self).__init__()
self.dense_1 = tf.keras.layers.Dense(30, activation='relu') # 初始化
self.dense_2 = tf.keras.layers.Dense(10, activation='softmax')
def call(self, inputs):
x = self.dense_1(inputs) # 前向传播过程
return self.dense_2(x)
model = Model() # 实例化模型
model.compile(optimizer='adam', loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(X_train, y_train, batch_size=64, epochs=10,
validation_data=(X_test, y_test))实验总结
本次实验中,我们实验中 TensorFlow 2.0 构建了简单的前馈神经网络,并完全手写字符识别分类。特别地,一定要掌握 Eager Execution 的实现过程,而对于 TensorFlow Keras 的使用也应用有充分的理解。