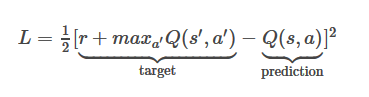最近在刷Mit的自动驾驶课程,里面的resources有很多很棒的材料,这里打算记个笔记,把一些概念整理一下,防止遗忘。
PART I
第一部分的一些概念主要翻译自这里
- Markov Decision Process (MDP)
- Discounted Future Reward
- Q-learning
- Deep Q Network
- Experience Replay
- Exploration-Exploitation
- Deep Q-learning Algorithm
Markov Decision Process
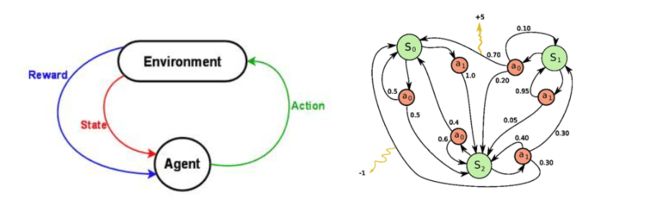
我们应该如何构建一个增强学习的问题呢?最常见的方法就是把需要解决的问题用马尔科夫决策过程(Markov Decision Process, MDP)来表示。
假设你是一个agent, 处在一个环境environment中(比如,atari breakout游戏), 这个环境又处于一个状态state中(state可以用paddle的位置,球的方向,每个砖块的位置等信息来表示)。agent在环境中可以做一些动作actions(比如,把paddle挪到左边或者右边)。这些action有的时候会让你得到一些奖励reward(比如,游戏得分增加了)。Actions会改变环境,变成到一个新的状态,然后agent又可以采取一个动作,以此类推。那么你如何选择这些动作被称之为policy。通常环境都是随机的,这意味这接下来的状态可能也是随机的(比如,你初始化游戏发球的时候,球的方向就是随机的)。
笔者注: 像象棋这种你下了一步棋之后的棋盘是确定不会变的,但是比如你复习期末考试的时候不认真复习出去溜达了一天,接下来你是否能通过考试就是不确定的。
这一系列的states,actions, 以及从一个状态转移到另一个状态的规则,合起来组成了一个MDP。这个过程的一个episode(比如,一局游戏)形成了一个有限的states, actions, rewards的序列:
这里si指的是state, ai指的是action, r_i+1是在状态si,采取了ai之后获得的奖励。这个episode以一个terminal state sn(比如,游戏结束)作为结束。一个MDP是基于马尔科夫假设的,下一个状态s_i+1只依赖于当前状态si和动作ai,而不和前面的状态以及动作有关。
Discounted Future Reward
为了在长远的角度上都表现好,我们不仅仅需要把即时得到的奖励算进去,还需要把未来的奖励算进去。那我们应该怎么算呢?
给定了一次MDP,我们可以很容易的计算出一个episode中的全部奖励total reward:
那么,对于某一个时刻t,这个时刻的未来的总奖励total future reward就可以表示为:
但是,因为我们的环境是随机不确定的,我们不能确保我们下次做相同的动作就一定可以得到相同的奖励。未来越是遥远,那么它就会更加的发散。因此,通常都会用discounted future reward(打折的未来奖励??):
这里的γ 是一个discounted factor折扣因子,在0-1之间,可以看到时间约长,未来的reward对当前的影响越小。而且在时刻t,discounted future reward就可以用t+1时刻的discounted future reward来表示:
如果令γ =0,那么我们的策略就是短视的,只看即时的奖励。如果我们想在即时的奖励和未来的奖励之间平衡,我们应该把折扣因子设置为像是γ =0.9这样子。如果我们的环境不是随机的,是确定的,那么相同的动作总是为导致相同的奖励,那么我们就可以令γ =1。
对于一个agent,一个好的策略通常是选择一个action来最大化将来的奖励(discounted future reward)。
Q-learning
在Q-learning中,我们定义一个函数Q(s,a)来表示当我们在状态s的时候,采取了行动a,会得到的最大的折扣的将来奖励:
可以这样来思考Q(s,a),实际上就是"在状态s的时候采取了行动a之后,我们在游戏结束后会得到的最好最有可能的分数"。这叫做Q-function,因为它表示的是在给定状态下,一个特定的行动action的“质量”(quality)。
也许会听起来是一个很困惑的定义。我们怎么能够在只知道当前状态和行动的情况下(而不是后面的那些行动和奖励),来评估游戏结束时候的得分呢?我们确实不行。但是,理论上我们可以假设有这么一个函数的存在。所以闭上眼睛,重复5遍,“Q(s, a) exists, Q(s, a) exists, …”. Feel it?
如果你还是不确定,就想一下有这样的一个函数意味着什么。假设你处在一个状态,在思考你是要采取行动a还是行动b。你想采取那个可以让你在游戏结束的时候得分最高的那个行动。一旦你有了神奇的Q-function,答案就非常简单啦 - 挑那个有最高Q-value的行动就好啦!
这里的π表示的是policy策略,就是我们在每个状态的时候该如何选择行动。
好的,那么我们应该怎么得到Q-function呢?我们就先考虑一个转移情况
这叫做Bellman equation。仔细想想是很合逻辑的--对于当前状态和行动的最大将来奖励就是即时奖励加上下个状态的最大将来奖励。
Q-learning的主要思想是我们可以用Bellman equation来迭代的来使其近似Q-function。
最简单的例子是把Q-function表示成一个表格,状态是行,行动是列。那么Q-learning算法表示如下:
随机初始化 Q[num_states, num_actions]
得到初始化状态s
repeat:
选择并且采取一个行动a
获得奖励r以及到达一个新状态s'
Q[s, a] = Q[s, a] + α(r + γ maxQ[s',a'] - Q[s,a])
s = s'
until terminated
α在算法中是learning rate学习率,控制的是在之前的Q-value和最新的Q-value之间的差异多少是要考虑进去的。 特别的是,当α=1,那么两个Q[s,a]就互相抵消,更新就和原来的Bellman equation一模一样了。
我们用来更新Q[s,a]的max_a’ Q[s’,a’]只是一个近似估计(approximation),在起初的学习阶段这个值也许完全就是不对的,然而,这个近似估计会随着每次的迭代越来越准确,这里有证明。只要我们更新的次数足够,Q-function就会收敛并且能够表示真正的Q-value。
Deep Q Network
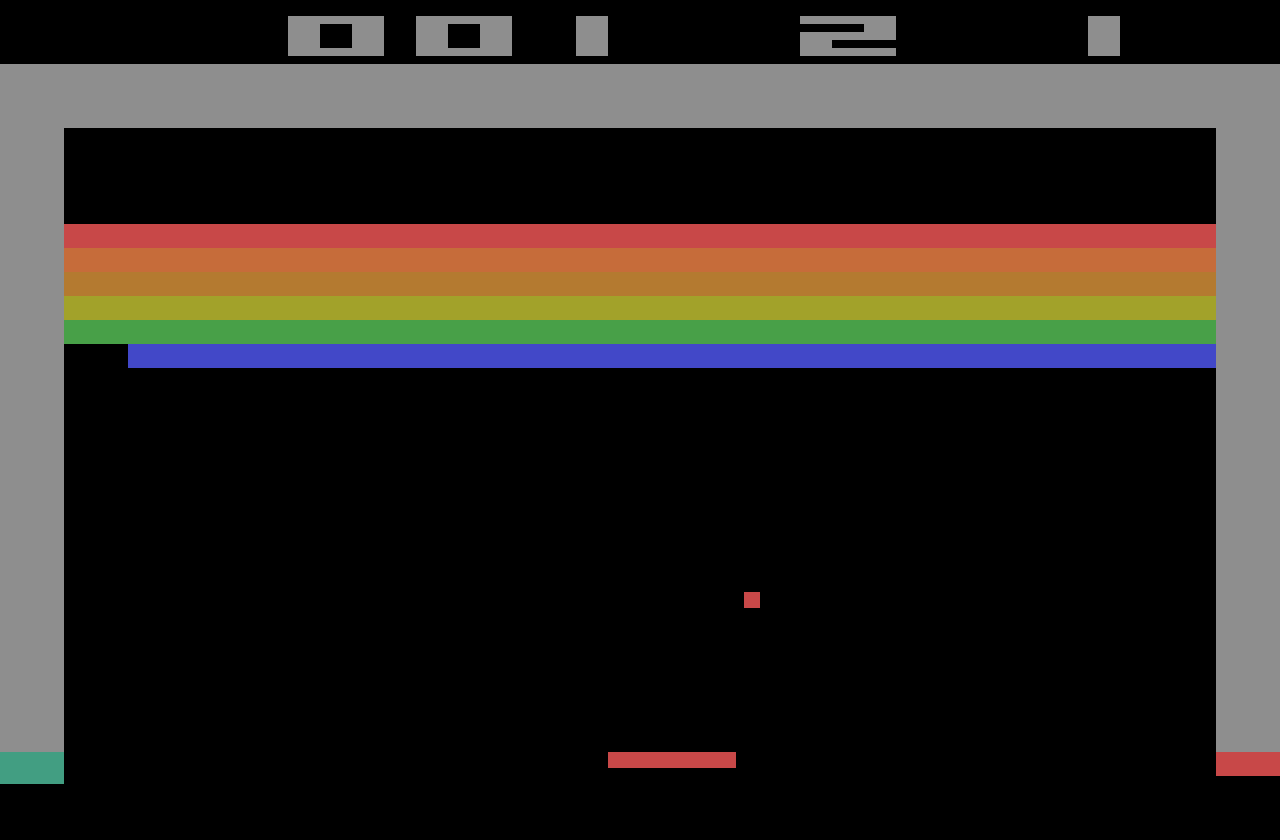
Breakout游戏(见下图)的环境状态state可以用paddle的位置,球的位置方向以及每个砖块是否存在来表示。然而这种直观的表示是跟特定的游戏相关的(换个游戏状态的表示就不一样了)。我们是不是可以用一种更通用的方法,可以适用于所有的游戏的方法呢?显然可以用屏幕的像素-它们隐含的包括了所有关于游戏状况的信息,除了球的方向和速度,两个连续的屏幕就可以把这些都包括了。
如果我们用和DeepMind论文中相同的游戏屏幕的预处理--用最近的四张屏幕图片,把他们resize成84x84,然后转换成灰度图(256个灰度值),我们就会有256^(84x84x4) ≈ 10^(67970)个可能的游戏状态。这就意味在我们虚拟的Q-table中需要有 10^(67970)行,这比已知宇宙中的原子总数还要多!也许会有人说一些像素的组合(状态)是不会出现的--我们也许可以把状态表示成稀疏表只存储访问过的状态。即使是这样,大多数的状态都很少被访问过,要让这个Q-table收敛也需要花费宇宙的整个lifetime!。
这也是用深度学习的意义。神经网络对于高度结构化数据非常擅长总结出好的特征。我们可以用一个神经网络来表示我们的Q-function,以状态(四个连续的游戏屏幕)和动作作为输入,然后输出相应的Q-value。或者我们可以只把游戏屏幕作为输入,为每个行动输出相应的Q-value。这个方法有这样的有点,如果我们想要更新一次Q-value或者选择有最高Q-value的那个行动,我们只用做一次前向,然后立即就得到所有行动的Q-value了。见下图:
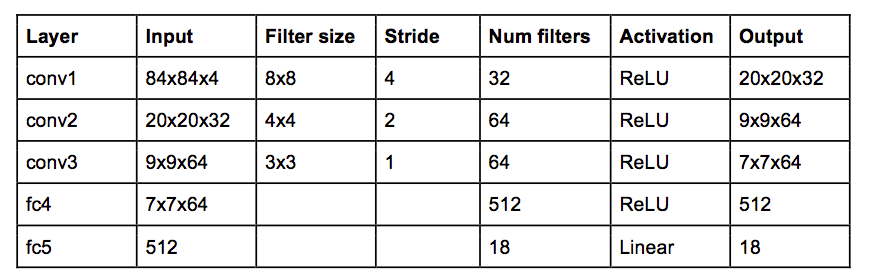
DeepMind用的网络架构如下:
这是一个经典的三层卷积层加两层全连接层的卷积神经网络。对物体识别网络熟悉的人也许会注意到没有pooling层。但是如果你仔细想一下,pooling层是为了不变性invariance--对于图片中物体的位置不敏感。对于ImageNet上面的分类任务来说是非常有意义的,但是对于游戏中球的位置是对于决定潜在的奖励是至关重要的,我们并不想抛弃这个信息。
网络的输入是4个84x84的灰度游戏屏幕。网络的输出是每个可能的行动(atari中是18)的Q-value值。Q-value可以是任意的实数值,就把这个问题变成了回归任务,用简单是平方差损失就可以来优化了:
给定了一次转移
- 对于当前状态s做一次前向,得到所有行动的Q-value值。
- 对下一个状态s'做一次前向,并且计算得到整个网络输出值的最大值max a’ Q(s’, a’).
- 对于当前动作的目标Q-value设置为 r + γmax a’ Q(s’, a’)(第2步里面计算得到的最大值)。对于其它动作,用1中得到的值设置他们的目标Q-value值,也就是说对于其它动作的error为0。
- 用反向传播更新权重。
Experience Replay
现在我们已经大概知道怎么用Q-learning以及用卷积网络来近似Q-function,从而可以在每个状态中估计将来奖励。但是用非线性函数来近似Q-value是非常不稳定的。要让它收敛需要一堆的tricks。而且在单块GPU上要花差不多一个星期的时间。
最重要的一个trick是experience replay。在游戏的时候,所有的经验
Exploration-Exploitation
Q-learning尝试去解决赋值问题-它适时传播奖励,直到它达到了关键的决策点,这也是所获得的奖励的实际原因。但是我们还没有接触exploration-exploitaion困境。
首先观察,当一个Q-table或者Q-network随机初始化,它的预测初始也是随机的。如果我们根据最高的Q-value选取一个行动,这个行动也因此是随机的,这个agent演示的也是最原始的"exploration"。随着Q-function收敛,它会返回更加一直的Q-values,exploration的总量也减少了。所以可以说,Q-learning把exploration融入了算法中,最为其中的一部分。但是这个exploration是"贪心"的,它用它找到的第一个有效的策略。
对上面问题的一个有效解决方法是 ε-greedy exploration,ε 的概率随机选择一个行动,否则就“贪心”的选择Q-value值最高的那个。在他们的系统中,DeepMind实际上随着时间逐渐减小ε,从1到0.1,期限系统是完全随机的去探索状态空间,接着就固定到一个固定的exploration rate。
Deep Q-learning Algorithm
这里给出最后的深度Q-learning算法+experience replay策略:
事实上DeepMind还做了很多tricks,像是target network, error clipping, reward clipping等等,但是这些对于这次的介绍还是超出了范围。
这个算法最让人惊讶的是,它学习到了东西。想一下,因为我们的Q-function是随机初始化的,所以它一开始输出的完全是垃圾。然后我们用这个垃圾(下一个状态的最大Q-value)最为网络的目标target,只是偶尔减少一点reward。这听起来很无脑,它怎么可能会学到有意义的东西呢?事实是,它就是学到了。
Final notes
自深度Q-learning第一次出现之后有了很多的改进 -- Double Q-learning, Prioritized Experience Replay, Dueling Network Architecture and extension to continuous action space 。最新的进展可以看 NIPS 2015 deep reinforcement learning workshop and ICLR 2016 (search for “reinforcement” in title). But beware, that deep Q-learning has been patented by Google. 但是注意,deep Q-learning已经被谷歌注册专利了。
我们总说人工智能是我们还没有搞明白的东西,一旦我们知道它是怎么运作的,它就不再看起来只能了。但是深度Q-networks仍然让我觉得惊讶。看它们知道怎么玩游戏就像是在野外观看动物 -- 它自给自足的经历(a rewarding experience by itself)。
Links
- David Silver’s lecture about deep reinforcement learning
- Slightly awkward but accessible illustration of Q-learning
- UC Berkley’s course on deep reinforcement learning
- David Silver’s reinforcement learning course
- Nando de Freitas’ course on machine learning (two lectures about reinforcement learning in the end)
- Andrej Karpathy’s course on convolutional neural networks
[1] Algorithm adapted from http://artint.info/html/ArtInt_265.html