manifold
可以称之为流形数据。像绳结一样的数据,虽然在高维空间中可分,但是在人眼所看到的低维空间中,绳结中的绳子是互相重叠的不可分的。
t-SNE
t-SNE是目前来说效果最好的数据降维与可视化方法,但是它的缺点也很明显,比如:占内存大,运行时间长。但是,当我们想要对高维数据进行分类,又不清楚这个数据集有没有很好的可分性(即同类之间间隔小,异类之间间隔大),可以通过t-SNE投影到2维或者3维的空间中观察一下。如果在低维空间中具有可分性,则数据是可分的。如果在低维空间中不具有可分性,可能是数据不可分,也可能仅仅是因为不能投影到低维空间。
t-SNE将数据点之间的相似度转换为概率。原始空间中的相似度由高斯联合概率表示,嵌入空间的相似度由“学生t分布”表示。
通过原始空间和嵌入空间的联合概率的Kullback-Leibler(KL)散度来评估可视化效果的好坏,也就是说用有关KL散度的函数作为loss函数,然后通过梯度下降最小化loss函数,最终获得收敛结果。需要注意的是该loss函数不是凸函数,即具有不同初始值的多次运行可能收敛到KL散度函数的不同局部最小值,获得不同的结果。因此可以尝试不同的随机数种子(Python中可以通过设置seed来获得不同的随机分布),最后选择具有最低KL散度值的结果。
t-SNE的缺点是:
- t-SNE的计算复杂度很高,在数百万个样本数据集中可能需要几个小时,而PCA可以在几秒钟或几分钟内完成。
- Barnes-Hut t-SNE方法(下面讲)限于二维或三维嵌入。
- 算法是随机的,具有不同种子的多次实验可以产生不同的结果。虽然选择loss最小的结果就行,但可能需要多次实验以选择超参数。
- 全局结构未明确保留。这个问题可以通过PCA初始化点(使用init ='pca')来缓解。
t-SNE的主要目的是高维数据的可视化。因此,当数据嵌入二维或三维时,效果最好。有五个参数可以控制t-SNE的优化,即会影响最后的可视化质量:
- perplexity:困惑度
- early exaggeration factor:前期放大系数
- learning rate:学习率
- maximum number of iterations:最大迭代次数
- angle: 角度
Barnes-Hut t-SNE
Barnes-Hut t-SNE主要是对传统t-SNE在速度上做了优化,是现在最流行的t-SNE方法,同时它与传统t-SNE还有一些不同:
- Barnes-Hut仅在目标维度为3或更小时才起作用。以2D可视化为主。
- Barnes-Hut仅适用于密集的输入数据。稀疏数据矩阵只能用特定的方法嵌入,或者可以通过投影近似,例如使用sklearn.decomposition.TruncatedSVD
- Barnes-Hut是一个近似值。使用angle参数对近似进行控制,当参数
method="exact"时,TSNE()使用传统方法,此时angle参数不能使用。 - Barnes-Hut可以处理更多的数据。 Barnes-Hut可用于嵌入数十万个数据点。
为了可视化的目的(这是t-SNE的主要用处),强烈建议使用Barnes-Hut方法。method="exact"时,传统的t-SNE方法尽管可以达到该算法的理论极限,效果更好,但受制于计算约束,只能对小数据集的可视化。
注意事项
数据集在所有特征维度上的尺度应该相同。
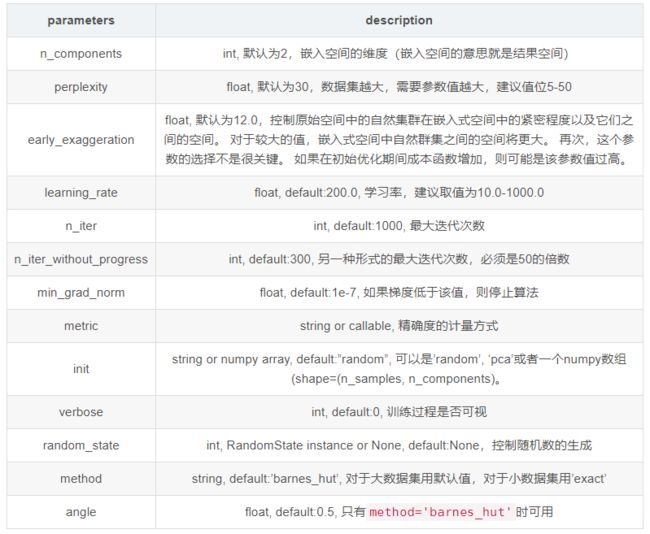
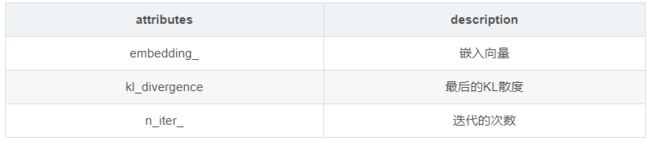
参数说明
例子
import numpy as np
from time import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import NullFormatter
from sklearn import manifold, datasets
%matplotlib inline
X = np.array([[0, 0, 0], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
tsne = manifold.TSNE(n_components=2)
tsne.fit_transform(X)
print(tsne.embedding_)
// 输出
[[-520.725 302.84378 ]
[-116.2318 369.94275 ]
[-453.6018 -101.645386]
[ -49.10863 -34.546448]]
n_points = 1000
X, color = datasets.samples_generator.make_s_curve(n_points, random_state=0)
n_neighbors = 10
n_components = 2
print(X.shape)
print(X[:10])
print(color.shape)
print(color[:10])
// 输出
(1000, 3)
[[ 0.44399868 1.18576054 -0.10397256]
[ 0.89724097 0.02012739 -1.44154121]
[ 0.8240493 0.95165239 -0.43348191]
[ 0.41051068 1.41754078 -0.08814421]
[-0.65903619 0.08795086 0.24788877]
[ 0.98089687 1.75904297 -0.80547154]
[-0.55488662 1.04016283 0.16807402]
[-0.5233528 0.0613221 -1.8521161 ]
[-0.94192794 0.44882722 -1.33581507]
[-0.89054316 1.90735139 0.54510124]]
(1000,)
[ 0.46005644 2.028112 0.968522 0.42301403 -0.71953656 1.37501962
-0.58822668 3.69237354 4.36991857 -1.0985378 ]
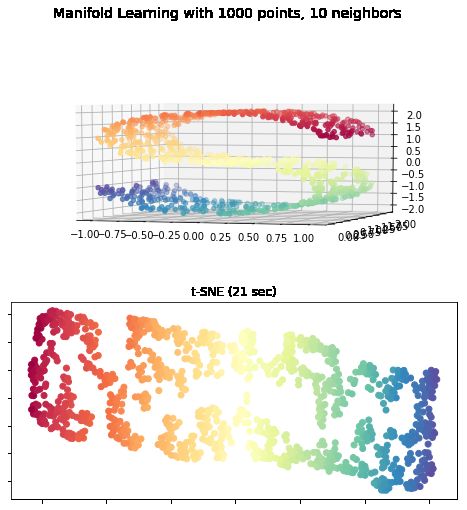
fig = plt.figure(figsize=(8, 8))
# 创建了一个figure,标题为"Manifold Learning with 1000 points, 10 neighbors"
plt.suptitle("Manifold Learning with %i points, %i neighbors"
% (1000, n_neighbors), fontsize=14)
'''绘制S曲线的3D图像'''
ax = fig.add_subplot(211, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)
ax.view_init(4, -72) # 初始化视角
# t=SME
t0 = time()
tsne = manifold.TSNE(n_components=n_components, init='pca', random_state=0)
Y = tsne.fit_transform(X) # 转换后的输出
t1 = time()
print("t-SNE: %.2g sec" % (t1 - t0)) # 打印算法用时
ax = fig.add_subplot(2, 1, 2)
plt.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral)
plt.title("t-SNE (%.2g sec)" % (t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter()) # 设置标签显示格式为空
ax.yaxis.set_major_formatter(NullFormatter())
plt.show()
// 输出
t-SNE: 21 sec
参考
数据降维与可视化——t-SNE