引言:
邢不行的系列帖子“量化小讲堂”,通过实际案例教初学者使用python进行量化投资,了解行业研究方向,希望能对大家有帮助。
【历史文章汇总】请点击此处
【必读文章】EOS期现套利,一周时间,15%无风险收益
10年400倍策略分享(附视频逐行代码讲解)
个人微信:xingbuxing0807,有问题欢迎交流。
文中用到的A股数据可在www.yucezhe.com下载,这里可以下载到所有股票、从上市日起的交易数据、财务数据、分钟数据、分笔数据、逐笔数据等。
诺奖得主的仓位分配算法,有效吗?
假设你有1千万准备投资股票,你从A股接近3000只股票当中挑选出了50只,准备把这50只股票作为一个投资组合打包购买。那么在这50只股票之间应该如何分配仓位才是最好的呢?是平均每个股票各买20万,还是有的股票多买点有的股票少买点?
如何在这些股票之间分配仓位?这个问题就是诺贝尔奖得主马克维茨(Harry Markowitz)在1952年通过数学方法解决的问题。他也为此而拿到了诺贝尔奖。
马克维茨提出的解决方案叫做资产组合理论。感兴趣的可以看看附件中的论文原文,也可以看又一斋主的这篇文章《马克维茨与投资组合理论》。
本文的主要目是和大家分享如何使用Python在A股市场实证资产组合理论。所以在这里简单的讲一下理论的具体原理。会尽量写的浅显,目标是让高中生也可以看懂。建议感兴趣的同学可以先看本篇文章,大概了解后再去阅读又一斋主的文章。
资产组合理论
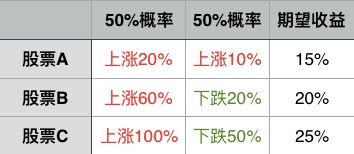
假设现在有3只股票A、B、C。股票A,在一年后有一半概率上涨20%,一半的概率上涨10%。它的期望收益是15%(计算方法:20% * 0.5 + 10% * 0.5);股票B在一年后有一半概率上涨60%,一半概率下跌20%,期望收益20%;股票C有一半概率上涨100%,一半概率下跌50%,期望收益25%。具体如下:
在这三个股票中选择一个股票进行买卖,你会选择哪个呢?我觉得选择任何股票都是正常的。选择股票A的人比较保守,虽然赚的少一点,但是毕竟任何情况下都是稳赚(风险小)。选择股票B的话,差的情况下也就亏20%,好得情况下可以赚60%,相当高的收益了。选择股票C的人其实也能理解,毕竟富贵险中求(风险大),虽然可能亏一半,但是翻倍的诱惑还是巨大的。汝之蜜糖彼之砒霜,适合自己的才是最好的。
在从这3个股票当中进行选择的时候,你有没有发现其实你是在权衡每个股票的收益和风险。我们往往希望收益越高越好,风险越低越好。然而金融领域自打有宇宙以来的第一定律就是高收益和低风险不可兼得。收益高,往往风险也高,风险低往往收益也就低了。人生又何尝不是如此呢?所以我们只能根据自己的偏好在收益和风险之间进行权衡。那用什么方式来定量化的刻画股票的风险呢?——用方差。
对,就是初中课堂上学习过的方差。方差用来描述一组数据之间的离散程度,而收益的离散程度就是风险。比如对于股票A,它的方差就是[(0.2 - 0.15)^2 + (0.1 - 0.15)^2] / 2 = 0.0025。同理,股票B和股票C的方差分别是0.16和0.5625。股票的风险越大,它的方差也就越大,反之,方差大说明这个股票的风险也大。
了解了方差之后,我们回到从3个股票当中选择一个进行投资的话题上来。我估计大多数人会选择B股票,冒着亏不多钱的风险,赚取60%的收益。
这时候有的聪明人就会说,我能不能这样来投资:我将所有的钱平均分成两份,一份全部买股票A,一份全部买C形成一个组合,这个组合里面有A、C两只股票,那么这整个组合一年后的期望收益是20%,跟股票B是一样的,而我一年后收益的可能性是:
- 25%的概率上涨60%(A涨20%,C涨100%)
- 25%的概率上涨55%(A涨10%,C涨100%)
- 25%的概率下跌15%(A涨20%,C跌50%)
- 25%的概率上涨20%(A涨10%,C跌50%)
收益的方差是0.14125,比股票B的方差0.16小。也就是说我通过构建了一个组合,得到了一个和B期望收益一样,但是风险比B小的投资。相比于这个投资组合,全仓买股票B显然就是一个很蠢的选择。
更聪明的人这个时候又要问了:刚刚是在A、C两只股票里面平均分配50%的仓位购进组合,那么是不是存在另外的一种分配方式,使得这个组合在20%的期望收益下,风险(方差)可以更小呢?或者说我想要的期望收益是25%,怎么在3只股票里面分配仓位,保证组合方差最小呢?或者说我想要0.1的方差,怎么在3只股票里面分配仓位,保证我组合的期望收益最大呢?(感兴趣的话真的可以动笔算算,很有意思。)
其实以上这些就是马克维茨想要解决的问题:怎么才能在一堆股票当中通过分配仓位,来使整个组合的期望收益尽可能的高,风险(方差)尽可能的低。或者说,在一定的期望收益下,风险尽可能的低;在一定的风险条件下,期望收益尽可能的高。
这时候你可能会讲:这看上去也没什么难度嘛,就算是离诺奖无穷远的我,即使多花点时间也能算出最优的仓位呀。是的,以上的计算确实并不复杂。因为,因为,因为——
因为我们在计算当中想当然的多增加了一个条件:我们假设这些股票之间的收益是相互独立的。也就是股票和股票之间的收益不会相互影响。
然而现实中所有股票之间的收益都是相关的啊!!!
工商银行上涨的时候,农业银行大概率也会上涨吧?京东股票涨得时候,阿里的股票有可能会跌吧?2015年7月份千股跌停、千股涨停等现象,这些都是在说明股票之间会有相关性。所以上面A、B、C三只股票的问题,可能会变成股票A上涨的时候,股票B也有80%的概率上涨;股票A上涨的时候,股票C却有60%的概率下跌......这个时候想要算出个最优仓位比例,就比较麻烦了吧?
而人家马克维茨牛逼就牛逼在,即使考虑到股票之间的相关性,他也找到了计算的方法。
他使用相关系数来衡量股票之间的相关性。相关系数的取值范围是-1到1,越接近1代表这两个股票的收益越正相关(工行和农行),越接近-1代表这两个股票的收益越负相关(阿里和京东),接近0则代表不相关。他假设已知N个股票未来一段时间的期望收益、收益的方差,以及这些股票两两之间之间的相关系数,仅仅知道这些,就可以计算出最优的仓位比例,来保证我们的投资组合获得尽可能高的收益以及相应尽可能低的风险。
人家具体怎么算的我就不细说了,是个纯数学问题,归根到底是一个标准的凸二次规划问题。具体可以看论文原文或者又一斋主的文章。本文重点关注的是如何将马克维茨的理论真正的投入到实战中去。
实战
要把马克维茨的方案运用到投资实战中,最大的难点就是要确定模型的输入参数。必须得知道这些股票的期望收益、方差以及两两间的相关系数才能计算最终的仓位啊,可是到底怎么才能知道股票未来一年的期望收益、方差、以及相关系数呢?(这几乎不可能嘛)
实战中一般的做法就是拿股票过去一段时间的收益来估计这些参数。落实到具体的策略,我们是采用如下方法来构建的:在每月的最后一个交易日收盘后,根据过去6个月(这个数字可以自己设定)的历史数据计算出每个备选股票的收益、方差、相关系数,将这些数据作为参数,套入到马克维茨的方法中,计算出每个股票的最优仓位。按计算出来的仓位买入这些股票并持有整个下个月,在下月末再按照该方法,根据最新的过去6个月的数据重新计算仓位,进行调整,再持有一个月,如此往复。
其中,在采用马克维茨的方法计算最优仓位的时候,我们的优化目标是最优夏普比例,也就是最大化期望收益/方差。在程序中也可以调整为最优收益或者最优方差。
为了方便起见,我们以沪深300指数,中小板指数,还有创业板指数为例,假设我们是要投资这3个指数,并在这3个指数之间分配仓位。当然在程序中你也可以自己通过修改代码来尝试在更多的股票、指数之间进行分配仓位。
程序
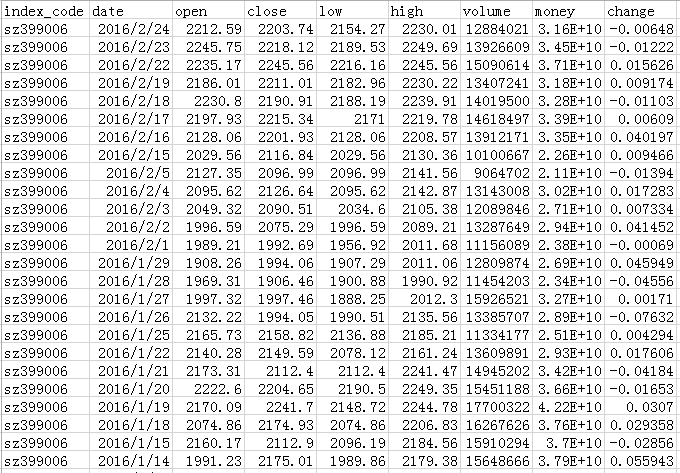
要用三大指数构造投资组合,首先需要指数的原始数据。在yucezhe.com的历史日线数据中,可以下载到所有指数历史至今的数据。如下图所示,每一行是每一天的数据:
数据中有以下的字段:
【index_code】指数的代码
【date】 交易日期
【open】 开盘价
【high】 最高价
【low】 最低价
【close】 收盘价
【volume】 成交量
【money】 成交额
【change】 涨跌幅
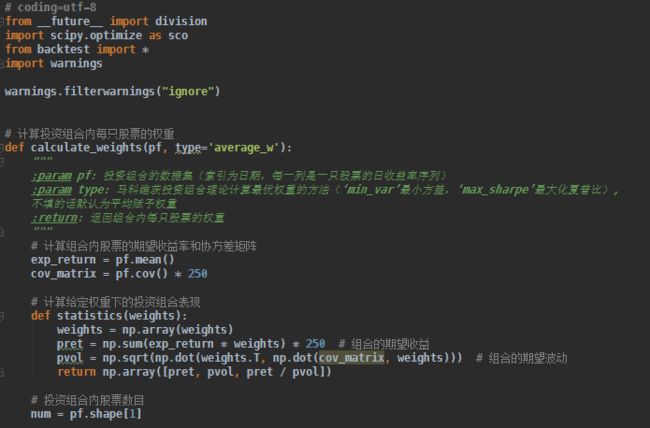
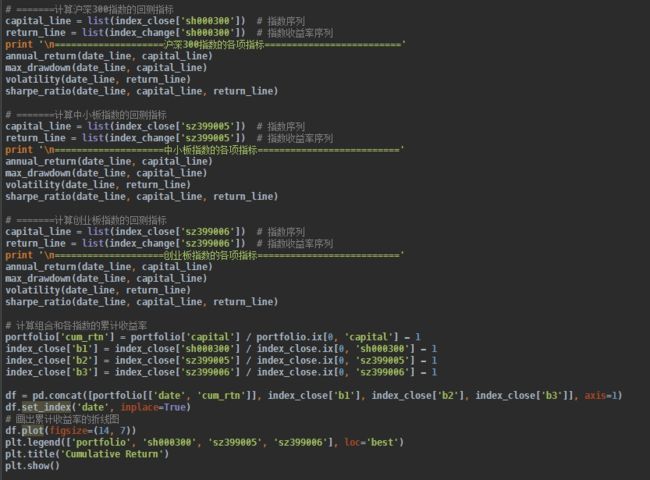
下面是代码的截图,代码里面有详细的注释,有问题可以留言,附件中有程序的源码,回复即可下载。
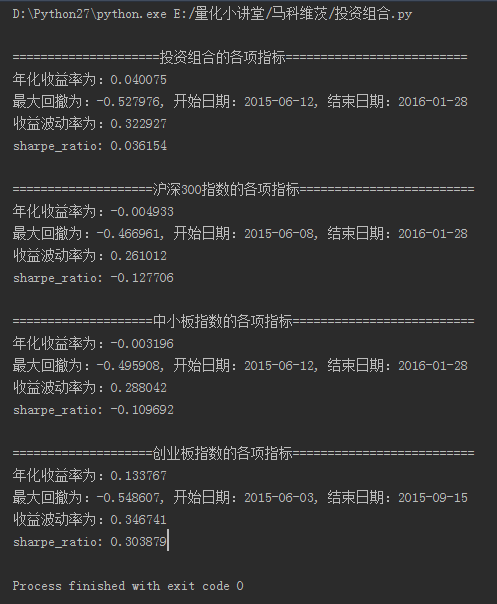
把代码和数据下载下来,运行代码,就可以看到输出的结果了。
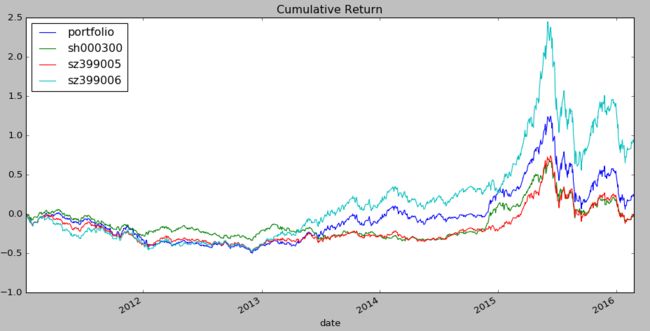
数据的回测是从2011年开始的(因为创业板指数开始时间较晚)。从结果中可以看到,通过马克维茨的方法构建的投资组合的年化收益率是高于沪深300、中小板指数,但低于创业板指数。在风险方面,由于是采用的最大化夏普比的方法,所以最大回撤还是略大于沪深300和中小板的。
大家下载程序后,可以把3个指数改成其他的股票,尝试着在不同的股票之间进行仓位的配置,看看效果。
此处也留一个思考题:是否能搞到余额宝的每日收益率,作为无风险利率,也作为组合中的一个备选资产。这样就能算出投资股票和投资余额宝的仓位比例的。
对本文研究有自己的想法的朋友,欢迎在评论区留言。关于文中的代码、数据,以及下期《量化小讲堂》想了解的内容,也可以加我个人微信xingbuxing0807交流。
如果你想入门量化,但是始终找不到方向,可以加入我的知识星球。我会在里面解答你的问题,分享我的感悟,不论是投资、技术,还是职业选择、思维方式。
-- 学习和成长从来都不是一个人的事 --