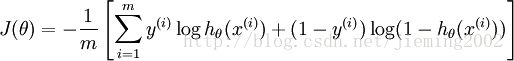参考资料(要是对于本文的理解不够透彻,必须将以下博客认知阅读,方可全面了解LR):
(1).https://zhuanlan.zhihu.com/p/74874291
(2).逻辑回归与交叉熵
(3).https://www.cnblogs.com/pinard/p/6029432.html
(4).https://zhuanlan.zhihu.com/p/76563562
(5).https://www.cnblogs.com/ModifyRong/p/7739955.html
(6).生成模型和判别模型的区别
一、逻辑回归介绍
逻辑回归(Logistic Regression)是一种广义线性回归。线性回归解决的是回归问题,预测值是实数范围,逻辑回归则相反,解决的是分类问题,预测值是[0,1]范围。所以逻辑回归名为回归,实为分类。接下来让我们用一句话来概括逻辑回归(LR):
逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的。
这句话包含了五点,接下来一一介绍:
- 逻辑回归的假设
- 逻辑回归的损失函数
- 逻辑回归的求解方法
- 逻辑回归的目的
- 逻辑回归如何分类
二、逻辑回归的假设
任何的模型都是有自己的假设,在这个假设下模型才是适用的。逻辑回归的第一个基本假设是假设数据服从伯努利分布。
伯努利分布:是一个离散型概率分布,若成功,则随机变量取值1;若失败,随机变量取值为0。成功概率记为p,失败为q = 1-p。
在逻辑回归中,既然假设了数据分布服从伯努利分布,那就存在一个成功和失败,对应二分类问题就是正类和负类,那么就应该有一个样本为正类的概率p,和样本为负类的概率q = 1- p。具体我们写成这样的形式:
逻辑回归的第二个假设是正类的概率由sigmoid的函数计算,即:
即:
写在一起:
个人理解,解释一下这个公式,并不是用了样本的标签y,而是说你想要得到哪个的概率,y = 1时意思就是你想得到正类的概率,y = 0时就意思是你想要得到负类的概率。另外在求参数时,这个y是有用的,这点在下面会说到。
另外关于这个值, 是个概率,还没有到它真正能成为预测标签的地步,更具体的过程应该是分别求出正类的概率,即y = 1时,和负类的概率,y = 0时,比较哪个大,因为两个加起来是1,所以我们通常默认的是只用求正类概率,只要大于0.5即可归为正类,但这个0.5是人为规定的,如果愿意的话,可以规定为大于0.6才是正类,这样的话就算求出来正类概率是0.55,那也不能预测为正类,应该预测为负类。
理解了二元分类回归的模型,接着我们就要看模型的损失函数了,我们的目标是极小化损失函数来得到对应的模型系数θ。
三、逻辑回归的损失函数
回顾下线性回归的损失函数,由于线性回归是连续的,所以可以使用模型误差的的平方和来定义损失函数。但是逻辑回归不是连续的,自然线性回归损失函数定义的经验就用不上了。不过我们可以用最大似然法(MLE)来推导出我们的损失函数。有点人把LR的loss function成为log损失函数,也有人把它称为交叉熵损失函数(Cross Entropy)。
如何理解这句话呢?
再联系到逻辑回归里,一步步来分解上面这句话,首先确定一下模型是否已定,模型就是用来预测的那个公式:
参数就是里面的 ,那什么是样本结果信息,就是我们的x,y,是我们的样本,分别为特征和标签,我们的已知信息就是在特征取这些值的情况下,它应该属于y类(正或负)。
反推最具有可能(最大概率)导致这些样本结果出现的参数,举个例子,我们已经知道了一个样本点,是正类,那么我们把它丢入这个模型后,它预测的结果一定得是正类啊,正类才是正确的,才是我们所期望的,我们要尽可能的让它最大,这样才符合我们的真实标签。反过来一样的,如果你丢的是负类,那这个式子计算的就是负类的概率,同样我们要让它最大,所以此时不用区分正负类。
这样串下来,一切都说通了,概括一下:
一个样本,不分正负类,丢入模型,多的不说,就是一个字,让它大
一直只提了一个样本,但对于整个训练集,我们当然是期望所有样本的概率都达到最大,也就是我们的目标函数,本身是个联合概率,但是假设每个样本独立,那所有样本的概率就可以由以下公式推到:
设:
似然函数:
为了更方便求解,我们对等式两边同取对数,写成对数似然函数:
在机器学习中我们有损失函数的概念,其衡量的是模型预测错误的程度。如果取整个数据集上的平均对数似然损失,我们可以得到:
即在逻辑回归模型中,我们最大化似然函数和最小化损失函数实际上是等价的。所以说LR的loss function可以由MLE推导出来。
四、逻辑回归损失函数的求解
解逻辑回归的方法有非常多,主要有梯度下降(一阶方法)和牛顿法(二阶方法)。优化的主要目标是找到一个方向,参数朝这个方向移动之后使得损失函数的值能够减小,这个方向往往由一阶偏导或者二阶偏导各种组合求得。逻辑回归的损失函数是:
随机梯度下降:梯度下降是通过 J(w) 对 w 的一阶导数来找下降方向,初始化参数w之后,并且以迭代的方式来更新参数,更新方式为 :
其中 k 为迭代次数。每次更新参数后,可以通过比较 小于阈值或者到达最大迭代次数来停止迭代。
梯度下降又有随机梯度下降,批梯度下降,small batch 梯度下降三种方式:
- 简单来说 批梯度下降会获得全局最优解,缺点是在更新每个参数的时候需要遍历所有的数据,计算量会很大,并且会有很多的冗余计算,导致的结果是当数据量大的时候,每个参数的更新都会很慢。
- 随机梯度下降是以高方差频繁更新,优点是使得sgd会跳到新的和潜在更好的局部最优解,缺点是使得收敛到局部最优解的过程更加的复杂。
- 小批量梯度下降结合了sgd和batch gd的优点,每次更新的时候使用n个样本。减少了参数更新的次数,可以达到更加稳定收敛结果,一般在深度学习当中我们采用这种方法。
加分项,看你了不了解诸如Adam,动量法等优化方法(在这就不展开了,以后有时间的话专门写一篇关于优化方法的)。因为上述方法其实还有两个致命的问题:
- 第一个是如何对模型选择合适的学习率。自始至终保持同样的学习率其实不太合适。因为一开始参数刚刚开始学习的时候,此时的参数和最优解隔的比较远,需要保持一个较大的学习率尽快逼近最优解。但是学习到后面的时候,参数和最优解已经隔的比较近了,你还保持最初的学习率,容易越过最优点,在最优点附近来回振荡,通俗一点说,就很容易学过头了,跑偏了。
- 第二个是如何对参数选择合适的学习率。在实践中,对每个参数都保持的同样的学习率也是很不合理的。有些参数更新频繁,那么学习率可以适当小一点。有些参数更新缓慢,那么学习率就应该大一点。
有关梯度下降原理以及优化算法详情见我的博客:
3种类型的梯度下降算法总结
李宏毅机器学习笔记2:Gradient Descent(附带详细的原理推导过程)
任何模型都会面临过拟合问题,所以我们也要对逻辑回归模型进行正则化考虑。常见的有L1正则化和L2正则化。
L1 正则化
LASSO 回归,相当于为模型添加了这样一个先验知识:w 服从零均值拉普拉斯分布。 首先看看拉普拉斯分布长什么样子:
由于引入了先验知识,所以似然函数这样写:
取 log 再取负,得到目标函数:
等价于原始损失函数的后面加上了 L1 正则,因此 L1 正则的本质其实是为模型增加了“模型参数服从零均值拉普拉斯分布”这一先验知识。
L2 正则化
Ridge 回归,相当于为模型添加了这样一个先验知识:w 服从零均值正态分布。
首先看看正态分布长什么样子:
由于引入了先验知识,所以似然函数这样写:
取 ln 再取负,得到目标函数:
等价于原始的损失函数后面加上了 L2 正则,因此 L2 正则的本质其实是为模型增加了“模型参数服从零均值正态分布”这一先验知识。
其余有关正则化的内容详见:L0、L1、L2范数正则化
五、逻辑回归的目的
该函数的目的便是将数据二分类,提高准确率。
六、逻辑回归如何分类
这个在上面的时候提到了,要设定一个阈值,判断正类概率是否大于该阈值,一般阈值是0.5,所以只用判断正类概率是否大于0.5即可。
七、为什么LR不使用平方误差(MSE)当作损失函数?
1. 平方误差损失函数加上sigmoid的函数将会是一个非凸的函数,不易求解,会得到局部解,用对数似然函数得到高阶连续可导凸函数,可以得到最优解。
2. 其次,是因为对数损失函数更新起来很快,因为只和x,y有关,和sigmoid本身的梯度无关。如果你使用平方损失函数,你会发现梯度更新的速度和sigmod函数本身的梯度是很相关的。sigmod函数在它在定义域内的梯度都不大于0.25。这样训练会非常的慢。
八、逻辑回归的优缺点
优点:
- 形式简单,模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响,某个特征的权重值比较高,那么这个特征最后对结果的影响会比较大。
- 模型效果不错。在工程上是可以接受的(作为baseline),如果特征工程做的好,效果不会太差,并且特征工程可以大家并行开发,大大加快开发的速度。
- 训练速度较快。分类的时候,计算量仅仅只和特征的数目相关。并且逻辑回归的分布式优化sgd发展比较成熟,训练的速度可以通过堆机器进一步提高,这样我们可以在短时间内迭代好几个版本的模型。
- 资源占用小,尤其是内存。因为只需要存储各个维度的特征值。
- 方便输出结果调整。逻辑回归可以很方便的得到最后的分类结果,因为输出的是每个样本的概率分数,我们可以很容易的对这些概率分数进行cut off,也就是划分阈值(大于某个阈值的是一类,小于某个阈值的是一类)。
缺点:
- 准确率并不是很高。因为形式非常的简单(非常类似线性模型),很难去拟合数据的真实分布。
- 很难处理数据不平衡的问题。举个例子:如果我们对于一个正负样本非常不平衡的问题比如正负样本比 10000:1.我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器,它对正负样本的区分能力不会很好。
- 处理非线性数据较麻烦。逻辑回归在不引入其他方法的情况下,只能处理线性可分的数据,或者进一步说,处理二分类的问题 。
- 逻辑回归本身无法筛选特征。有时候,我们会用gbdt来筛选特征,然后再上逻辑回归。
西瓜书中提到了如何解决LR缺点中的蓝色字体所示的缺点:
九、 逻辑斯特回归为什么要对特征进行离散化。
- 非线性!非线性!非线性!逻辑回归属于广义线性模型,表达能力受限;单变量离散化为N个后,每个变量有单独的权重,相当于为模型引入了非线性,能够提升模型表达能力,加大拟合; 离散特征的增加和减少都很容易,易于模型的快速迭代;
- 速度快!速度快!速度快!稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展;
- 鲁棒性!鲁棒性!鲁棒性!离散化后的特征对异常数据有很强的鲁棒性:比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰;
- 方便交叉与特征组合:离散化后可以进行特征交叉,由M+N个变量变为M*N个变量,进一步引入非线性,提升表达能力;
- 稳定性:特征离散化后,模型会更稳定,比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是门学问;
- 简化模型:特征离散化以后,起到了简化了逻辑回归模型的作用,降低了模型过拟合的风险。
十、与其他模型的对比
与SVM
相同点
1. 都是线性分类器。本质上都是求一个最佳分类超平面。都是监督学习算法。
2. 都是判别模型。通过决策函数,判别输入特征之间的差别来进行分类。
- 常见的判别模型有:KNN、SVM、LR。
- 常见的生成模型有:朴素贝叶斯,隐马尔可夫模型。
不同点
- 逻辑回归基于概率理论,假设样本为正样本的概率可以用sigmoid函数(S型函数)来表示,然后通过极大似然估计的方法估计出参数的值。
- 支持向量机基于几何间隔最大化原理,认为存在最大几何间隔的分类面为最优分类面。
(2). 两个模型对数据和参数的敏感程度不同
- SVM考虑分类边界线附近的样本(决定分类超平面的样本)。在支持向量外添加或减少任何样本点对分类决策面没有任何影响;
- LR受所有数据点的影响。直接依赖数据分布,每个样本点都会影响决策面的结果。如果训练数据不同类别严重不平衡,则一般需要先对数据做平衡处理,让不同类别的样本尽量平衡。
- LR 是参数模型,SVM 是非参数模型,参数模型的前提是假设数据服从某一分布,该分布由一些参数确定(比如正太分布由均值和方差确定),在此基础上构建的模型称为参数模型;非参数模型对于总体的分布不做任何假设,只是知道总体是一个随机变量,其分布是存在的(分布中也可能存在参数),但是无法知道其分布的形式,更不知道分布的相关参数,只有在给定一些样本的条件下,能够依据非参数统计的方法进行推断。
(3). SVM 基于距离分类,LR 基于概率分类。
- SVM依赖数据表达的距离测度,所以需要对数据先做 normalization;LR不受其影响。
(4). 在解决非线性问题时,支持向量机采用核函数的机制,而LR通常不采用核函数的方法。
- SVM算法里,只有少数几个代表支持向量的样本参与分类决策计算,也就是只有少数几个样本需要参与核函数的计算。
- LR算法里,每个样本点都必须参与分类决策的计算过程,也就是说,假设我们在LR里也运用核函数的原理,那么每个样本点都必须参与核计算,这带来的计算复杂度是相当高的。尤其是数据量很大时,我们无法承受。所以,在具体应用时,LR很少运用核函数机制。
(5). 在小规模数据集上,Linear SVM要略好于LR,但差别也不是特别大,而且Linear SVM的计算复杂度受数据量限制,对海量数据LR使用更加广泛。
(6). SVM的损失函数就自带正则,而 LR 必须另外在损失函数之外添加正则项。

那怎么根据特征数量和样本量来选择SVM和LR模型呢?Andrew NG的课程中给出了以下建议:
- 如果Feature的数量很大,跟样本数量差不多,这时候选用LR或者是Linear Kernel的SVM
- 如果Feature的数量比较小,样本数量一般,不算大也不算小,选用SVM+Gaussian Kernel
- 如果Feature的数量比较小,而样本数量很多,需要手工添加一些feature变成第一种情况。(LR和不带核函数的SVM比较类似。)
插入一个知识点:判别模型与生成模型的区别?
公式上看
- 生成模型: 学习时先得到P(x,y),继而得到 P(y|x)。预测时应用最大后验概率法(MAP)得到预测类别 y。
- 判别模型: 直接学习得到P(y|x),利用MAP得到 y。或者直接学得一个映射函数 y=f(x) 。
直观上看
- 生成模型: 关注数据是如何生成的
- 判别模型: 关注类别之间的差别
数据要求:生成模型需要的数据量比较大,能够较好地估计概率密度;而判别模型对数据样本量的要求没有那么多。
更多区别见生成模型和判别模型的区别
与朴素贝叶斯
相同点
朴素贝叶斯和逻辑回归都属于分类模型,当朴素贝叶斯的条件概率 服从高斯分布时,它计算出来的 P(Y=1|X) 形式跟逻辑回归是一样的。
不同点
- 逻辑回归是判别式模型 p(y|x),朴素贝叶斯是生成式模型 p(x,y):判别式模型估计的是条件概率分布,给定观测变量 x 和目标变量 y 的条件模型,由数据直接学习决策函数 y=f(x) 或者条件概率分布 P(y|x) 作为预测的模型。判别方法关心的是对于给定的输入 x,应该预测什么样的输出 y;而生成式模型估计的是联合概率分布,基本思想是首先建立样本的联合概率概率密度模型 P(x,y),然后再得到后验概率 P(y|x),再利用它进行分类,生成式更关心的是对于给定输入 x 和输出 y 的生成关系;
- 朴素贝叶斯的前提是条件独立,每个特征权重独立,所以如果数据不符合这个情况,朴素贝叶斯的分类表现就没逻辑会好了。
十一、多分类问题(LR解决多分类问题)
参考西瓜书!!!
现实中我们经常遇到不只两个类别的分类问题,即多分类问题,在这种情形下,我们常常运用“拆分”的策略,通过多个二分类学习器来解决多分类问题,即将多分类问题拆解为多个二分类问题,训练出多个二分类学习器,最后将多个分类结果进行集成得出结论。最为经典的拆分策略有三种:“一对一”(OvO)、“一对其余”(OvR)和“多对多”(MvM),核心思想与示意图如下所示。
-
OvO:给定数据集D,假定其中有N个真实类别,将这N个类别进行两两配对(一个正类/一个反类),从而产生N(N-1)/2个二分类学习器,在测试阶段,将新样本放入所有的二分类学习器中测试,得出N(N-1)个结果,最终通过投票产生最终的分类结果。
优点:它在一定程度上规避了数据集 unbalance 的情况,性能相对稳定,并且需要训练的模型数虽然增多,但是每次训练时训练集的数量都降低很多,其训练效率会提高。
缺点:训练出更多的 Classifier,会影响预测时间。
-
OvM:给定数据集D,假定其中有N个真实类别,每次取出一个类作为正类,剩余的所有类别作为一个新的反类,从而产生N个二分类学习器,在测试阶段,得出N个结果,若仅有一个学习器预测为正类,则对应的类标作为最终分类结果。
优点:普适性还比较广,可以应用于能输出值或者概率的分类器,同时效率相对较好,有多少个类别就训练多少个分类器。
缺点:很容易造成训练集样本数量的不平衡(Unbalance),尤其在类别较多的情况下,经常容易出现正类样本的数量远远不及负类样本的数量,这样就会造成分类器的偏向性。
-
MvM:给定数据集D,假定其中有N个真实类别,每次取若干个类作为正类,若干个类作为反类(通过ECOC码给出,编码),若进行了M次划分,则生成了M个二分类学习器,在测试阶段(解码),得出M个结果组成一个新的码,最终通过计算海明/欧式距离选择距离最小的类别作为最终分类结果。
十一、逻辑回归实例(数据来源于Kaggle)
员工离职预测