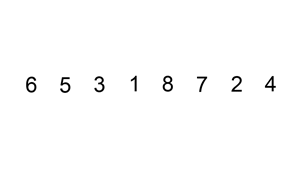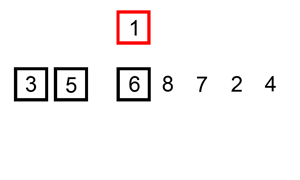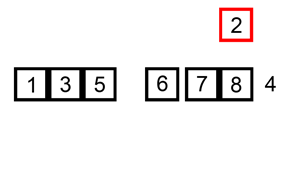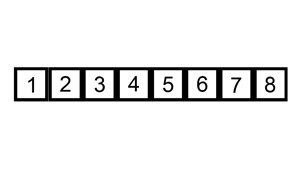我没有为这种算法做任何事,我的名字不应该出现在算法的名字中。---- 希尔(shell排序作者)
希尔排序按其设计者希尔(Donald Shell)的名字命名,该算法由1959年公布。一些老版本教科书和参考手册把该算法命名为Shell-Metzner,即包含Marlene Metzner Norton的名字,但是根据Metzner本人的说法,“我没有为这种算法做任何事,我的名字不应该出现在算法的名字中。”
----那时候的名人多谦虚.
第一.定义
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法**的:
1. 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
2. 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位.
第二: 插入排序
既然提到了插入排序, 就在此先了解一下插入排序; 它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
话说一图胜千言, 来一张个人认为最容易理解的图:
对上图解释一下:
1. 从第一个元素开始,该元素可以认为已经被排序;
2. 取出下一个元素, 与前边的元素对比, 直到找到大于等于前边的那个数字停止, 对比过得数字往后移动;
3. 将新元素插入到该位置,
直接上OC代码, 之后会随着希尔排序一块放在github上:
/**
* 插入排序
*/
- (void)algorithm_InsertSortWith:(NSMutableArray *)array{
//将第一个数字视为 基准, 所以 i 从 1 开始
for (int i = 1; i < array.count; i++) {
//待定位的数字
int temp = [array[i] intValue];
//每次都从上次定位好的数字的前一位开始对比, 一直往前找, 直到找到合适位置<大于等于前边那个数字>,
for (int j = i - 1; j >= 0 && temp < [array[j] intValue]; j --) {
//凡是不合格的数字都靠后移动
array[j + 1] = array[j];
//最终将合格的数字确定位置
array[j] = [NSNumber numberWithInt:temp];
}
}
NSLog(@"排序过后的数组为: %@", array);
}
第三. 分析
还是说希尔排序产生的缘由吧,
1. 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
2. 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位.
主要是和时间复杂度O(n²)过不去, 就是看你不顺眼.
聊天都离不开GIF, 这里怎么能少! 隔着GIF图就感觉到前辈们的牛逼气息!
希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。即: 可以将数据分区域放在一个二维数组中,每个区一列, 然后对每一列排序.
待排序数组---[9, 1, 5, 8, 3, 7, 4, 6, 2], 先将步长设置为3, 稍后看步长
例子一
第一次分组<步长==3>原始数据为[9, 1, 5, 8, 3, 7, 4, 6, 2]
9, 1, 5
8, 3, 7
4, 6, 2
第一次排序后为[4, 1, 2, 8, 3, 5, 9, 6, 7];
4, 1, 2
8, 3, 5
9, 6, 7
第二次分组<步长==2>原始数据为[4, 1, 2, 8, 3, 5, 9, 6, 7];
4, 1
2, 8
3, 5
9, 6
7
第二次排序后为[2, 1, 3, 5, 4, 6, 7, 8, 9];
2, 1
3, 5
4, 6
7, 8
9
第三次分组步长==1, 排序后为 [1, 2, 3, 4, 5, 6, 7, 8, 9]
例子二
以图片的形式展示以上的操作步骤:
重点---步长计算
通过以上的插入排序与希尔排序的例子, 想必对希尔排序有了初步的认识, 但对于步长这个东西完全模糊....放心;
因为步长的选择是希尔排序的重要部分, 所以摘出来单独说明; 作者最初的建议是折半再折半知道最后的步长为1<也就是插入排序>, 但是当用较小步长排序后,以前用的较大步长仍然是有序的。, 如果一个数列以步长5进行了排序然后再以步长3进行排序,那么该数列不仅是以步长3有序,而且是以步长5有序。如果不是这样,那么算法在迭代过程中会打乱以前的顺序,那就不会以如此短的时间完成排序了。 摘录自wiki百科
已知的最好步长序列是由Sedgewick提出的 **1,5,19,41,109,... **
它是由交错两个序列的元素获得:<公式: 9(4 ķ - 2 ķ)+ 1 和 2 K + 2(2 K + 2 - 3)+ 1 >
1,19,109,505,2161,... ...,|| 9(4 ķ - 2 ķ)+ 1,K = 0,1,2,3,...
5,41,209,929,3905,... ..|| 2 K + 2(2 K + 2 - 3)+ 1,K = 0,1,2,3,...
这项研究也表明“比较在希尔排序中是最主要的操作,而不是交换。”用这样步长序列的希尔排序比插入排序要快,甚至在小数组中比快速排序和堆排序还快,但是在涉及大量数据时希尔排序还是比快速排序慢。可以参考 Sorting Algorithms - Shellsort
OC希尔排序代码
- (void)algorithm_shellSortWith:(NSMutableArray *)array{
//总长度
int n = (int)array.count;
//最外层for循环确定----步长的个数 <折半直至为步长等于 1 >
for (int gap = n / 2; gap > 0; gap /= 2){
NSLog(@"步长----%d", gap);
//确定以步长为间隔的一对数字的后一个.
for (int i = gap; i < n; i++){
NSLog(@"第 %d 位 与第 %d 位对比", i - gap, i);
//找到成对的前一个, 加上判断<从第一位开始><升序降序>, j -= gap, 小组内排序
for (int j = i - gap; j >= 0 && array[j] > array[j + gap]; j -= gap){
![Uploading Sorting_shellsort_anim_123589.gif . . .]
//交换位置
[array exchangeObjectAtIndex:j withObjectAtIndex:(j + gap)];
}
}
}
NSLog(@"----%@", array);
}
还得在整理一下.....
参考链接
1. 维基百科
2. Sorting Algorithms - Shellsort
更多精彩内容请关注“IT实战联盟”哦~~~