实验六、数据挖掘之关联分析
一、实验目的
1. 理解Apriori算法的基本原理
2. 理解FP增长算法的基本原理
3. 学会用python实现Apriori算法
4. 学会用python实现FP增长算法
二、实验工具
1. Anaconda
2. sklearn
3. Pandas
三、实验简介
Apriori算法在发现关联规则领域具有很大影响力。算法命名源于算法使用了频繁项集性质的先验(prior)知识。在具体实验时,Apriori算法将发现关联规则的过程分为两个步骤:第一步通过迭代,检索出事务数据库中的所有频繁项集,即支持度不低于用户设定的阈值的项集;第二步利用频繁项集构造出满足用户最小信任度的规则。其中,挖掘或识别出所有频繁项集是该算法的核心,占整个计算量的大部分。
在对深度优先数据挖掘算法的研究工作中,Han等人没有采用潜在频繁项集的方法求解频繁项集,而是提出了称为频率模式增长(FP_growth)的算法。该算法通过扫描数据库创建FP_tree的根节点并标示为null,对数据库D中的每一个事务Tran,按L中的次序对Tran中的频繁项排序,设Tran中排序后的频繁项列表[p|P],这里p是第一个元素,P是保留列表。接着调用函数insert_tree([p|P],T),如果树T有一个子节点N且N.item_name=p.item_name,就将N节点计数加1;否则就创建一个新节点N,设计数为1,它的父节点连接到T,节点连接到同名的节点连接结构上。如果P是非空的,就递归调用insert_tree(P,N)。由于压缩了数据库内容,并且在将频繁项写入FP_tree结构时,保留了项集间的相连信息。求解频繁项集的问题,就转化为递归地找出最短频繁模式并连接其后缀构成长频繁模式的问题。
四、实验内容
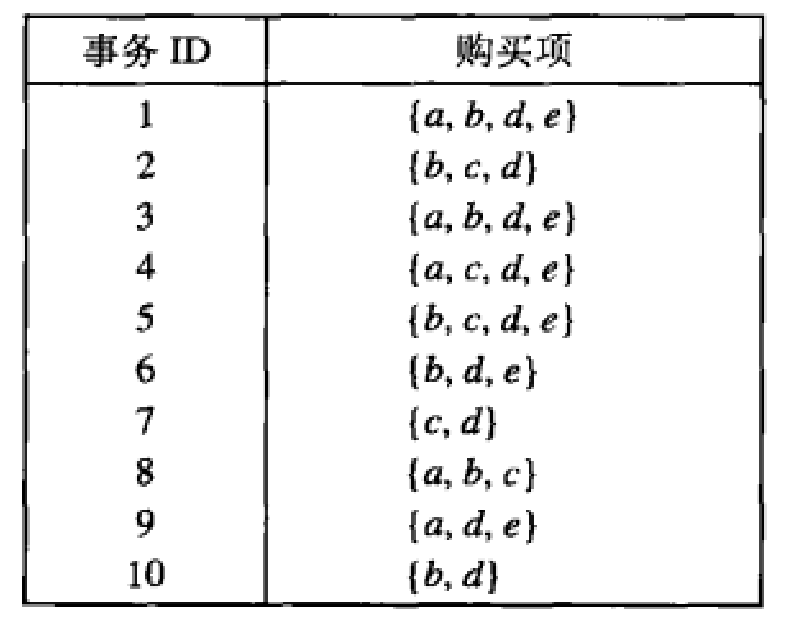
1. 利用python语言编写Apriori算法,挖掘出下表中数据集的频繁项集,最小支持度为30%。
def load_data_set(): data_set = [['a','b','d','e'], ['b', 'c', 'd'], ['a','b','d','e'], ['a','b','d','e'], ['a','b','d','e'], ['b', 'd', 'e'], ['c', 'd'], ['a', 'b', 'c'], ['a', 'd', 'e'], ['b', 'd']] return data_set def Create_C1(data_set): ''' 参数:数据库事务集 ''' C1 = set() for t in data_set: for item in t: item_set = frozenset([item]) # 为生成频繁项目集时扫描数据库时以提供issubset()功能 C1.add(item_set) return C1 def is_apriori(Ck_item, Lk_sub_1): ''' 参数:候选频繁k项集,频繁k-1项集 ''' for item in Ck_item: sub_item = Ck_item - frozenset([item]) if sub_item not in Lk_sub_1: return False return True def Create_Ck(Lk_sub_1, k): ''' # 参数:频繁k-1项集,当前要生成的候选频繁几项集 ''' Ck = set() len_Lk_sub_1 = len(Lk_sub_1) list_Lk_sub_1 = list(Lk_sub_1) for i in range(len_Lk_sub_1): #i: [0, len_Lk_sub_1) for j in range(i+1, len_Lk_sub_1): #j: [i+1, len_Lk_sub_1) l1 = list(list_Lk_sub_1[i]) l2 = list(list_Lk_sub_1[j]) l1.sort() l2.sort() # 判断l1的前k-1-1个元素与l2的前k-1-1个元素对应位是否全部相同 # list[s:t]:截取s到t范围的元素生成一个新list if l1[0:k-2] == l2[0:k-2]: Ck_item = list_Lk_sub_1[i] | list_Lk_sub_1[j] if is_apriori(Ck_item, Lk_sub_1): Ck.add(Ck_item) return Ck def Generate_Lk_By_Ck(data_set, Ck, min_support, support_data): ''' 参数:数据库事务集,候选频繁k项集,最小支持度,项目集-支持度dic ''' Lk = set() # 通过dic记录候选频繁k项集的事务支持个数 item_count = {} for t in data_set: for Ck_item in Ck: if Ck_item.issubset(t): if Ck_item not in item_count: item_count[Ck_item] = 1 else: item_count[Ck_item] += 1 data_num = float(len(data_set)) for item in item_count: if(item_count[item] / data_num) >= min_support: Lk.add(item) support_data[item] = item_count[item] / data_num return Lk def Generate_L(data_set, max_k, min_support): ''' 参数:数据库事务集,求的最高项目集为k项,最小支持度 ''' # 创建一个频繁项目集为key,其支持度为value的dic support_data = {} C1 = Create_C1(data_set) L1 = Generate_Lk_By_Ck(data_set, C1, min_support, support_data) Lk_sub_1 = L1.copy() # 对L1进行浅copy L = [] L.append(Lk_sub_1) # 末尾添加指定元素 for k in range(2, max_k+1): Ck = Create_Ck(Lk_sub_1, k) Lk = Generate_Lk_By_Ck(data_set, Ck, min_support, support_data) Lk_sub_1 = Lk.copy() L.append(Lk_sub_1) return L, support_data def Generate_Rule(L, support_data, min_confidence): ''' 参数:所有的频繁项目集,项目集-支持度dic,最小置信度 ''' rule_list = [] sub_set_list = [] for i in range(len(L)): for frequent_set in L[i]: for sub_set in sub_set_list: if sub_set.issubset(frequent_set): conf = support_data[frequent_set] / support_data[sub_set] # 将rule声明为tuple rule = (sub_set, frequent_set-sub_set, conf) if conf >= min_confidence and rule not in rule_list: rule_list.append(rule) sub_set_list.append(frequent_set) return rule_list if __name__ == "__main__": data_set = load_data_set() L, support_data = Generate_L(data_set, 4, 0.3)#最小支持度是30% rule_list = Generate_Rule(L, support_data, 0.7) for Lk in L: print("="*55) print("frequent " + str(len(list(Lk)[0])) + "-itemsets\t\tsupport") print("="*55) for frequent_set in Lk: print(frequent_set, support_data[frequent_set]) print() print("Rules") for item in rule_list: print(item[0], "=>", item[1], "'s conf: ", item[2])
2. (选做)利用python语言编写FP增长算法,挖掘出上表中数据集的频繁项集,最小支持度为30%。
五、实验总结(写出本次实验的收获,遇到的问题等)
通过本次实验的学习和编程,初步理解了Apriori算法的基本原理是使用频繁项集性质的先验性质,即频繁项集的所有非空子集也一定是频繁的。Apriori算法使用一种称为逐层搜索的迭代方法,其中k项集用于探索(k+1)项集。首先,通过扫描数据库,累计每个项的计数,并收集满足最小支持度的项,找出频繁1项集的集合。该集合记为L1。然后,使用L1找出频繁2项集的集合L2,使用L2找出L3,如此下去,直到不能再找到频繁k项集。每找出一个Lk需要一次数据库的完整扫描。Apriori算法使用频繁项集的先验性质来压缩搜索空间。
但是python编程能力薄弱,需要加强编程语言的学习才能更好的把算法真正实现出来,并进行频繁项集的输出。