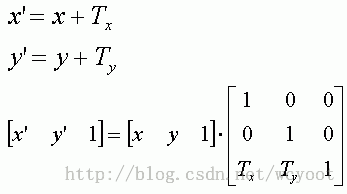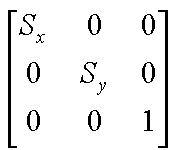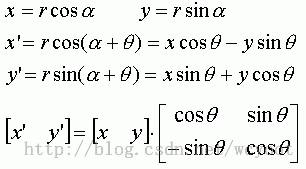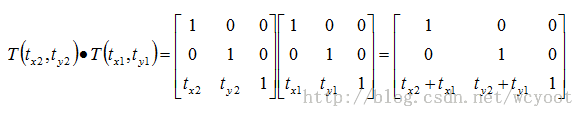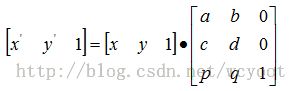第一次写ios相关技术博客,所以先写个简单的,写的不好大家多多提意见。
想学好这个类,我感觉最好还是从理论上弄明白什么二维图形到底是怎么变换的。
矩阵及其运算
一.数学概念
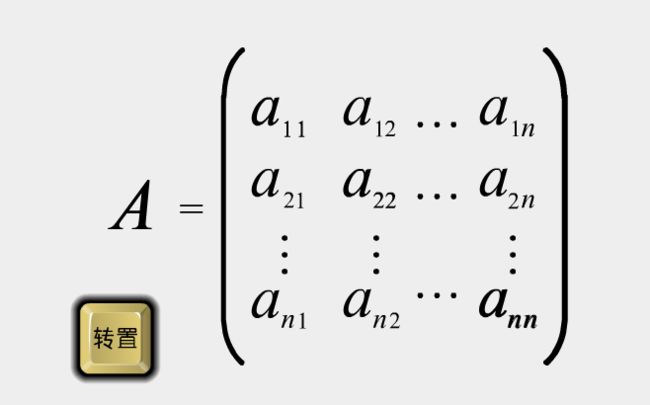
定义1.1 由!
个数
排成m行n列的数表
称为m行n列的矩阵,简称 矩阵,记作
二.原理,公式和法则
1.矩阵的加法
(1) 公式
(2) 运算律
2.数乘矩阵
(1) 公式
(2) 运算律
3.矩阵与矩阵相乘
, 则
,其中
,且
(2) 运算符(假设运算都是可行的):
(3) 方阵的运算
注意:①矩阵乘法一般不满足交换律。
4.矩阵的转置
(1) 公式
(2) 运算律
!
5.方阵的行列式
6.共轭矩阵
上面一定要看懂矩阵的乘法是怎么运算的才行。
数学原理
1、基本几何变换及变换矩阵
基本几何变换都是相对于坐标原点和坐标轴进行的几何变换,有平移、比例、旋转、反射和错切等
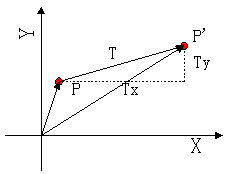
1.1 平移变换
是指将p点沿直线路径从一个坐标位置移到另一个坐标位置的重定位过程。他是一种不产生变形而移动物体的刚体变换(rigid-body transformation),如下图所示。
推导:
解释(个人理解)
x'=x+Tx 相当于x'= x*1 + y*0 + 1 * Tx
y'=y+Ty 相当于y'= x*0 + y*1 + 1 * Ty
所以 A 矩阵 [x y 1]
C 矩阵要和A矩阵格式一样 [x' y' 1]
c矩阵的1 怎么来。只能添加一行了
1=x*0+y*0+ 1*1
所以b矩阵为 上面如图
1.2 缩放变换
缩放变换是指对p点相对于坐标原点沿x方向放缩Sx倍,沿y方向放缩Sy倍。其中Sx和Sy称为缩放系数。
推导:
矩阵
x'=x*Sx+y*0 + 0*0;
y'=x*0 +y *Sy+0*0;
0=x*0+y*0+0*1;
缩放变换可改变物体的大小,如下图所示。当Sx=Sy >1时,图形沿两个坐标轴方向等比例放大;当Sx=Sy<1,图形沿两个坐标轴方向等比例缩小;当Sx≠Sy,图形沿两个坐标轴方向作非均匀的比例变换。
1.3 旋转变换
二维旋转是指将p点绕坐标原点转动某个角度(逆时针为正,顺时针为负)得到新的点p’的重定位过程。
[图片上传失败...(image-cbfe81-1535962641767)]
推导:利用极坐标方程
逆时针旋转θ角的矩阵如下:
1.4 对称变换
对称变换后的图形是原图形关于某一轴线或原点的镜像。
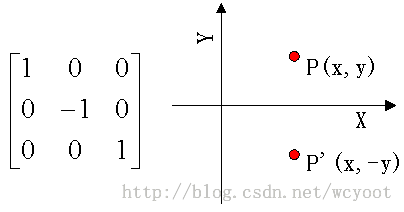
(1)关于x轴对称
x'=x*1+y*0+0*0;
y'=x*0+y*(-1)+0*0;
0=x*0+y*0+0*1;
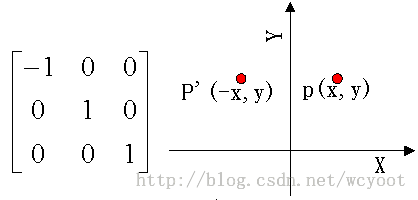
(2)关于y轴对称
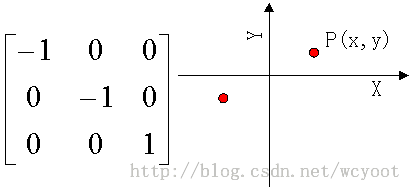
(3)关于原点对称
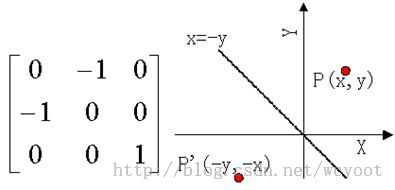
(4)关于y=x轴对称
(5)关于y=-x轴对称
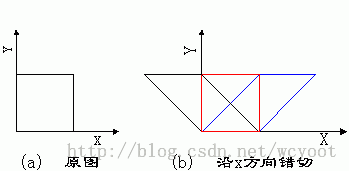
1.5 错切变换
错切变换也称为剪切、错位变换,用于产生弹性物体的变形处理。
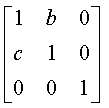
错切变换的变换矩阵为:
(1)沿x方向错切:b=0
(2)沿y方向错切:c=0
(3)两个方向错切:b和c都不等于0。
2、 复合变换
如果图形要做一次以上的几何变换,那么可以将各个变换矩阵综合起来进行一步到位的变换。复合变换有如下的性质:
1)复合平移
对同一图形做两次平移相当于将两次的平移两加起来:
2)复合缩放
两次连续的缩放相当于将缩放操作相乘:
3)复合旋转
两次连续的旋转相当于将两次的旋转角度相加:
缩放、旋转变换都与参考点有关,上面进行的各种变换都是以原点为参考点的。如果相对某个一般的参考点(xf,yf)作缩放、旋转变换,相当于将该点移到坐标原点处,然后进行缩放、旋转变换,最后将(xf,yf)点移回原来的位置。
4)关于(xf,yf)点的缩放变换
5)绕(xf,yf)点的旋转变换
3、二维图形几何变换的计算
几何变换均可表示成P’=P*T的形式
(1)点的变换:先将点表示为规范化齐次坐标形式,再乘以变换矩阵。
(2)直线的变换:将直线的两个端点表示为规范化齐次坐标形式,再乘以变换矩阵。
(3)多边形的变换:将多边形的顶点表示为规范化齐次坐标形式,再乘以变换矩阵。
(4)曲线的变换:将曲线的每个点表示为规范化齐次坐标形式,再乘以变换矩阵。
4、复合变换的矩阵点乘的先后问题
1)如果采用以下方式计算几何变换的变换矩阵
如上范例所示,其先执行变换的矩阵放在前面,后执行变换的矩阵放在后面。
2)如果采用以下方式计算几何变换的变换矩阵:
如上范例所示,其先执行变换的矩阵放在后面,后执行变换的矩阵放在前面。
这是因为矩阵的特性:CGAffineTransform.h 函数介绍
说了半天,不来点代码怎么行。
在CGAffineTransform.h 文件中
typedef struct CGAffineTransform CGAffineTransform;
struct CGAffineTransform {
CGFloat a, b, c, d;
CGFloat tx, ty;
};
矩阵数学模型是[a b]
c d
tx ty
省略了 [a b 0] 中的最后一列
c d 0
tx ty 1
函数介绍代码
///获取一个标准矩阵。没有变化的矩阵
CGAffineTransform transform= CGAffineTransformIdentity;
NSLog(@"CGAffineTransformIdentity 数值%@" , NSStringFromCGAffineTransform(transform));
///获取一个变幻矩阵 这个函数可以平移旋转和缩放
/* Return the transform [ a b c d tx ty ]. */
transform= CGAffineTransformMake(a, b, c, d,x,y);
///获取一个只做平移的矩阵
// t' = [ 1 0 0 1 tx ty ]
transform= CGAffineTransformMakeTranslation(x, y);
///获取一个缩放矩阵
// t' = [ sx 0 0 sy 0 0 ]
transform= CGAffineTransformMakeScale(a,c);
//获取一个旋转矩阵
/* Return a transform which rotates by `angle' radians:
t' = [ cos(angle) sin(angle) -sin(angle) cos(angle) 0 0 ] */
transform= CGAffineTransformMakeRotation(3);
///验证是否是标准矩阵
BOOL isTrue = CGAffineTransformIsIdentity(transform);
///这个是矩阵之间的换算了
/* Translate `t' by `(tx, ty)' and return the result:
t' = [ 1 0 0 1 tx ty ] * t */
/// 说的很明确 用只有平移的矩阵和 t 矩阵相乘 t*t' 意思是在t'的基础上做t 变幻(例如平移旋转等等)
transform= CGAffineTransformTranslate(transform,x,y);
///矩阵先缩放再transform
/* Scale `t' by `(sx, sy)' and return the result:
t' = [ sx 0 0 sy 0 0 ] * t */
transform= CGAffineTransformScale(transform,a,c);
///矩阵先旋转再transform
/* Rotate `t' by `angle' radians and return the result:
t' = [ cos(angle) sin(angle) -sin(angle) cos(angle) 0 0 ] * t */
transform = CGAffineTransformRotate(transform,3);
NSLog(@"CGAffineTransformInvert前 数值%@" , NSStringFromCGAffineTransform(transform));
/// 获取 反转矩阵 看不出效果。做图看看 可以仔细研究下
///我看着就是沿着y轴做了一个对称变换 (不见得对)
transform = CGAffineTransformInvert(transform);
NSLog(@"CGAffineTransformInvert后 数值%@" , NSStringFromCGAffineTransform(transform));
///矩阵相乘
/* Concatenate `t2' to `t1' and return the result:
t' = t1 * t2 */
transform = CGAffineTransformConcat(transform,transform);
///判断两个矩阵是否相等
/* Return true if `t1' and `t2' are equal, false otherwise. */
isTrue =CGAffineTransformEqualToTransform(transform,transform);
///获取一个点矩阵变幻另一个点的位置
/* Transform `point' by `t' and return the result:
p' = p * t
where p = [ x y 1 ]. */
CGPoint point= CGPointApplyAffineTransform(CGPointMake(30, 30), transform);
///获取一个矩形矩形变换的大小
/* Transform `size' by `t' and return the result:
s' = s * t
where s = [ width height 0 ]. */
CGSize size= CGSizeApplyAffineTransform(CGSizeMake(30, 30),transform);
///获取矩形位置变幻后的位置
CGRect rect=CGRectApplyAffineTransform(CGRectMake(0, 0, 30, 30),transform);
项目中有每个函数的具体用法。
项目托管在github
参考文章:
矩阵定义
变换原理
苹果官方文档