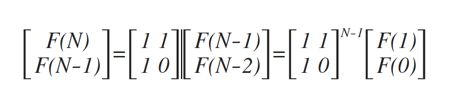面试算法代码知识梳理系列

面试算法知识梳理(1) - 排序算法
面试算法知识梳理(2) - 字符串算法第一部分
面试算法知识梳理(3) - 字符串算法第二部分
面试算法知识梳理(4) - 数组第一部分
面试算法知识梳理(5) - 数组第二部分
面试算法知识梳理(6) - 数组第三部分
面试算法知识梳理(7) - 数组第四部分
面试算法知识梳理(8) - 二分查找算法及其变型
面试算法知识梳理(9) - 链表算法第一部分
面试算法知识梳理(10) - 二叉查找树
面试算法知识梳理(11) - 二叉树算法第一部分
面试算法知识梳理(12) - 二叉树算法第二部分
面试算法知识梳理(13) - 二叉树算法第三部分

一、目录

斐波那契数列（循环算法、矩阵算法）
跳台阶问题
数值的整数次方
打印1到最大的n位数
计算从1到n中1出现的个数
求两个数的二进制表示中有多少个是不同的
给定一个整数N，求N!的末尾有多少个0
给定一个整数N，求N!的二进制表示中最低位1的位置
最大公约数
精确地表达有限/无限循环小数

二、代码实现

2.1 斐波那契数列（循环算法、矩阵算法）

问题描述

斐波那契数列满足下面的通项公式，要求给出N，输出第N项的F(N)

F(0)=0, F(1)=1, F(n)=F(n-1)+F(n-2)（n>=2，n∈N*）

解决思路

这里介绍两种解决办法，循环算法 和 矩阵算法。循环算法比较容易理解，就是从F(0)开始，根据通项公式，得到下一个斐波那契数列中的数字即可。

循环算法代码实现

class Untitled {
    
    static double fibonacci(int n) {
        if (n < 2) {
            return n;
        }
        //f(n-2)
        double fnMinus2 = 0;
        //f(n-1)
        double fnMinus1 = 1;
        double result = 0;
        for (int i=2; i<=n; i++) {
            //根据通项公式计算。
            result = fnMinus2 + fnMinus1;
            fnMinus2 = fnMinus1;
            fnMinus1 = result;
        }
        return result;
    }
    
    public static void main(String[] args) {
        double loopResult = fibonacci(10);
        System.out.println("loopResult=" + loopResult);
    }
}

循环算法运行结果

>> loopResult=55.0

矩阵算法解决思路

对于上面的通项公式，可以用下面的矩阵乘法的形式来表示

那么，我们的问题就变成了求该特殊矩阵的 N-1次方的值。

矩阵算法代码实现

class Untitled {
    
    static class Matrix {
        
        double a;
        double b;
        double c;
        double d;
        
        public Matrix(double a, double b, double c, double d) {
            this.a = a;
            this.b = b;
            this.c = c;
            this.d = d;
        }
    }
    
    //矩阵乘法函数。
    static Matrix multiMatrix(Matrix a, Matrix b) {
        Matrix result = new Matrix(0, 0, 0, 0);
        result.a = a.a*b.a + a.b*b.c;
        result.b = a.a*b.b + a.b*b.d;
        result.c = a.c*b.a + a.d*b.c;
        result.d = a.c*b.b + a.d*b.d;
        return result;
    }
    
    //核心函数。
    static double fibonacciMatrix(int n) {
        if (n < 2) {
            return n;
        }
        Matrix r = new Matrix(1, 0, 0, 1);
        Matrix tmp = new Matrix(1, 1, 1, 0);
        n--;
        while (n > 0) {
            if ((n&1) > 0) {
                r = multiMatrix(r, tmp);
            }
            tmp = multiMatrix(tmp, tmp);
            n >>= 1;
        }
        return r.a;
    }
    
    public static void main(String[] args) {
        double matrixResult = fibonacciMatrix(10);
        System.out.println("matrixResult=" + matrixResult);
    }
}

矩阵算法运行结果

>> matrixResult=55.0

2.2 跳台阶问题

问题描述

一个台阶总共有n级，如果一次可以跳1级，也可以跳2级，求总共有多少总跳法。

解决思路

由于有两种跳台阶方式，因此跳n级台阶可以转换为下面两个问题之和：

第一次跳1级台阶，之后的解法数为f(n-1)
第一次跳2级台阶，之后的解法数为f(n-2)

这就和之前的斐波那契数列的通项公式相同。

实现代码

class Untitled {

    static class Matrix {

        double a;
        double b;
        double c;
        double d;

        public Matrix(double a, double b, double c, double d) {
            this.a = a;
            this.b = b;
            this.c = c;
            this.d = d;
        }
    }

    //矩阵乘法函数。
    static Matrix multiMatrix(Matrix a, Matrix b) {
        Matrix result = new Matrix(0, 0, 0, 0);
        result.a = a.a*b.a + a.b*b.c;
        result.b = a.a*b.b + a.b*b.d;
        result.c = a.c*b.a + a.d*b.c;
        result.d = a.c*b.b + a.d*b.d;
        return result;
    }

    //核心函数。
    static double fibonacciMatrix(int n) {
        if (n < 2) {
            return n;
        }
        Matrix r = new Matrix(1, 0, 0, 1);
        Matrix tmp = new Matrix(1, 1, 1, 0);
        n--;
        while (n > 0) {
            if ((n&1) > 0) {
                r = multiMatrix(r, tmp);
            }
            tmp = multiMatrix(tmp, tmp);
            n >>= 1;
        }
        return r.a;
    }

    static double stepCounter(int step) {
        if (step <= 2) {
            return step;
        }
        return fibonacciMatrix(step);
    }


    public static void main(String[] args) {
        double count = stepCounter(50);
        System.out.println("counter=" + count);
    }
}

2.3 数值整数次方

实现代码

class Untitled {

    static double powerOfNum(int num, int power) {
        int tmp = num;
        int r = 1;
        while (power > 0) {
            //如果在该位上为1，那么就乘上对应的n次方。
            if ((power&1) > 0) {
                r = r*tmp;
            }
            tmp = tmp*tmp;
            power >>= 1;
        }
        return r;
    }


    public static void main(String[] args) {
        System.out.println("powerOfNum=" + powerOfNum(2, 10));
    }
}

运行结果

>> powerOfNum=1024.0

2.4 打印 1 到最大的 n 位数

class Untitled {

    static void printNumberCore(int p[], int depth, int len) {
        //到达末尾，打印当前数组中的元素。
        if (depth == len+1) {
            StringBuilder builder = new StringBuilder();
            for (int i=1; i<=len; i++) {
                builder.append(String.valueOf(p[i]));
            }
            System.out.println(builder.toString());
            return;
        }
        //如果是首位，那么从1开始，否则从0开始。
        int pStart = 0;
        if (depth == 1) {
            pStart = 1;
        }
        for (int i=pStart; i<=9; i++) {
            //替换该位，并进行递归。
            p[depth] = i;
            printNumberCore(p, depth+1, len);
        }
    }

    static void printNumber(int n) {
        //首先建立数组。
        int p[] = new int[n+1];
        //len表示有几位数。
        for (int len=1; len<=n; len++) {
            //对应于len位数的全排列。
            printNumberCore(p, 1, len);
        }
    }

    public static void main(String[] args) {
        printNumber(3);
    }
}

2.5 计算从 1 到 n 中 1 出现的个数

解决思路

这个问题，需要先总结一下规律，我们根据数字N的位数来进行分析：

一位数

那么N>=1时才会出现1，并且出现1的次数为1次

两位数

在这种情况下，出现1的次数等于个位上出现1的次数加上十位上出现1的个数。

个位上出现1的次数不仅和个位的数字有关，还和十位的数字有关：
- 如果个位为0，那么个位上出现1的次数等于十位的数字。
- 如果个位大于0，那么个位上出现1的次数等于十位的数字加1。
十位上出现1的次数不仅和十位的数字有关，还和个位的数字有关：
- 如果十位为1，那么十位上出现1的次数等于个位的数字加1。
- 如果十位大于1，那么十位上出现1的次数等于10。

N 位数

例如，如果要计算百位上1出现的次数，它要受到三方面的影响：百位上的数字，百位以下的数字，百位以上的数字。

如果百位上数字为0，百位上可能出现1的次数仅由更高位决定，等于更高位数字乘以当前位数。
如果百位上数字为1，百位上可能出现1的次数不仅受更高位影响还受低位影响：
- 受高位影响的部分等于更高位数字乘以当前位数
- 受低位影响等于低位数字加上1。
如果百位上数字大于1，则百位上出现1的情况仅由更高位决定，等于更高位数字加上1乘以当前位数。

代码实现

class Untitled {

    static int countOneNum(int data) {
        int iFac = 1;
        int countNum = 0;
        int lowNum = 0;
        int curNum = data % 10;
        int highNum = data / 10;
        //从个位数开始遍历，每次while循环向前移动一位，计算每一位出现1的次数，总和就是问题的解。
        while (curNum > 0 || highNum > 0) {
            if (curNum == 0) {
                countNum += highNum * iFac;
            } else if   (curNum == 1) {
                countNum += highNum * iFac + (lowNum + 1);
            } else {
                countNum += (highNum+1)*iFac;

            }
            lowNum = lowNum + curNum*iFac;
            curNum = highNum % 10;
            highNum = highNum / 10;
            iFac *= 10;
        }
        return countNum;
    }


    public static void main(String[] args) {
        System.out.println("n=" + 123 + ",result=" + countOneNum(123));
    }
}

运行结果

>> n=123,result=57

2.6 求两个数的二进制表示中有多少个是不同的

解决思路

对于一个二进制数，例如1010，将其减1后得到的结果是1001，也就是将最后一个1（倒数第二位）及其之后的0变成1，1变成0，再将该结果与原二进制数相与，也就是1010 & 1001 = 1000，那么就可以去掉最后一个1。

因此，如果需要计算两个数的二进制表示中有多少位是不同的，可以 先将这两个数异或，那么不相同的位数就会变成1，之后利用上面的技巧，通过每次去掉最后一个1，来 统计该结果中1的个数，就可以知道两个数的二进制表示中有多少是不同的了。

代码实现

class Untitled {

    static int getDiffBit(int a, int b) {
        int diff = a^b;
        int count = 0;
        while (diff > 0) {
            count++;
            diff = diff & (diff-1);
        }
        return count;
    }


    public static void main(String[] args) {
        System.out.println("result=" + getDiffBit(1999, 2299));
    }
}

运行结果

>> result=7

2.7 给定一个整数 N，求 N! 的末尾有多少个 0

问题描述

N!的含义为1*2*3*...*(N-1)*N，计算N!的十进制表示中，末尾有多少个0。

解答思路

N!中能产生末尾是0的质数组合是2*5，所以N!末尾的0的个数取决了2的个数和5的个数的最小值，有因为被2整除的数出现的概率大于5，因此5出现的次数就是N!末尾0的个数。因此，该问题就转换成为计算从1~N，每个数可以贡献5的个数，也就是每个数除以5的值。

上面的解法需要从1到N遍历每一个数，当然还有更加简便的方法。以26!为例，贡献5的数有5、10、15、20、25，一共贡献了6个5，可以理解为5的倍数5、10、15、20、25贡献了一个5，而25的倍数又贡献了一个5，得到下面的公式：

Z = [N/5] +[N/5^2] +[N/5^3] + …（总存在一个K，使得5^K > N，[N/5^K]=0）

代码实现

class Untitled {
    
    static int lowZeroN(int N) {
        int count = 0;
        while (N > 0) {
            N = N / 5;
            count = count + N;
        }
        return count;
    }
    
    public static void main(String[] args) {
        System.out.println("26!的十进制表示中末尾0的个数=" + lowZeroN(26));
    }
}

运行结果

>> 26!的十进制表示中末尾0的个数=6

2.8 给定一个整数 N，求 N! 的二进制表示中最低位 1 的位置

解答思路

首先，让我们换一个角度考虑，其实这个问题就是求解二进制表示中从最低位开始0的个数，因为二进制最低位为0代表的是偶数，能够被2整除，所以质因数2的个数就是二进制表示中最低位1后面的0的个数。

因此，我们的实现这就和上面2.7中求解质因数5的个数是一样的。

代码实现

class Untitled {
    
    static int lowOneN(int N) {
        int count = 0;
        while (N > 0) {
            N = N >> 1;
            count = count + N;
        }
        return count+1;
    }
    
    public static void main(String[] args) {
        System.out.println("3!的二进制表示中最低位1的位置=" + lowOneN(3));
    }
}

运行结果

>> 3!的二进制表示中最低位1的位置=2

2.9 最大公约数

问题描述

最大公约数的定义为 两个或多个整数的共有约数中最大的一个。这里采用的是更相止损法，其操作步骤为：

第一步：任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步。
第二步：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。

则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。

代码实现

class Untitled {

    static int gcd(int big, int small) {
        int fac = 1;
        int temp;
        while (small > 0) {
            //保证数字的先后顺序。
            if (small > big) {
                temp = big;
                big = small;
                small = temp;
            }
            if ((big & 1) > 0) {
                //奇奇。
                if ((small & 1) > 0) {
                    temp = big;
                    big = small;
                    small = temp - small;
                //奇偶。
                } else {
                    small >>= 1;
                }
            } else {
                //偶奇。
                if ((small & 1) > 0) {
                    big >>= 1;
                //偶偶。
                } else {
                    small >>= 1;
                    big >>= 1;
                    fac *= 2;
                }
            }
        }
        return big * fac;
    }


    public static void main(String[] args) {
        int result = gcd(319, 377);
        System.out.println("result=" + result);
    }
}

运行结果

>> result=29

2.10 精确地表达有限/无限循环小数

问题描述

有限小数或者无限循环小数都可以转化为分数，例如：

有限小数：0.9 = 9/10
无限循环小数：0.333（3）= 1/3

解决思路

在 http://blog.csdn.net/flyfish1986/article/details/47783545 这边文章中，详细地描述了该题的解决思路，核心思想就是将原小数分为 有限部分 和 无限循环小数 部分，对于这两部分别进行处理。

算法核心思想

代码实现

class Untitled {

    public static class Fraction {
        //分子。
        public double numerator;
        //分母。
        public double denominator;
    }

    public static double powerOf(int num, int mi) {
        double temp = 10;
        double result = 1;
        while (mi > 0) {
            if ((mi & 1) > 0) {
                result = result * temp;
            }
            temp = temp * temp;
            mi >>= 1;
        }
        return result;
    }

    //分为有限循环和无限循环两个部分，按照公式计算。
    public static Fraction getDescription(int limit, int limitLen, int unLimit, int unLimitLen) {
        //分别计算对应长度的10的n/m次幂。
        double limitPower = powerOf(10, limitLen);
        double unLimitPower = powerOf(10, unLimitLen);
        Fraction fraction = new Fraction();
        //根据公式计算分子和分母即可。
        fraction.numerator = limit * (unLimitPower - 1) + unLimit;
        fraction.denominator = (unLimitPower - 1) * limitPower;
        return fraction;
    }

    public static void main(String[] args) {
        Fraction f = getDescription(285714, 6, 285714, 6);
        System.out.println("res= " + f.numerator + "/" + f.denominator);
    }
}

运行结果

>> res= 2.85714E11/9.99999E11

面试算法知识梳理(14) - 数字算法

面试算法代码知识梳理系列

一、目录

二、代码实现

2.1 斐波那契数列（循环算法、矩阵算法）

问题描述

解决思路

循环算法代码实现

循环算法运行结果

矩阵算法解决思路

矩阵算法代码实现

矩阵算法运行结果

2.2 跳台阶问题

问题描述

解决思路

实现代码

2.3 数值整数次方

实现代码

运行结果

2.4 打印 1 到最大的 n 位数

2.5 计算从 1 到 n 中 1 出现的个数

解决思路

一位数

两位数

N 位数

代码实现

运行结果

2.6 求两个数的二进制表示中有多少个是不同的

解决思路

代码实现

运行结果

2.7 给定一个整数 N，求 N! 的末尾有多少个 0

问题描述

解答思路

代码实现

运行结果

2.8 给定一个整数 N，求 N! 的二进制表示中最低位 1 的位置

解答思路

代码实现

运行结果

2.9 最大公约数

问题描述

代码实现

运行结果

2.10 精确地表达有限/无限循环小数

问题描述

解决思路

代码实现

运行结果

更多文章，欢迎访问我的 Android 知识梳理系列：

你可能感兴趣的:(面试算法知识梳理(14) - 数字算法)