在介绍MPT树之前,先介绍一下比特币使用的Merkle树吧。
Merkle树很好理解,它将一个区块中的每一笔交易,都做一个double-SHA256(两次SHA256)操作,保存为叶子节点。
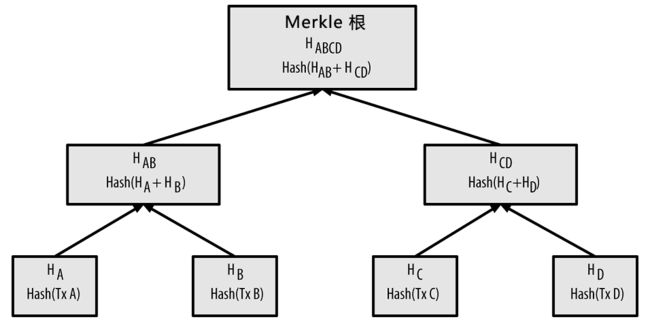
举个例子,如果现在有四个叶子节点,分别是HA、HB、HC和HD:
H~A~ = SHA256(SHA256(交易A))
通过串联相邻叶子节点的哈希值然后哈希之,这对叶子节点随后被归纳为父节点。 例如,为了创建父节点HAB,子节点A和子节点B的两个32字节的哈希值将被串联成64字节的字符串。随后将字符串进行两次哈希来产生父节点的哈希值:
H~AB~=SHA256(SHA256(H~A~ + H~B~))
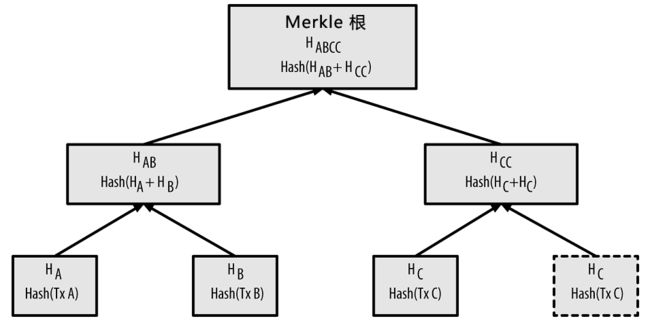
如果是奇数,那么就复制最后一个交易,组成一个平衡二叉树。如下图所示。
Merkle根的作用是为了证明区块中存在某个特定的交易。这样,一个节点只需要计算log2(N)个32字节的哈希值,形成一条从特定交易到树根的认证路径或者Merkle路径即可。这比遍历整个区块查找交易的速度要块的多,特别是如果一个区块中交易数量过大,计算量的减少会特别明显。因为相对于交易数量的增长,以基底为2的交易数量的对数的增长会缓慢许多。这使得比特币节点能够高效地产生一条10或者12个哈希值(320-384字节)的路径,来证明了在一个巨量字节大小的区块中上千交易中的某笔交易的存在。
Merkle树被SPV节点广泛使用。SPV节点不保存所有交易也不会下载整个区块,仅仅保存区块头。它们使用认证路径或者Merkle路径来验证交易存在于区块中,而不必下载区块中所有交易。
例如,一个SPV节点欲知它钱包中某个比特币地址即将到达的支付,该节点会在节点间的通信链接上建立起bloom过滤器,限制只接受含有目标比特币地址的交易。当节点探测到某交易符合bloom过滤器,它将以Merkleblock消息的形式发送该区块。Merkleblock消息包含区块头和一条连接目标交易与Merkle根的Merkle路径。SPV节点能够使用该路径找到与该交易相关的区块,进而验证对应区块中该交易的有无。SPV节点同时也使用区块头去关联区块和区块链中的区域区块。这两种关联,交易与区块、区块和区块链,证明交易存在于区块链。简而言之,SPV节点会收到少于1KB的有关区块头和Merkle路径的数据,其数据量比一个完整的区块(目前大约有1MB)少了一千倍有余。
Patricia Trie
Trie是一种字典树,用于存储文本字符,并利用了单词之间共享前缀的特点,所以叫做前缀树。不像平衡BST,Trie的高度只与最长的文本串的长度s有关系,而与单词的数量n无关。Trie的节点分两种:内部结点和叶子结点,内部结点用来存储单词key的成分字母,如果设字母表大小为d,那么每个内部结点最多有d个孩子,叶子结点存储该单词作为key的数据内容(data)。注意内部结点和叶子结点并不是互斥的,一个内部结点本身可以有儿子结点,同时它也可以是一个叶子结点。
如果一颗Trie中有很多单词只有一个儿子结点,可以用Patricia Trie(Linux内核中叫做Radix Tree)压缩存储。
第一部分 介绍
以太坊区块包括一个区块头,一个交易的列表和一个uncle区块的列表。
以太坊的每一个区块头,并非只包含一颗Merkle树,而是包含了三颗Merkle树,分别对应了三种对象:
1. 交易(Transactions)
2. 收据(Receipts,基本上,它是展示每一笔交易影响的数据条)
3. 状态(State)
现在先只看transaction的merkle树。在区块头部包括了交易的hash树根,用来校验交易的列表。在p2p网络上传输的是交易列表,这个交易列表被组装成一个叫做trie树的特殊数据结构,用以计算根hash。这个交易结构只用来校验区块,校验完就没用了。但是,这个交易结构会保存在本地,序列化成一个列表,当有客户端请求的时候,就发给它。这样,客户端就可以重构trie,校验每个区块的根hash。
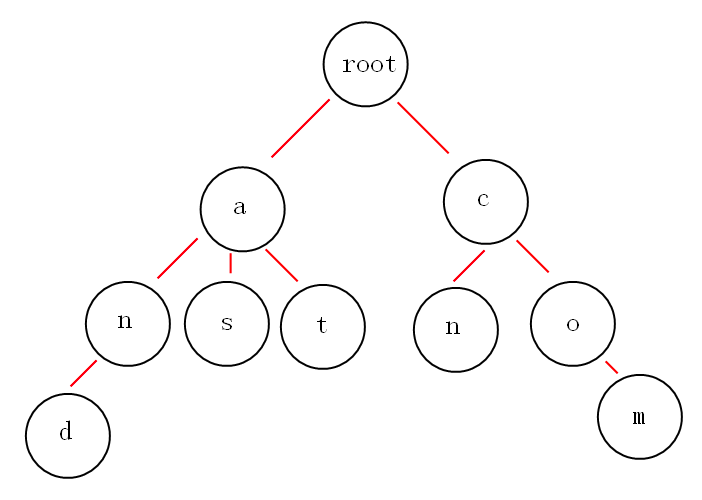
在普通的radix树中,key是从树根到value的真实的路径。即从根节点开始,key中的每个字符会标识走那个子节点从而到达相应value。Value被存储在每条路径终点的叶子节点。假如key来自一个包含N个字符的字母表,那么树中的每个节点都可能会有多达N个孩子,树的最大深度是key的最大长度。
简单地说,看下图的Trie树里,key是“com”,那么value就是右下角的叶子节点;key如果是“and”,那么value就是左下角的叶子节点。最长的key是com和and,所以这个树的最大深度是也就是3。
第二部分 普通Radix的优点
1.具有相同前缀的key所对应的value在树中很近。比如现在有understand和undergo这两个key。它们的叶子节点会很近,这样在访问的时候会节约时间和空间。
2.trie中不会有像hash-table一样的key值冲突。(我还不知道咋回事)
缺点:
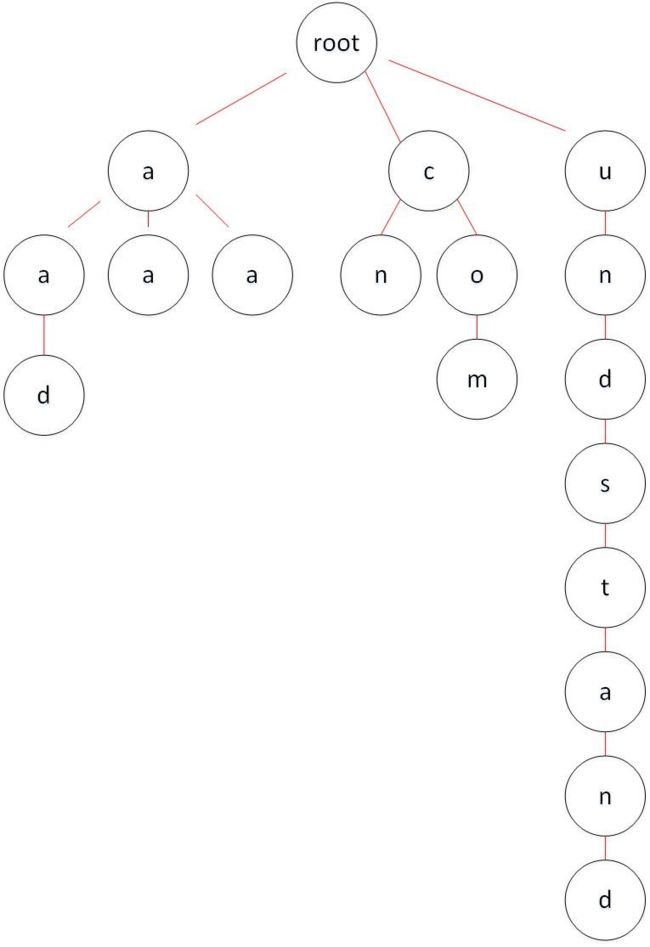
可能会非常低效。假如有一个很长的key,而且前缀也和其他的key都不同。那么在遍历或存储它对应的值得时候,你就会遍历(并存储)相当多的节点,尽管这个路径上没有其他value。因为这棵树可能是非常不平衡的。如下图中undstand这条路径所示。(极端一点,如果只要保存一个key为几百个字节长的[key,value],我们需要额外建立上千字节的空间,建立这么一层一层的树,每次查看和删除,都有几百步。为了解决这个问题引入了Patricia Tree)
第三部分 以太坊的改进
以太坊的方法就是一个编码方法。
1.为了保证树的达到密码学的安全标准。在leveldb数据库中,想要引用节点,就使用本节点的hash(我理解的就是key值是节点hash)。根节点就是整个数据结构的加密指纹。
2.为了提高效率,增加了很多不同的节点“类型”:
(1)空节点(blank node,NULL),空字符串
(2)标准叶子节点(standard leaf
node,aka kv node),这个节点里面是一个两项的[key,value]的数组,这些节点组成一个标准的[key,value]列表。
(3)扩展节点(extension node),这些节点也保存一个标准的[key,value]列表。不同之处在于它们的value是其他节点的hash,通过这个hash可以在数据库里找到这个节点。
(4)分支节点(branch node),这些节点保存一个17个元素长的数组([ v0 ... v15, vt ])。前16个字节对应了一个key中16个可能的十六进制字符;而最后一个字节是这样的:如果有一个[key,value]在这个分支节点终止时,最后一个字节会保存一个value。如果你搞不懂,没关系,谁也搞不懂。一会看下面的例子就明白了。
3.key使用特殊的十六进制前缀(hex-prefix,
HP)编码。
传统的十六进制字符串编码的压缩方式,是把它转化成十进制的。比如把12e4d8保存为\x12\xe4\xd8这样。但是如果这个十六进制字符串长度是个偶数可咋整?
由于字母表是16进制的,所以每个节点可能有16个孩子。因为有两种[key,value]节点(标准叶子节点和扩展节点),所以以太坊使用一个“terminator flag”来区分两种节点。如果terminator flag打开,那么key指向一个标准叶子节点,对应的value就是这个key的value;如果terminator
flag关闭,那么key指向扩展节点,这个节点中的value值就是用于在数据库中查询对应的节点的hash。无论key长度是奇数还是偶数,HP都可以对其进行编码。最后,注意,一个单独的十六进制字符或者4bit二进制数字,也就是我们说的一个半字节(nibble)。
HP编码很简单,主要作用就是解决奇数个十六进制位的问题。在key后加一个半字节,对terminator flag的状态和奇偶性进行编码。最低位表示奇偶性,第二低位编码terminator flag状态。如果key长度是偶数,就要再加上另外一个值为0的半字节,保持整体的偶特性(这样就可以按字节表示了)。
举例!
四个[key,value]对: ('dog','puppy'), ('horse', 'stallion'), ('do', 'verb'), ('doge', 'coin')
[ 6, 4, 6, 15, 16 ] : 'verb'
[ 6, 4, 6, 15, 6, 7, 16 ] : 'puppy'
[ 6, 4, 6, 15, 6, 7, 6, 5, 16 ] : 'coin'
[ 6, 8, 6, 15, 7, 2, 7, 3, 6, 5, 16 ] : 'stallion'
解释一下,左边是key的值,右边是value
d=0x64, o=0x6f,g=0x67,e=0x65,最后的16是0x10。
同理,下面的h= 0x68, o=0x6f, r=0x72, s=0x73, e=0x65
生成树:
ROOT: [ '\x16', A ]
A: [ '', '', '', '', B, '', '', '', C, '', '', '', '', '', '', '', '' ]
B: [ '\x00\x6f', D ]
D: [ '', '', '', '', '', '', E, '', '', '', '', '', '', '', '', '', 'verb' ]
E: [ '\x17', F ]
F: [ '', '', '', '', '', '', G, '', '', '', '', '', '', '', '', '', 'puppy' ]
G: [ '\x35', 'coin' ]
C: [ '\x20\x6f\x72\x73\x65', 'stallion' ]
再解释一下,这里的ROOT是根节点,所有的''都是空节点。
A、D、F是分支节点。
B、E是扩展节点。
C、G是标准叶子节点。
下面是编码详细介绍:
ROOT:扩展节点。0x16,1代表是奇偶性为奇,6是真正的前缀。
A:分支节点。第5个是B,第9个是C(从0开始数,分别是4和8)。所以B的key前缀以0x64开头,C的key以0x68开头(加上扩展节点中的6)。
B:扩展节点。0x006f,前面的0x00代表奇偶性为偶,且节点为扩展节点。6f是前缀的一部分。D的key前缀以0x64 6f开头
D:分支节点,有value的那种。第17个元素'verb'是value。第7个为E。所以E的前缀是0x646f6。
E:扩展节点。0x17,1代表奇偶性为奇,且节点为7是前缀的一部分。E这条路径已经走到了0x64 6f 67.
F:分支节点,有value的那种。第17个元素'puppy'是value。第7个为G,所以G的key前缀是0x64 6f 67 6.
G:标准叶子节点。0x35,3表示奇偶性为奇,且节点为标准叶子节点。5是key的前缀的一部分。G这条路经0x646f 67 65
C:标准叶子节点。0x20,2表示奇偶性为偶,且节点为标准叶子节点。后面的0x6f 72 73 65都是前缀。这边就很简单,ROOT上key的公有前缀是6,根据A节点中C的位置判断,key前缀是0x68.根据C自己这个前缀,C的key为0x68 6f 72 73 65
疑问:最后的16 是哪里来的?!
总结:总的来说,以太坊中的MTP树是比特币中Merkle Tree和Radix Tree(Trie)的混编版。MPT树能有效减少Trie树的深度,增加Trie树的平衡性。而且通过节点的hash值进行树的节点的链接,有助于提高树的安全性和可验证性。所以说MPT树是Trie和Merkle树混合加上平衡操作后的产物。
references:
《精通比特币》
《谈谈以太坊的Merkle树》,http://www.bitabc.com/?id=169
ethereum wiki:https://github.com/ethereum/wiki/wiki/Patricia-Tree
《Merkle Patricia Tree (MPT) 树详解》:http://www.cnblogs.com/fengzhiwu/p/5584809.html 这篇文章翻译自:https://easythereentropy.wordpress.com/2014/06/04/understanding-the-ethereum-trie/ 但是翻译的不好。